CS285 Lecture15&16 Offline Reinforcement Learning

Overview#

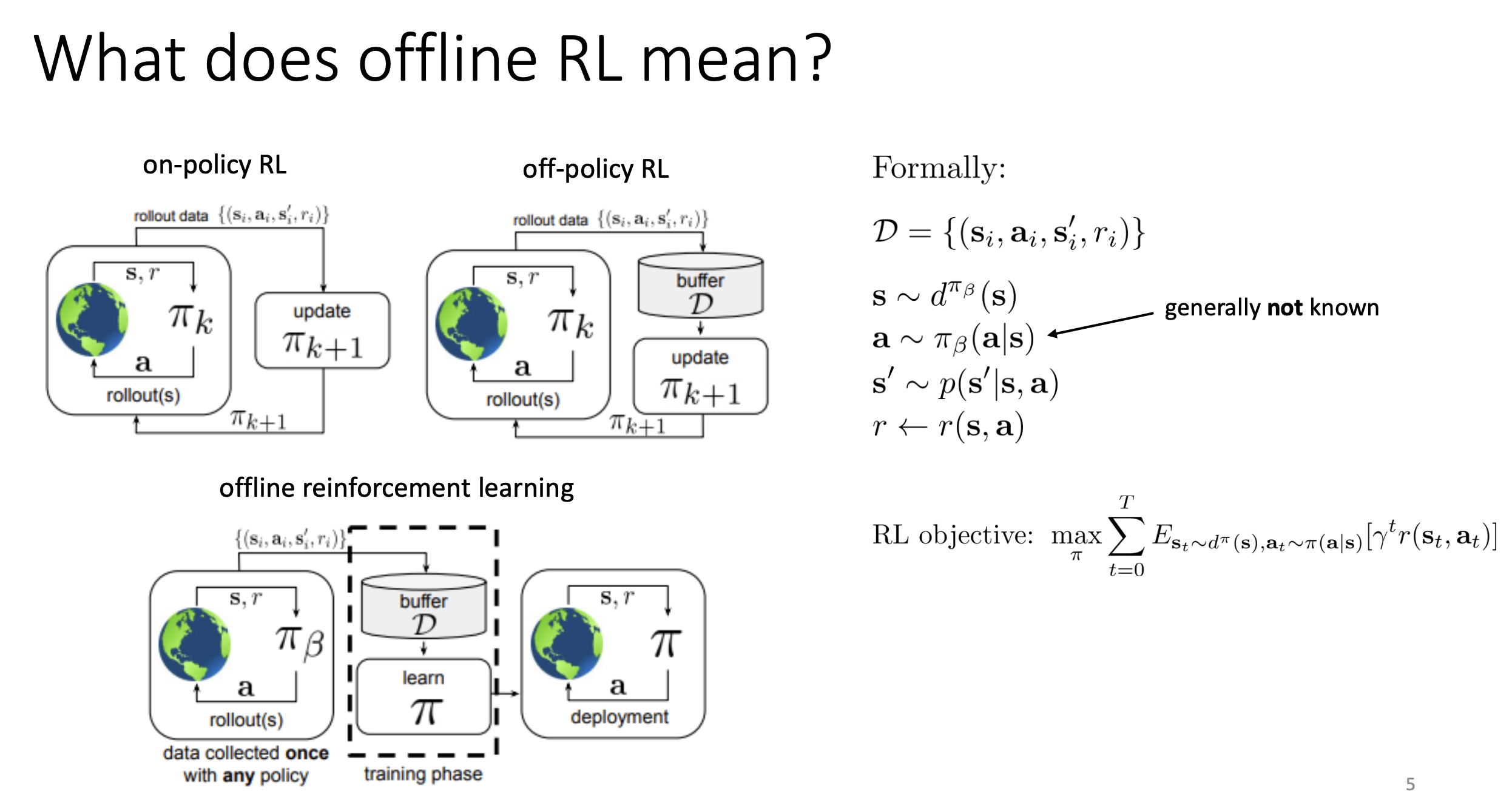
这一章讲的是offline RL，主要想法就是之前RL算法都要让policy部署到新的环境来尝试从而进行不断的训练。但是有的场景可能并不能承受住模型的尝试，比如说医疗场景。那offline Rl解决的问题就是给定一个未知policy收集到的数据集，然后只在这个数据集上面来训练我的模型。

那么我们想要的这个策略应该符合一些直觉，我们想要的模型不应该是跟模仿学习一样的，我们不只是先要模仿给定的数据集中的行动。我们想要从中学习到好的动作，从给定的数据集中整理出什么是好的动作，什么是不好的，从而得到比数据集中的数据更好的策略。

Problem#

但是直接在离线的数据集上用Q-learning会有一些问题

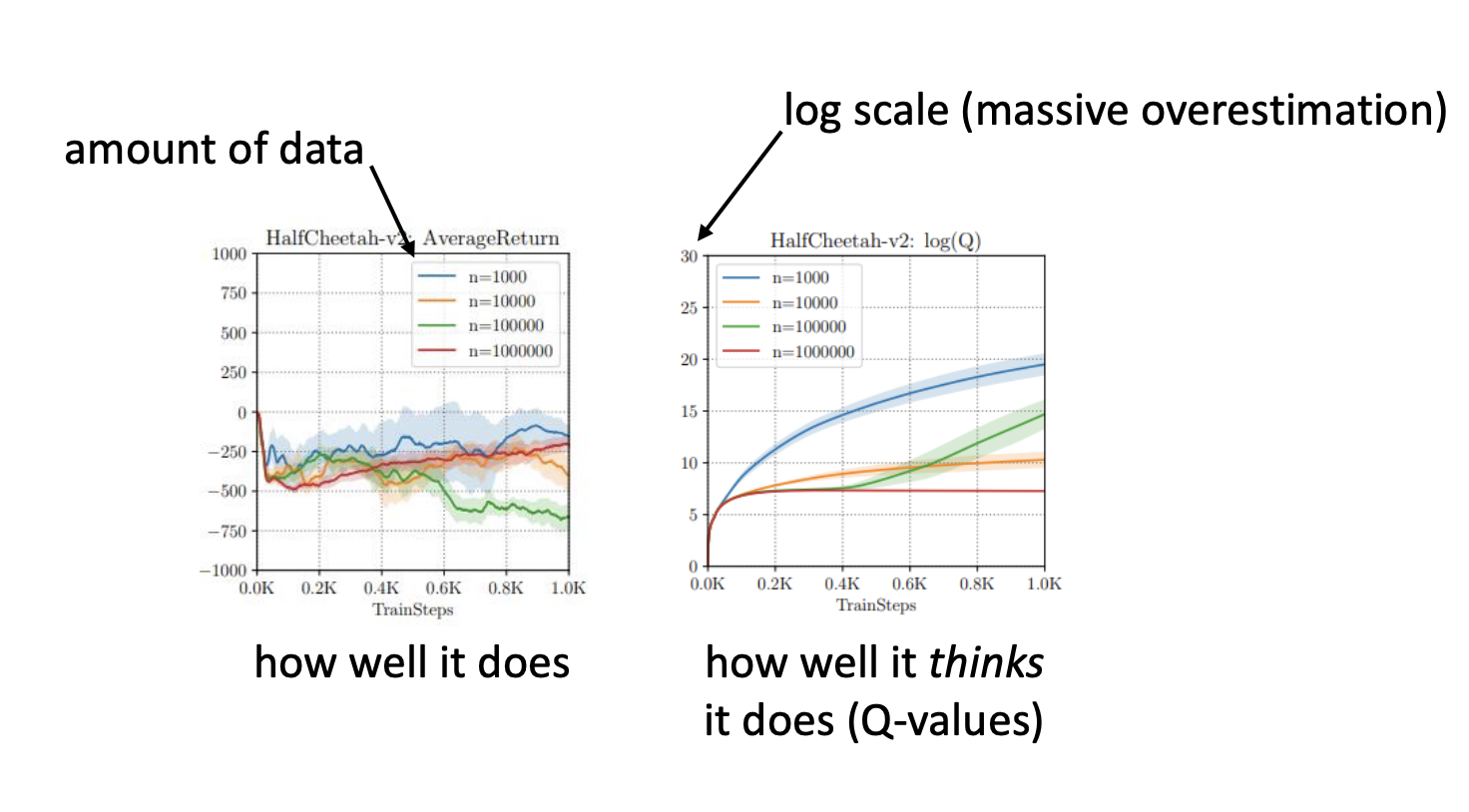
• 左图 (AverageReturn): 随着训练步数（TrainSteps）增加，智能体在实际环境中的表现（平均回报）不仅没有变好，反而急剧下降，甚至跌至负值。这代表“它实际做得有多差” (how well it does) 。
• 右图 (log(Q)): 与此同时，Q 值（对数坐标）却在呈指数级上升（爆炸）。这意味着智能体认为自己会获得天文数字般的回报。这代表“它以为自己做得有多好” (how well it thinks it does)

为什么呢？ 因为标准 Q-learning 的更新公式： 在 Q-learning 中，我们使用以下目标来更新 Q 值：

$$Q(s,a) \leftarrow r(s,a) + E_{a' \sim \pi_{new}}[Q(s',a')]$$

其中，新策略 $\pi_{new}$ 通常是贪婪策略，即去选择那个让 Q 值最大的动作：

$$\pi_{new} = \arg \max_{\pi} E_{a \sim \pi(a|s)}[Q(s,a)]$$

• 分布偏移 (Distribution Shift)： 在离线设置中，我们只能看到行为策略 $\pi_{\beta}$（产生数据的策略）所覆盖的动作。对于未见过的动作（OOD actions），Q 网络（神经网络）的预测是未定义的，可能会有很大的误差（噪声）。
• 最大化带来的问题 (The Maximization Bias)： 当你执行 $\arg \max$ 操作时，你实际上是在“寻找” Q 值最高的地方。
  • 如果 Q 函数在 OOD 区域恰好有正向的误差（预测值偏高），最大化操作就会直接选中这些动作 。 如果你去优化一个拟合好的函数 $x^* \leftarrow \arg \max_x f_{\theta}(x)$，而 $x$ 超出了训练数据的范围，你往往会利用模型的误差，找到一个虚假的“伪高点” 。

这个问题在之前的off policy中也有，解决办法就是 为了防止新学习的策略 $\pi_{new}$ 偏离数据分布太远（从而进入 Q 值估计不准的区域），我们在更新策略时增加一个约束条件：

$$\pi_{new}(a|s) = \arg \max_{\pi} E_{a \sim \pi(a|s)}[Q(s,a)] \quad \text{s.t.} \quad D_{KL}(\pi || \pi_{\beta}) \le \epsilon$$

• 含义： 我们依然希望最大化 Q 值，但是我们要求新策略 $\pi$ 和行为策略 $\pi_{\beta}$（即产生数据的策略）之间的差异（由 KL 散度衡量）不能超过 $\epsilon$。
• 目的： 确保新策略只在数据覆盖的范围内进行优化，从而避免查询到那些 Q 值可能极其错误的未见动作（OOD actions）。

虽然这个想法听起来很合理，但是有两个主要问题：

• 问题 1：我们通常不知道行为策略 $\pi_{\beta}(a|s)$
  • 在离线 RL 中，数据集可能来源复杂，例如：
    • 人类提供的演示数据 。
    • 手工设计的控制器 。
    • 过去多次 RL 实验混合的数据 。
  • 在这些情况下，没有一个明确的数学公式来表示 $\pi_{\beta}$，因此很难直接计算 KL 散度。
• 问题 2：这种约束既“太悲观”又“不够悲观”
  • 太悲观（Too pessimistic）： 即使在某些区域 Q 值估计是准确的，KL 约束也会强行把策略拉回行为策略，限制了改进空间。
  • 不够悲观（Not pessimistic enough）： 单纯的 KL 散度可能无法精准地剔除那些 Q 值特别离谱的特定动作，或者如果 $\pi_{\beta}$ 本身覆盖面很广但数据稀疏，KL 约束可能不足以保证安全。

既然我们要限制新策略 $\pi$ 不偏离行为策略 $\pi_{\beta}$，我们具体应该用什么样的数学形式来实现这种限制？

1. KL 散度 (KL-divergence)

$$D_{KL}(\pi || \pi_{\beta})$$

这种方法要求新策略 $\pi$ 和行为策略 $\pi_{\beta}$ 的分布形状尽可能相似。

• 优点 (+)： 非常容易实现（Easy to implement）
• 缺点 (-)： 这不一定是我们真正想要的（Not necessarily what we want）。
  • 原因解析：如上图所示，KL 散度会惩罚两个分布之间的差异。为了权衡KL散度，和Q value，KL散度得出来的policy可能就是浅绿色的$\pi$ ，但是这个策略同样给了一些不好的动作相对较高的可能性。实际上深绿色的那条线可能会更好，但是因为KL散度我们得不出来

2. 支持集约束 (Support Constraint)

$$\pi(a|s) \ge 0 \text{ only if } \pi_{\beta}(a|s) \ge \epsilon$$

这种方法只要求：只要 $\pi_{\beta}$ 在某个动作上的概率大于一个阈值 $\epsilon$（即数据中存在该动作），$\pi$ 就可以选这个动作。

• 含义：他要求 $\pi$尽量不要跑到坏数据的地方去。
• 优点 (+)： 这更接近我们真正想要的（Much closer to what we really want），即在保证安全（有数据支持）的前提下，最大化 Q 值。
• 缺点 (-)： 实现起来极其复杂（Significantly more complex to implement）。因为在连续动作空间中，很难硬性定义“支持集”的边界。

隐式策略约束方法（Implicit Policy Constraint Methods）#

出发点依然是我们之前定义的那个带约束的优化问题 ：

$$\pi_{new}(a|s) = \arg \max_{\pi} E_{a \sim \pi(a|s)}[Q(s,a)] \quad \text{s.t.} \quad D_{KL}(\pi || \pi_{\beta}) \le \epsilon$$

即：在不偏离行为策略 $\pi_{\beta}$ 太远的前提下，最大化 Q 值。

上述问题实际上是一个经典的凸优化问题。通过使用拉格朗日乘子法（Lagrange Multipliers） 和对偶性（Duality），我们可以直接推导出最优策略 $\pi^*$ 的数学形式 2：

$$\pi^*(a|s) = \frac{1}{Z(s)} \pi_{\beta}(a|s) \exp\left(\frac{1}{\lambda} A^{\pi}(s,a)\right)$$

• $\pi_{\beta}(a|s)$：原本的数据分布（行为策略）。
• $\exp(\dots)$：指数项，用于调整概率。
• $A^{\pi}(s,a)$：优势函数（Advantage Function），表示动作 $a$ 比平均水平好多少。
• $\lambda$：拉格朗日乘子（温度参数），控制约束的强弱。
• $Z(s)$：归一化常数（Partition Function），确保概率之和为 。

直观理解： 最优策略其实就是把原来的数据分布 $\pi_{\beta}$ 进行“重新加权”（Re-weighting）。

• 如果某个动作的优势 $A(s,a)$ 很大（Q 值很高），它的权重就会通过 $\exp$ 函数指数级增加。
• 如果优势很小或为负，权重就降低。
• $\pi^*$ 依然是在 $\pi_{\beta}$ 的支撑集（Support）内，只是把概率密度向高价值动作倾斜了。

但是这公式仍然要求我们知道$\pi_{\beta}$ ,于是我们可以用采样，从给定的数据集中采样 这可以通过加权最大似然估计（Weighted Maximum Likelihood Estimation） 来实现：

$$\pi_{new} = \arg \max_{\pi} E_{(s,a) \sim \pi_{\beta}} \left[ \log \pi(a|s) \cdot \exp\left(\frac{1}{\lambda} A^{\pi_{old}}(s,a)\right) \right]$$

这个方法中，我们用加权回归更新了策略 $\pi$，这确实避免了策略训练时的 OOD 问题。但是，第给出的 Critic（Q 函数）的损失函数：

$$\mathcal{L}_C(\phi) = E_{(s,a,s') \sim D} \left[ \left( Q_\phi(s,a) - (r(s,a) + \gamma E_{a' \sim \pi_\theta(a'|s')} [Q_\phi(s', a')] ) \right)^2 \right]$$

注意公式中的目标值（Target Value）部分：$r + \gamma E_{a' \sim \pi_\theta}[Q(s', a')]$。

• 为了计算这个目标值，我们需要用当前正在学习的策略 $\pi_\theta$ 去采样下一个动作 $a'$。
• 然后把这个 $a'$ 喂给 Q 网络去估值。

依然存在的 OOD 风险

• 如果当前的策略 $\pi_\theta$ 还没有训练得很好（或者在某些状态下稍微偏离了数据分布），它产生的动作 $a'$ 就可能是分布外（OOD）的 。
• 一旦 $a'$ 是 OOD 的，Q 网络 $Q(s', a')$ 的输出就可能是错误的（通常是过高估计）。
• 这个错误的 Q 值会被作为目标值（Target），反向传播去更新 Q 网络，导致误差累积。

那么有什么方法让他不要产生OOD的动作吗

IQL#

这个方法的目的就是，逼近“数据集里表现最好的动作”：在不产生幻觉的前提下，尽可能贪婪（Greedy）。

在标准的 Q-Learning (比如 DQN 或 SAC) 中，更新 Q 值时使用 Bellman Optimality Equation：

$$Q(s, a) \leftarrow r + \gamma \max_{a'} Q(s', a')$$

请注意这个 $\max_{a'}$ 操作。为了找到最大值，算法通常会做两件事之一：

1. 对于离散动作：把所有可能的动作都输入 Q 网络，选最大的。
2. 对于连续动作（由 Actor-Critic 完成）：让当前的策略网络（Actor）生成一个它认为最好的动作 $a'$，然后输入 Q 网络评估。

• 在离线设置中，我们不能与环境交互。
• 策略网络（Actor）可能会为了追求高分，生成一个从未在数据集里出现过的奇怪动作（OOD 动作）。
• Q 网络（Critic）只见过数据集里的动作。对于这个未见过的 OOD 动作，Q 网络无法正确评估，往往会因为泛化误差给出一个虚高的估值（Overestimation）。
• 结果：算法以为发现了一个好的操作，于是拼命往这个 OOD 动作的方向更新，导致训练崩溃。

我们不再让 Actor 生成一个 $a'$ 然后去查 $Q(s', a')$，而是直接训练一个 $V(s)$ 函数。

• 目标：让 $V(s)$ 逼近 $\max_{a \in \text{dataset}} Q(s, a)$。
• 手段：Expectile Regression（那个非对称的 Loss）

1. 只看数据： 训练 $V(s)$ 的 Loss 函数里：

$$\ell(V(s), Q(s, a))$$

这里的 $(s, a)$ 严格来自离线数据集。我们完全没有让 Policy 去生成新动作，也没有去查询任何未知的 $a'$。 2. 隐式最大化（Implicit Maximization）： 虽然我们只用了数据集里的样本，但通过调节 Expectile 的参数 $\tau$（比如设为 0.9）： - 如果 $Q(s, a)$ 比 $V(s)$ 小，Loss 权重很小（忽略差的动作）。 - 如果 $Q(s, a)$ 比 $V(s)$ 大，Loss 权重很大（强迫 $V$ 往大的 Q 值靠拢）。 - 效果：$V(s)$ 会自动过滤掉那些平庸的动作，收敛到数据集分布的上边缘（即数据集中表现最好的那个 Q 值）。

CQL#

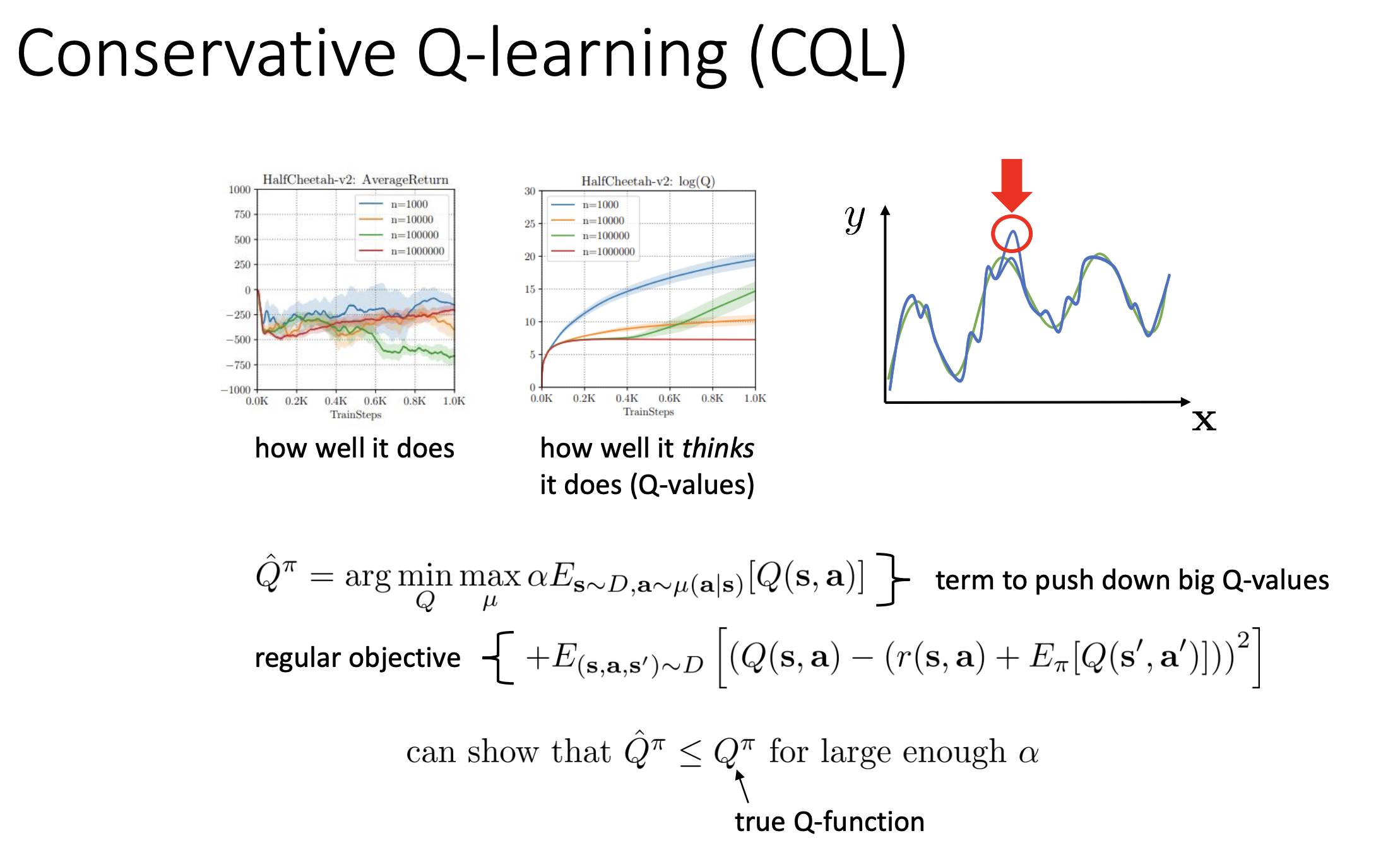这是另一种思路，我们说遇到OOD的时候我们会可能会错误估计这个动作的Q value，于是乎我们的思路就是打压这种错误估计的分数

$$+ E_{(\mathbf{s}, \mathbf{a}, \mathbf{s'}) \sim D} [(Q(\mathbf{s}, \mathbf{a}) - \text{target})^2]$$

• 这是标准的强化学习（Q-learning）目标。
• 它的意思： “即使我在做离线学习，我也要尽量让预测的 Q 值准确，能够反映真实的奖励。”

“压低”陌生动作的分数（Push Down）

$$\alpha E_{\mathbf{s} \sim D, \mathbf{a} \sim \mu(\mathbf{a}|\mathbf{s})}[Q(\mathbf{s}, \mathbf{a})]$$

• $\mathbf{a} \sim \mu$ 是什么意思？ 这里的 $\mu$ 通常代表模型当前认为“可能很高分”的动作，或者是随机采样的动作。重点是，这些动作不是直接从数据集里拿出来的，而是模型自己“脑补”出来的。
• 为什么要压低（Min）它？ 在离线强化学习中，最大的坑就是**“不懂装懂”。模型没见过某个动作，却错误地以为这个动作能得 10000 分（这就是 OOD 高估问题）。 所以这一项说：“凡是你（模型）自己想出来的、数据集中没见过的动作，我都先假设它是坏的，强行把它的 Q 值压低。”**

“抬高”已知数据的分数（Push Up）

$$-\alpha E_{(\mathbf{s}, \mathbf{a}) \sim D}[Q(\mathbf{s}, \mathbf{a})]$$

• 注意前面的负号： 整个大目标是最小化（Min），所以“减去”一项，等于是在最大化这一项。
  • $\mathbf{a} \sim D$ 是什么意思？ 这些是真真切切存在于数据集里的动作。
• 为什么要抬高它？ 这一项说：“但是，如果这个动作是数据集里有的，那就是有事实依据的，我要把它保护起来，把它的分数推高。” 最终结果： 只有数据集覆盖的地方（Data Region），Q 值是凸出来的（高的）；而在没有数据的地方（OOD Region），Q 值都被压得低低的。 这样一来，当你用这个 Q 函数去选动作时，它会自动倾向于选择那些高的区域（也就是数据集里的动作），从而避免去选那些未知的、可能有坑的区域。这就是所谓的**“Conservative（保守）”。

Model base offline RL#

MOPO#

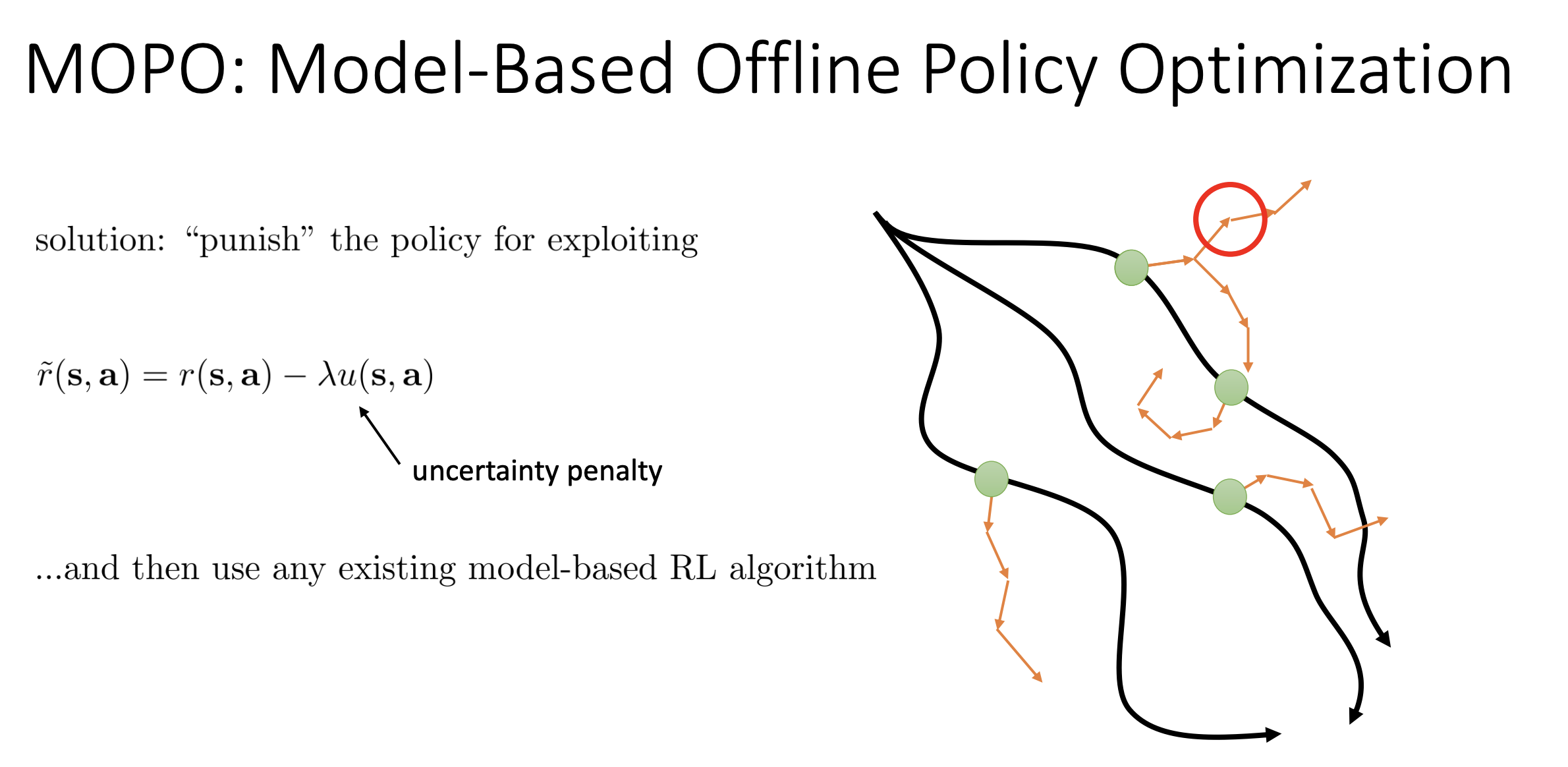这张 PPT 介绍的是一种名为 MOPO (Model-Based Offline Policy Optimization) 的强化学习算法。它的核心思想是如何在“离线强化学习”（Offline RL）中，利用基于模型（Model-Based）的方法来安全地优化策略。

• Offline RL（离线强化学习）： 智能体不能与环境交互，只能从一个固定的历史数据集（Dataset）中学习。
• 问题（Exploiting）： 如果智能体构建了一个环境模型（Model），并在该模型中进行规划，它往往会发现一些模型预测不准确但看起来奖励很高的区域（模型误差）。智能体容易“利用”这些误差，导致在真实环境中表现很差。这被称为 Distribution Shift（分布偏移） 问题。

PPT 左侧提出了核心解决方案：“Punish the policy for exploiting”（惩罚策略的利用行为）。

• 核心公式：

$$\tilde{r}(\mathbf{s}, \mathbf{a}) = r(\mathbf{s}, \mathbf{a}) - \lambda u(\mathbf{s}, \mathbf{a})$$

• $\tilde{r}(\mathbf{s}, \mathbf{a})$：修改后的奖励函数。

• $r(\mathbf{s}, \mathbf{a})$：原始的奖励函数。

• $u(\mathbf{s}, \mathbf{a})$：不确定性（Uncertainty）。这代表模型对自己预测的置信度。如果当前状态和动作偏离了训练数据（即模型没见过），不确定性 $u$ 就会很大。

• $\lambda$：惩罚系数。

• 直观理解： 算法通过人为降低那些“模型不确定区域”的奖励值，迫使智能体待在模型确信的区域（也就是接近真实数据分布的区域），从而避免由于模型误差导致的策略失效。

• 红色圆圈： 代表模型推演进入了未知区域（High Uncertainty）。在这种地方，MOPO 算法会通过上述公式给予高额惩罚，告诉智能体“这里很危险，不要往这里走”。

COMBO#

MOPO是通过“修改奖励”来避开风险，那么COMBO则是通过压低 Q 值来通过风险。

• 借鉴 CQL： PPT 开头提到“just like CQL…”。它的核心是：对于未见过的数据，直接把它们的 Q 值（预期回报）压得很低，以此来保持“保守”。
• COMBO 的做法： 它将 CQL 的思想应用到了 Model-Based 方法中。它不需要像 MOPO 那样去计算复杂的“不确定性惩罚”，而是简单粗暴地：凡是模型生成的（可能是假的）数据，我就在训练 Q 函数时，刻意去最小化它们的 Q 值。

COMBO 的核心目标函数，可以拆解为两部分看：

$$\hat{Q}^{k+1} \leftarrow \arg \min_Q \beta (\underbrace{\mathbb{E}_{s,a \sim \rho(s,a)}[Q(s,a)]}_{\text{压低模型数据的 Q 值}} - \underbrace{\mathbb{E}_{s,a \sim \mathcal{D}}[Q(s,a)]}_{\text{抬高真实数据的 Q 值}}) + \underbrace{\frac{1}{2}\dots}_{\text{标准 Q 学习}}$$

• 第一部分（保守项）： $\beta (\dots)$
  • 最小化模型生成数据 ($\rho(s,a)$) 的 Q 值：因为模型推演的数据可能是错误的（幻觉），为了安全，算法假设这些路径是“坏”的。
  • 最大化真实数据 ($\mathcal{D}$) 的 Q 值：因为真实数据是 Ground Truth，是可以信任的。
  • 通过这一减一加，人为地拉开了“真实数据”和“模型伪造数据”之间的价值差距。
• 第二部分（标准项）：
  • 这就是标准的 Bellman Error（TD Error），用于让 Q 函数学习正常的预测任务。

如果模型生成了一些“离谱”的数据（即看起来和真实数据完全不一样，属于 Out-of-Distribution），通过上面的公式，Q 函数会很容易把这些离谱数据的价值（Q值）打得很低。这样一来，策略（Policy）在做决策时，自然就不会去选择那些动作，从而避免了模型误差带来的风险。