CS285 Lecture2 Imitation Learning • Laurie's Site

行为克隆#

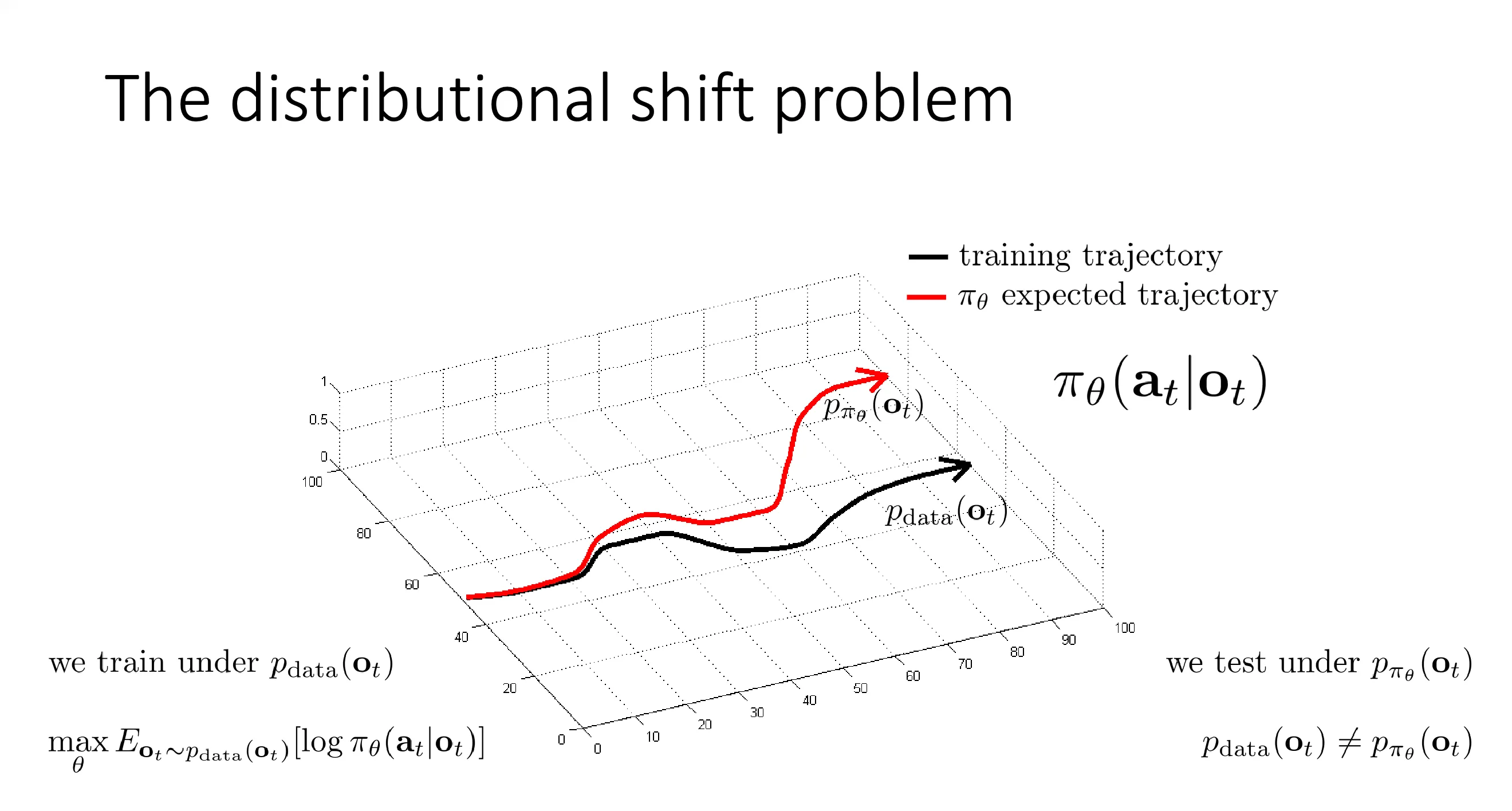
alt text

假设我们一开始有一个专家，他每次行驶同一个路线，重复很多遍。每一次他都有可能有不同的操作，比如在相同的时刻t，前一次和后一次在的位置不一样，他的操作也不一样，但是最终都能顺利行驶完这个路线。于是乎，我们就有了一个数据集，

1：(o_{t-1}, a_{t-1}), (o_t, a_t), (o_{t+1}, a_{t+1})

2：(o_{t-1}, a_{t-1}), (o_t, a_t), (o_{t+1}, a_{t+1})

3：(o_{t-1}, a_{t-1}), (o_t, a_t), (o_{t+1}, a_{t+1})

...

前面的1，2，3表示第几次行驶这个路线，然后括号内的一对表示当前时刻 t 观察到场景 $o_t$ 之后采取的动作 $a_t$ 。

由于每次时间t，你观察到的 $o_t$ 不一定一样，所以这里就有一个概率分布，可能50次是这种，另外20次是那种。图中的 $P_{data}(o_t)$ 表示的就是t时刻观察场景o的概率分布。

$\pi_\theta(a_t|o_t)$ 表示的就是策略 $\pi_\theta$ 在给定 $o_t$ 的情况下输出 $a_t$ 的概率。 $P_{\pi_\theta}(o_t)$ 表示的就是我采用策略 $\pi_\theta$ 的情况下我的概率分布会是什么。

当然按理来说这两个概率分布P都应该是一条点状云，图中从中抽样出一次的数据就用线来表示了，只是方便演示。

行为克隆就是将训练当成一个有监督训练，目标就是最大化给定专家数据中的输入 $o_t$ ，输出对应的动作 $a_t$ 的概率最大。

\max_{\theta} \mathbb{E}_{\mathbf{o}_t \sim p_{\text{data}}(\mathbf{o}_t)} [\log \pi_{\theta}(\mathbf{a}_t | \mathbf{o}_t)]

我们从数据集中随机抽一些数据可能是第4次的时间步5，第6次的时间步3等等，将他们抽出来让模型去预测，让他预测到对应动作的概率最大。

于是这里就有一个问题，在有监督中，我们的先验假设就是数据点之间是独立同分布的，但是很显然这里不可能，这里就是一个隐患，模型学到的很可能就是单帧的预测，而不是连续的依赖。

以及如果出现了以前没有见过的数据，那很可能模型的表现就会很不好，而且这种错误会不断累加。

问题就是我们的训练数据都是在 $P_{data}$ 中抽取的，而我们实际在乎的是在测试中的表现，然后由于行为克隆是本身上一次的决策会影响下一次的决策，这里面的错误可能不断累加，导致他最终的分布会不断的偏离原本的专家分布，这就叫做分布偏移。

于是乎我们抛弃原本的思路，换一种思路

c(\mathbf{s}_t, \mathbf{a}_t) = \begin{cases} 0 & \text{if } \mathbf{a}_t = \pi^{\ast}(\mathbf{s}_t) \\ 1 & \text{otherwise} \end{cases}

$\pi^{\ast}(\mathbf{s}_t)$ 为专家在这种情况下做的动作，如果我们的策略预测的动作和专家的一样，那我们就不会有惩罚，否则就惩罚。然后我们的优化目标就变成

\text{minimize} \quad \mathbb{E}_{\mathbf{s}_t \sim p_{\pi_{\theta}}(\mathbf{s}_t)} [c(\mathbf{s}_t, \mathbf{a}_t)]

注意这种情况下，我们的分布是在 $p_{\pi_\theta}$ 下面.

Some analysis#

alt text

假设我们用自监督有一个很好的模型，在训练数据集中他的预测结果很精确。

\text{assume: } \pi_{\theta}(\mathbf{a} \ne \pi^{\ast}(\mathbf{s})|\mathbf{s}) \le \epsilon \; (\text{for all } \mathbf{s} \in \mathcal{D}_{\text{train}})

他的预测概率失败概率小于 $\epsilon$

假设我的总时长为T，我们可以计算出他的平均惩罚的上界是多少。右边的公式就是假设我从一开始就预测错误，然后之后的动作全都跟着预测错误，然后第一步错的概率是 $\epsilon$ ，然后后面跟着全错他的惩罚就是T，所以第一部分的期望就是 $\epsilon T$ ，然后以此类推。第二项就是第一步没错的情况下概率是 $1-\epsilon$ ,然后第二步开始错了 $\epsilon(T-1)$ 一直往后。

\underbrace{E\left[\sum_tc(\mathbf{s}_t,\mathbf{a}_t)\right]}_{O(\epsilon T^2)}\leq\underbrace{\epsilon T+(1-\epsilon)(\epsilon(T-1)+(1-\epsilon)(\ldots))}_{T\text{ terms, each }O(\epsilon T)}

所以说可以看到他最坏情况下复杂度是 $O(\epsilon T^2)$ ,这显然不是一个很好的结果，我们可以接受的应该是线性的，高于线性的可能就不是这么好。

more analysis#

上面的分析我们要求的条件太严格了，我们要求训练集中的所有数据他的出错率都要小于 $\epsilon$ ，于是乎我们放宽一点，更general一点。

我们假设我们从 $P_{train}(s)$ 分布里面抽一些出来s，然后假设他的平均出错小于 $\epsilon$ ，这种情况下更符合现实。

E_{p_{\mathrm{train}}(\mathbf{s})}[\pi_\theta(\mathbf{a}\neq\pi^\star(\mathbf{s})|\mathbf{s})]\leq\epsilon

于是乎我们可以进行如下推导

\begin{aligned} & p_\theta(\mathbf{s}_t)=(1-\epsilon)^t{ \begin{array} {c} \end{array}}p_{\mathrm{train}}(\mathbf{s}_t)+(1-(1-\epsilon)^t){p_{\mathrm{mistake}}(\mathbf{s}_t)}_{ \begin{array} {c} \end{array}} \end{aligned}

我们可以先将他的概率分布分成两部分，第一部分就是前t步都符合 $P_{train}$ 概率分布他的概率就是 $(1-\epsilon)^t$ 之后就是不符合的部分。 $P_{mistake}$ 是个很复杂的分布，我们不知道他是什么。

之后左右两边减去一个 $P_{train}$ 可以化简一下，这里的2感觉有点奇怪，可能是为了进一步放缩一下。

|p_\theta(\mathbf{s}_t)-p_{\mathrm{train}}(\mathbf{s}_t)|=(1-(1-\epsilon)^t)|p_{\mathrm{mistake}}(\mathbf{s}_t)-p_{\mathrm{train}}(\mathbf{s}_t)|\leq2(1-(1-\epsilon)^t)

之后根据伯努力不等式再放缩一下， $\text{useful identity: }(1-\epsilon)^t\geq1-\epsilon t\mathrm{~for~}\epsilon\in[0,1]$ 右边部分就又 $\leq2\epsilon t$

之后进一步推导，我们想知道他的平均的惩罚是多少

\begin{aligned} \sum_tE_{p_\theta(\mathbf{s}_t)}[c_t]=\sum_t\sum_{\mathbf{s}_t}p_\theta(\mathbf{s}_t)c_t(\mathbf{s}_t) & \leq\sum_t\sum_{\mathbf{s}_t}(p_{\mathrm{train}}(\mathbf{s}_t)c_t(\mathbf{s}_t)+|p_\theta(\mathbf{s}_t)-p_{\mathrm{train}}(\mathbf{s}_t)|c_{\mathrm{max}}) \\ & \begin{aligned} \leq\sum_t(\epsilon+2\epsilon t)\leq\epsilon T+2\epsilon T^2 \end{aligned} \\ & O(\epsilon T^2) \end{aligned}

第一个小于号那里他将 $p_\theta$ 变成了 $p_{train}$ ，然后补上他们之间的差值，具体过程就是

\begin{aligned} p_\theta(\mathbf{s}_t)c_t(\mathbf{s}_t)&=p_{train}(\mathbf{s}_t)c_t(\mathbf{s}_t)+p_\theta(\mathbf{s}_t)c_t(\mathbf{s}_t)-p_{train}(\mathbf{s}_t)c_t(\mathbf{s}_t)\\ &=p_{train}(\mathbf{s}_t)c_t(\mathbf{s}_t)+|p_\theta(\mathbf{s}_t)-p_{\mathrm{train}}(\mathbf{s}_t)|c_t(s_t)\\ &\le p_{train}(\mathbf{s}_t)c_t(\mathbf{s}_t)+|p_\theta(\mathbf{s}_t)-p_{\mathrm{train}}(\mathbf{s}_t)|c_{max} \end{aligned}

然后前面那一部分就是我们一开始的假设就 $\le \epsilon$ ,后面那一部分就是之前推导出来的 $\leq2\epsilon t$ 进一步计算我们也可以得到他的上界复杂度也是 $O(\epsilon T^2)$ 。

Paradox#

先前我们将行为克隆比做走钢丝的人，一旦有一步走错，你就没有恢复的可能。这是因为标准的行为克隆，它的训练数据 $D_train$ 全是专家完美驾驶的黑色轨迹，数据里根本没有任何关于“如何从错误中恢复”的信息。你不可能学会你从未见过的东西。于是乎这里就有一个悖论：如果数据包含更多的错误（和恢复），模仿学习的效果可能会更好。

不止是包含更多错误及恢复，数据增强也是可以的，比如训练一个无人机穿过森林的时候，人可以走一遍路线，然后佩戴一个左中右三个摄像头的头盔，然后左边摄像头采集的数据标注就是右转，右边的摄像头采集的数据标注就是左转，中间的就标注直走，用这些数据来训练无人机

Why might we fail to fit the expert?#

为什么对于简单的行为克隆，基于当前的图像输入，然后获得输出他也不是很能很好的拟合专家呢，可以从两个方面入手

Non-Markovian behavior#

人类的行为很多时候都不是一个马尔可夫的决策过程，当做出决策的时候人们不会只根据当前的状态来做出反应，而是强烈依赖历史（例如刚刚看到盲区有车、刚被人加塞情绪受影响等），因此同一画面在不同上下文下可能做出不同行为

解决这种问题可能就是用CNN之类的编码图像然后把编码出的向量输入进一个序列模型（LSTM、Transformer、时序卷积等）把一段历史观测编码进策略，让策略根据整段历史输出当前动作

但是这种方法也不总是好事，引入历史信息有时会引发“因果混淆”，模型可能学到错误的相关性。设想用行为克隆训练自动驾驶：

专家是“看到前方障碍/红灯 → 踩刹车 → 仪表盘上刹车灯亮”。真正的因果关系是“前方情况导致踩刹车，踩刹车导致灯亮”。
如果把“历史信息”也喂给模型，比如上一时刻“刹车灯是否亮”，模型发现：数据里只要灯亮，专家几乎总是刹车，于是学成了“看到灯亮就继续踩刹车”，把“刹车灯”（刹车的结果）当成“踩刹车的原因”。

Multimodal behavior#

当我们使用L2回归( $L=∥a_{expert}−\hat{a}(s)∥^2$ )来训练模型的时候，他就会假设 $a_{expert}$ 的分布就是一个单峰的正态分布，这是为什么呢？

首先假设我们的回归模型如下：

y_i = f_\theta(x_i) + \epsilon_i, \quad i=1,\dots,n

其中：

$x_i$ ：第 $i$ 个样本输入
$y_i$ ：对应的真实输出
$f_\theta(x_i)$ ：模型对 $x_i$ 的预测（参数是 $\theta$ ，可以是线性模型、神经网络等）
$\epsilon_i$ ：噪声 / 误差

关键假设： 误差服从高斯分布，且相互独立、同分布 (i.i.d.)：

\epsilon_i \sim \mathcal{N}(0, \sigma^2)

因为 $\epsilon_i = y_i - f_\theta(x_i)$ ，所以给定 $x_i$ 和参数 $\theta$ 时， $y_i$ 的条件分布是：

y_i \mid x_i, \theta \sim \mathcal{N}\big(f_\theta(x_i), \sigma^2\big)

根据高斯分布的概率密度函数 (PDF)：

p(y_i \mid x_i, \theta) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - f_\theta(x_i))^2}{2\sigma^2} \right)

这表示：预测值 $f_\theta(x_i)$ 越接近真实值 $y_i$ ，这个样本在当前模型参数下出现的概率（似然）就越大。

假设各个样本相互独立，那么总体的 似然函数 为所有样本概率的乘积：

L(\theta) = \prod_{i=1}^{n} p(y_i \mid x_i, \theta) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y_i - f_\theta(x_i))^2}{2\sigma^2} \right)

我们的目标是做 最大似然估计 (MLE)，即找到一组参数 $\theta$ ，使得观测到当前数据的概率最大：

\theta^* = \arg\max_\theta L(\theta)

由于对数函数 $\log$ 是单调递增的，最大化 $L(\theta)$ 等价于最大化 $\log L(\theta)$ （对数似然）：

\log L(\theta) = \sum_{i=1}^{n} \left[ \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{(y_i - f_\theta(x_i))^2}{2\sigma^2} \right]

我们将常数项和与 $\theta$ 无关的部分分离出来：

第一项 $\log \frac{1}{\sqrt{2\pi\sigma^2}}$ 是常数，不依赖于 $\theta$ 。
唯一包含 $\theta$ 的是第二项（平方误差项）。

简化后可写为：

\log L(\theta) = C - \frac{1}{2\sigma^2} \sum_{i=1}^{n} (y_i - f_\theta(x_i))^2

(其中 $C$ 是与 $\theta$ 无关的常数)

我们要最大化对数似然：

\theta^* = \arg\max_\theta \left[ C - \frac{1}{2\sigma^2} \sum_{i=1}^{n} (y_i - f_\theta(x_i))^2 \right]

注意公式中的负号。要让整个式子最大，必须让减去的后面那部分最小。同时，系数 $\frac{1}{2\sigma^2}$ 是正数，不影响极值点的位置。

因此，问题等价于：

\theta^* = \arg\min_\theta \sum_{i=1}^{n} (y_i - f_\theta(x_i))^2

这就是标准的 最小二乘 (L2) 损失：

\boxed{ \mathcal{L}_{L2}(\theta) = \sum_{i=1}^{n} (y_i - f_\theta(x_i))^2 }

假设误差服从高斯分布，使用最大似然估计 (MLE) 求得的最优参数，在数学上等价于最小化误差的平方和 (L2 Loss)。

所以说当我们使用L2回归的时候就是假设我们的 $a_{expert}$ 是一个单峰的正态分布，所以训练的目标就是不管数据的分布如何，单峰还是多峰，我都用一个单峰的正态分布根据最大似然去近似，输出其实就是这个正态分布的均值，目标就是让模型输出的这个均值所对应的正态分布能尽可能的拟合真实分布。

但是，如果实际 $a_{expert}$ 是多峰的，假设有左右两个峰，那么我们的模型就是输出左右两个峰的中间值，这样他对应的正态分布可以最可能的贴合这个多峰的分布。这就有一个问题，可能左右峰对应的值是合理的，但是中间的输出值就是不合理的。就比如滑雪时中间有一颗树，我要绕过这个树，从左绕和从右绕都可以，面对同一个场景有两种动作，这些都在数据集里面，那么他的数据分布就是两个峰，如果这时候模型输出中间值，那就是不合理的。

既然这样，怎么解决呢？

可以不用单峰的高斯分布，输出均值这种，换一个分布
可以用离散的输出，这个输出可以表示高维度

Expressive continuous distributions#

mixture of gaussians（混合高斯）#

第一种就是用混合高斯模型来表示 $a_{expert}$ 的分布, 用多元高斯的最大似然来当作损失函数

\mathcal{L} = -\log \sum_{k=1}^{K} w_k(\boldsymbol{s}) \mathcal{N}(\boldsymbol{a}_{\text{expert}} | \boldsymbol{\mu}_k(\boldsymbol{s}), \boldsymbol{\Sigma}_k(\boldsymbol{s}))

模型的输出就是

项目	维度	含义
$\mu_k(s)$	K × action_dim	每个模式的均值
$\Sigma_k(s)$	K × action_dim (或对角矩阵)	每个模式的方差
$w_k(s)$	K 个	每个模式的混合权重（sum=1）
但是他的问题就是你的K是一个超参数，如果你的模态很多比如机器人可以上千种，那就很难训练了

latent variable models(潜变量模型)#

简单来说就是

          z (隐藏策略)
          ↓
s (状态) → policy → a (动作)

scss

1. 以 CVAE + BC 为例（训练阶段）

在训练时，模型主要做两件事：

① 编码器（Recognition Model）：学习 $z$

q_\phi(z \mid s, a)

含义： 看到专家在状态 $s$ 采取了动作 $a$ ，逆向推断这个动作属于哪种“隐藏策略” $z$ 。
示例：
- 左绕树 $\rightarrow$ 编码器可能输出 $z \approx (-1, 0.2)$
- 右绕树 $\rightarrow$ 编码器可能输出 $z \approx (1.1, -0.3)$
- $z$ 把动作背后的“模式”编码了出来。

② 解码器（Policy）：学习从 $z$ 生成动作

p_\theta(a \mid s, z)

含义： 给定状态 $s$ 和隐藏策略 $z$ ，生成专家会采取的动作 $a$ 。
示例：
- 输入 $s$ （树在前面）+ $z$ （左绕） $\rightarrow$ 输出负方向动作
- 输入 $s$ （树在前面）+ $z$ （右绕） $\rightarrow$ 输出正方向动作

③ 训练目标 我们在训练中最大化 Evidence Lower Bound（ELBO）：

\mathcal{L} = \mathbb{E}_{q_\phi(z|s,a)}[\log p_\theta(a|s,z)] - \text{KL}(\dots)

这背后的机制是：模型强制让 $z$ 存储“多模态结构”，让 $p(a|s,z)$ 存储“特定模式下的动作生成”。

2. 推理（Test）阶段： $z$ 变成“策略选择器” 这一步最关键。推理时没有专家动作 $a$ ，所以不能使用编码器，操作如下： ① 从先验分布采样

z \sim p(z) = \mathcal{N}(0, I)

② 生成动作

a = p_\theta(a \mid s, z)

③ 多模态策略的体现

如果采样多个不同的 $z$ ，会得到多个不同的动作：

采样 $z_1 \rightarrow$ 左绕动作
采样 $z_2 \rightarrow$ 右绕动作
采样 $z_3 \rightarrow$ 速度慢一点
采样 $z_4 \rightarrow$ 速度快一点

这就是引入潜变量 $z$ 解决多模态问题的根本原因。

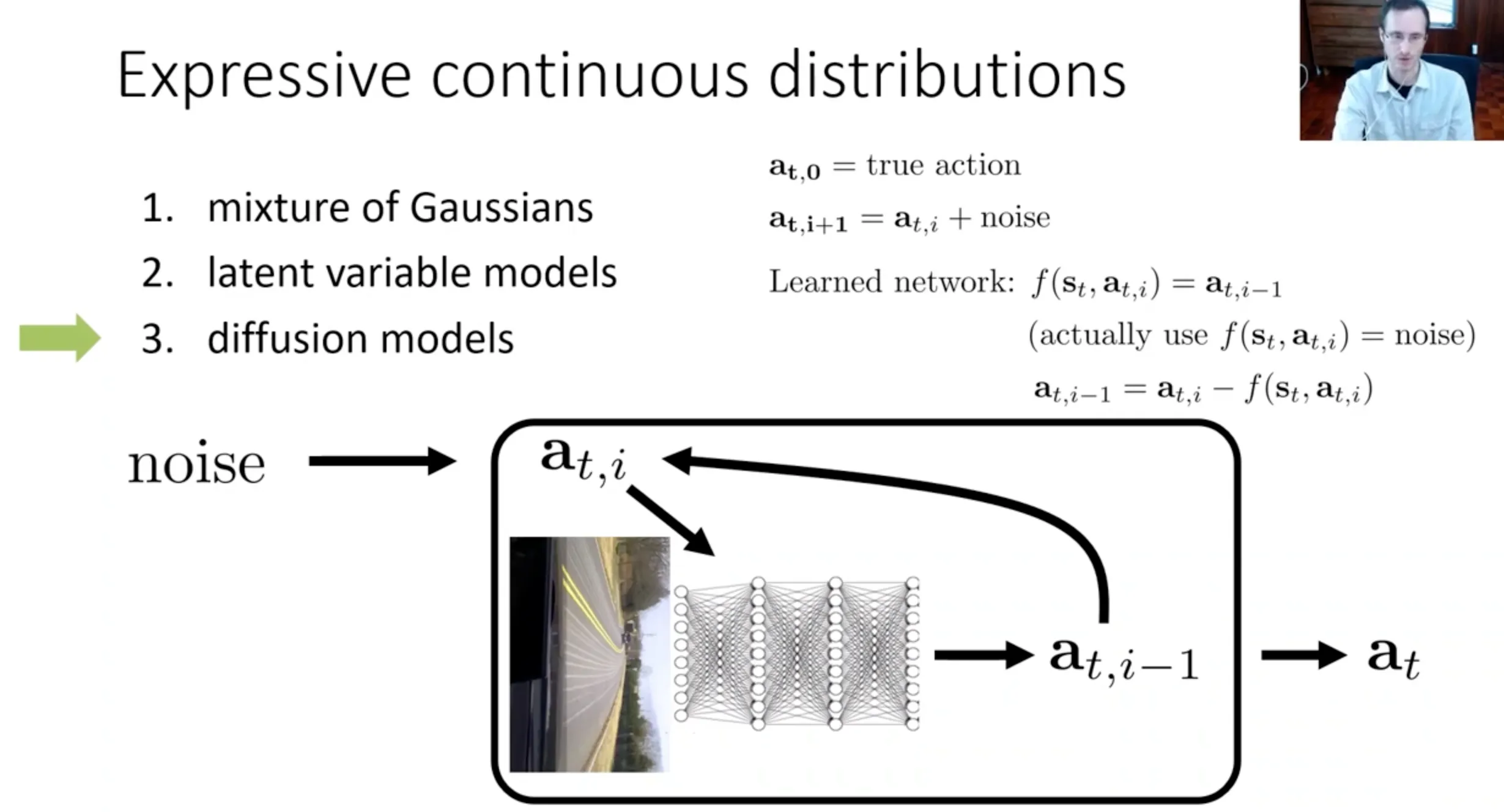
diffusion models（扩散模型）#

不断去噪最终生成动作 alt text

multi-task learning#

主要讲了一种让行为克隆更“抗错”的思路：用多任务/多目标的“目标条件行为克隆”（goal‑conditioned behavioral cloning，GCB）和回顾重标（hindsight relabeling）

核心想法#

传统行为克隆只学“从起点到固定目标 P1 的最佳轨迹”，数据覆盖的状态分布很窄，因此一旦策略犯错偏离演示轨迹，就会落到没见过的状态，误差会不断放大（分布偏移）。
讲者提出：与其费劲让专家“故意犯错、再恢复”，不如收集专家去很多不同目标位置的演示，然后训练一个“输入当前状态 s 和期望目标状态 g（如轨迹最后一帧）→ 输出动作 a”的目标条件策略，这样可以显著增加覆盖的状态空间并利用更多次优数据。

目标条件行为克隆与回顾重标#

数据收集：拿到很多轨迹 demo，每条只是状态–动作序列，并不显式告诉“任务是什么”。假设“这条轨迹对到达它最后到达的状态 $s_T$ 是一个好示范”。
训练方式：对每条 demo，把最后一个状态 sTs_TsT 当作“目标 g”，把“当前状态 s、目标 g”喂给策略，监督它输出专家动作 a，相当于最大化 $\log \pi_\theta(a \mid s, g)$ 。
这相当于用“后见之明”（hindsight）：不管专家当时本来想干什么，都当作是在“成功到达最后状态 g 的演示”，因此可以从大量“玩耍式”数据中提取出覆盖很广的目标到达能力。

多任务带来的好处和理论问题#

好处：
- 由于有很多不同目标，专家会访问更多多样的状态，因此策略更难遇到完全没见过的状态；即使用于特定目标 P1 时，也能在错误状态附近找到“类似于其他目标演示中的状态”，学会自我纠正。
- 可以充分利用次优数据：即使专家没成功到 P1，只要成功到达某个别的位置，也能作为“到达那个位置”的正例。
理论上的隐患：这种方法在理论上产生了“两处分布偏移”（一个是策略状态分布 vs. 数据状态分布，另一个是由这种“后见之明标注目标”的方式引入的偏移）

DAgger#

分布偏移的本质是：训练时的数据分布 pdatapdata 和测试时在当前策略下访问到的状态分布 $p_{π_θ}$ 系统性不同，小错误会把策略带到“没见过的状态”，然后错误不断放大。

可以看到，为了解决分布偏移的问题，也就是尽可能让 $p_{data}=p_{π_θ}$ ，之前的策略都是让策略更少犯错，让 $p_{π_θ}$ 去逼近 $p_{data}$ 。但是我们可以反过来，通过在线收集数据让训练数据分布逐渐变成策略实际访问到的分布，让 $p_{data}$ 去逼近。 alt text

第一步，用专家 demonstration 先训练一个初始策略，然后在真实环境中运行这个策略，记录它看到的所有 observation（状态）。
第二步，请专家对这些 observation 逐一打标签：如果是 TA 操作，会在每个状态下采取什么动作，由此得到一个“基于当前策略分布”的带标签数据集。
第三步，把这些新数据和原本示范数据 union 起来，重新训练策略，再次上线跑、再收集、再标注、再聚合，如此循环；可以证明数据中的状态分布会逐步逼近当前策略实际访问到的分布，理论上可以把错误界从随时间的二次增长降成线性增长，但代价是必须能不断获得这些额外专家标签。

但是有一个主要问题是“离线打标签”的不自然：人类开车或操控无人机时有反应时间和时序感，在事后看单帧图像标动作，和真实操作时的决策可能不一致，这使得 DAGGER 在一些任务上不太自然。