CS285 Lecture4 Introduction to Reinforcement Learning

Markov chain#

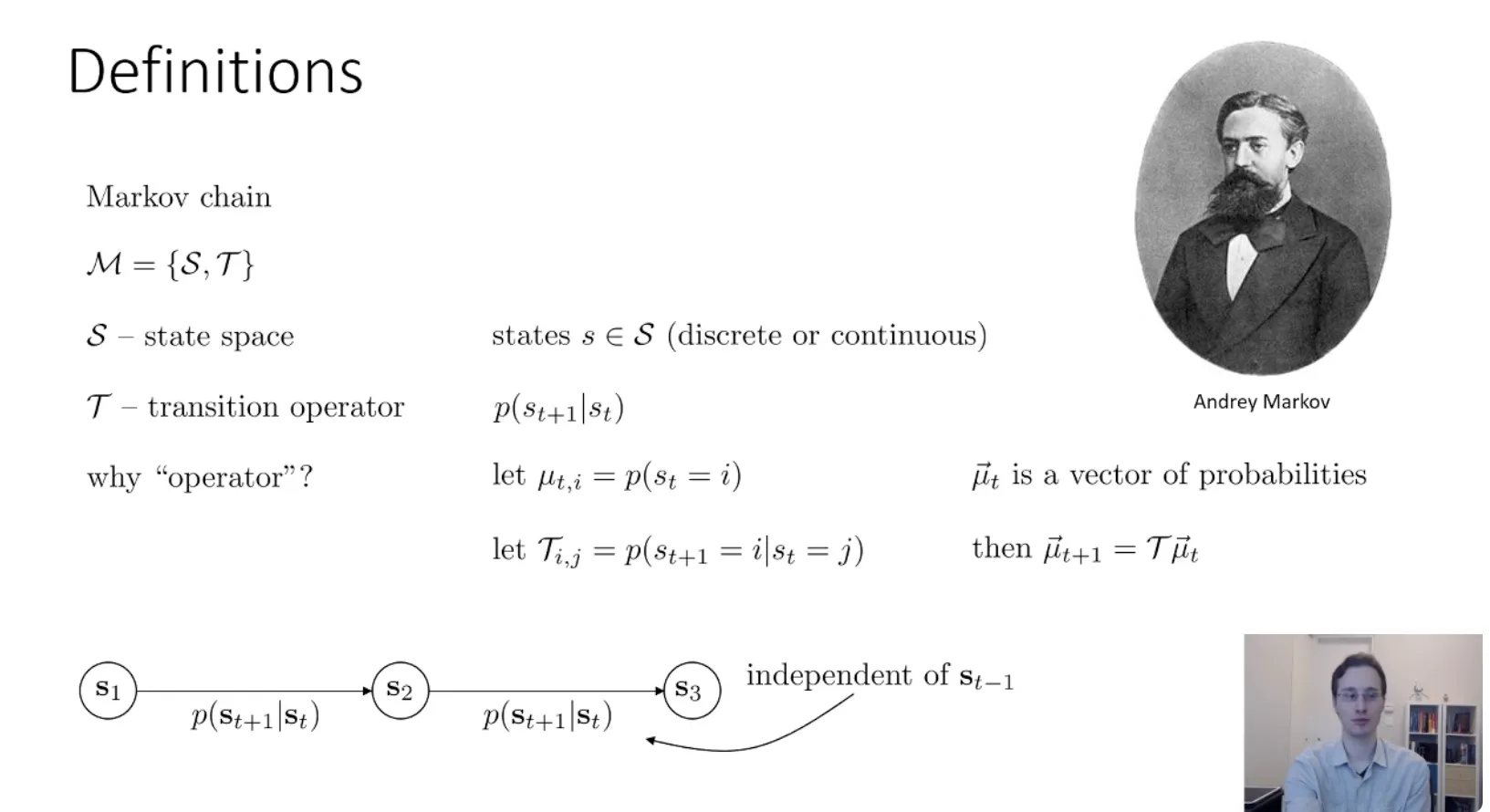
Markov decision process(马尔可夫决策过程)#

相比于马尔可夫链，他多的就是下一次的状态不止是和当前状态有关系，还和采取的动作有关系。以及多了一个奖励函数

Partially observed Markov decision process(部分观测马尔可夫决策过程)#

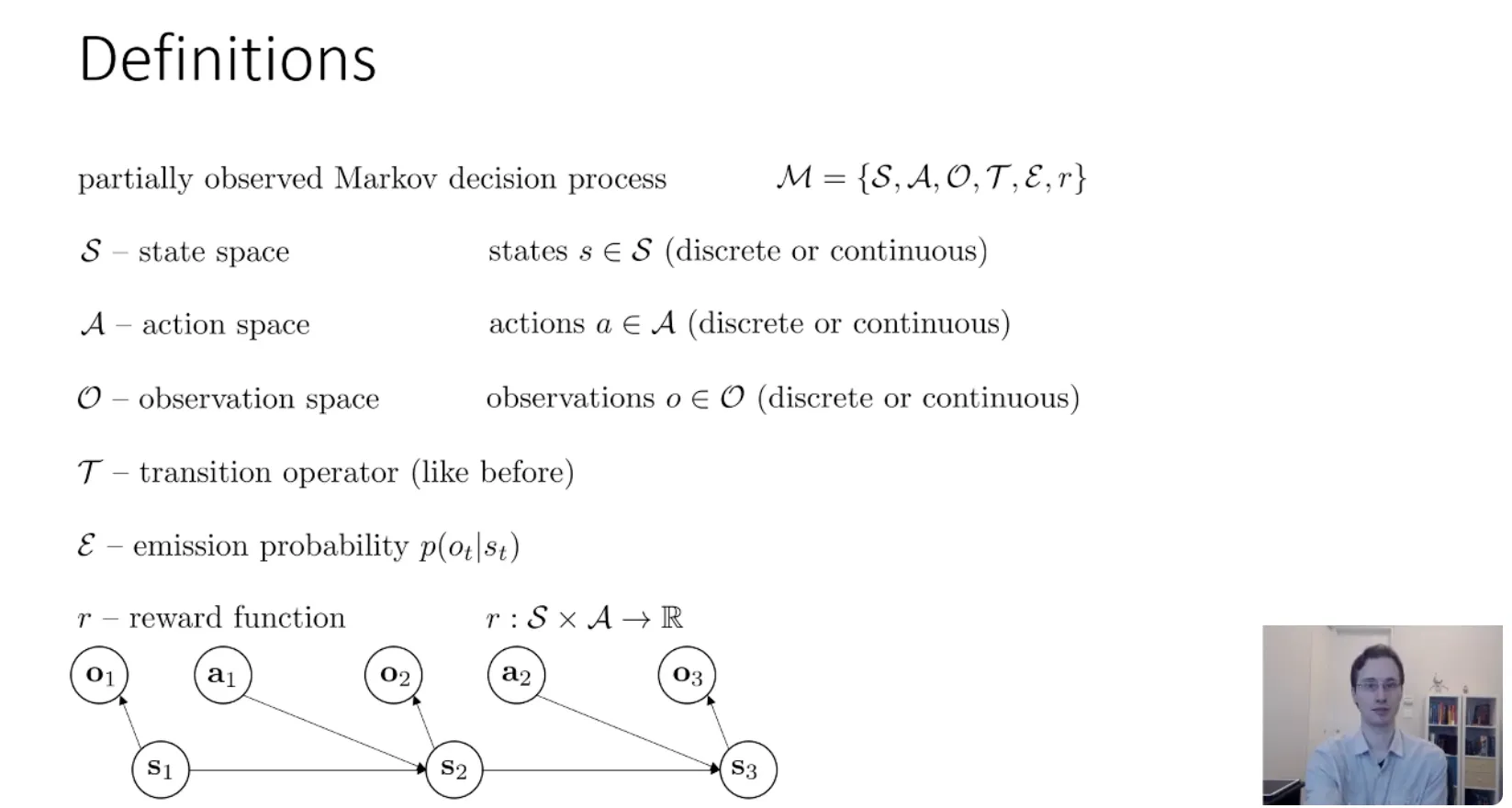$\mathcal{O}$ - Observation Space (观测空间)

• 定义：所有可能观测到的数据的集合。
• 比如：
  • $S$ (状态)：可能是杯子在绝对坐标系下的 (x, y, z) 坐标（这是上帝视角，你通常不知道）。
  • $O$ (观测)：是你的机器人摄像头拍到的像素图片，或者是雷达的扫描点云。
  • 机器人只能拿到 $o \in \mathcal{O}$，拿不到 $s$。

$\mathcal{E}$ - Emission Probability (发射概率)

• 定义：$p(o_t | s_t)$
• 含义：给定当前真实状态 $s_t$，观测到 $o_t$ 的概率是多少？
• 为什么叫“发射 (Emission)”？
  • 这是一个来自隐马尔可夫模型 (HMM) 的术语。你可以想象真实状态 $s$ 是隐藏在幕后的“发射源”，它向外“发射”出我们能看到的观测信号 $o$。
  • 例子：如果状态 $s$ 是“外面下雨了”，那么发射出的观测 $o$ 可能是“地面湿了”的概率是 90%，“有人打伞”的概率是 80%。

The goal of reinforcement learning#

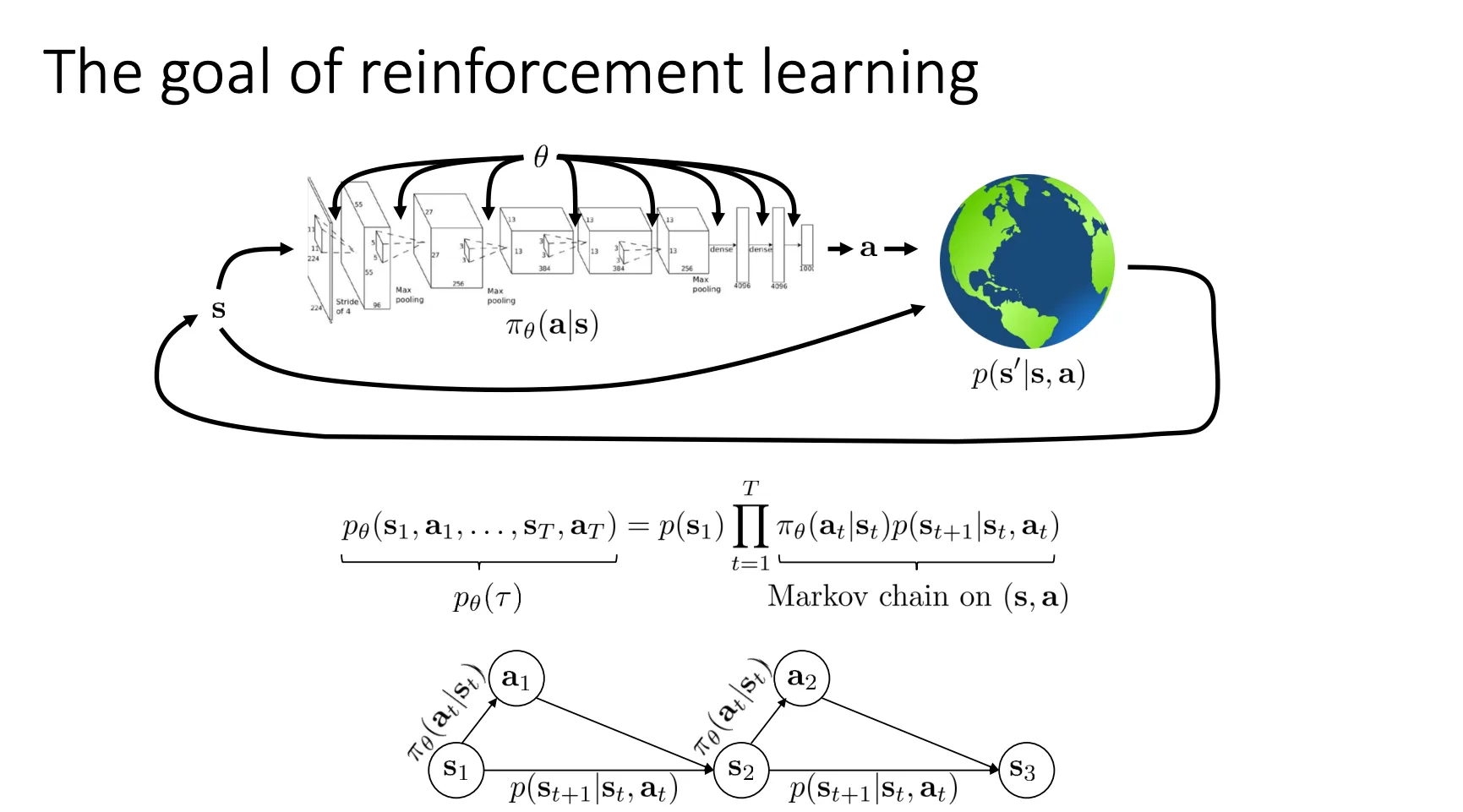这个ppt就用数学语言定义了强化学习的目标是什么

上面的公式就是 $\pi_\theta(\mathbf{a}_t|\mathbf{s}_t)$:面对当前画面 $\mathbf{s}_t$，智能体选择动作 $\mathbf{a}_t$ 的概率。 $p(\mathbf{s}_{t+1}|\mathbf{s}_t, \mathbf{a}_t)$: 当你做了动作 $\mathbf{a}_t$ 后，世界根据物理定律，演变到下一个状态 $\mathbf{s}_{t+1}$ 的概率。 然后从状态 $\mathbf{s}_{1}$ 开始，一连串事件要连续发生，所代表的轨迹发生的概率是多少

下面的那一个公式就是我们优化的参数目标 相同的参数我跑很多次，每次得到不同的轨迹和对应的概率，然后计算每个轨迹每一步的奖励，求和得到轨迹的总奖励，最终加权求和就是当前策略的奖励。我们的目标就是得到能使得这个奖励最大的策略。

我们还可以用另一种方式来表示，我们可以将这个过程看作是一个马尔可夫链而不是马尔可夫决策过程，把(s,a)看做一个状态，就变成

于是我们的优化就可以变成

$$\begin{align*} \theta^\star &= \arg \max_\theta E_{\tau \sim p_\theta(\tau)} \left[ \sum_t r(\mathbf{s}_t, \mathbf{a}_t) \right] \\ &= \arg \max_\theta \sum_{t=1}^T E_{(\mathbf{s}_t, \mathbf{a}_t) \sim p_\theta(\mathbf{s}_t, \mathbf{a}_t)} [r(\mathbf{s}_t, \mathbf{a}_t)] \end{align*}$$

这种转化的好处就是，当我的T是无穷的时候，他的奖励就不应该再是累加而应该是平均，因为趋于无穷，奖励和也趋于无穷就没有意义。

然后当我有一个马尔可夫链满足遍历性(Ergodic: 有机会从任何一个状态跳到任何另一个状态)，他的分布最终就会平稳。所以说面对平均，T趋于无穷，他就会趋于E里面的内容，所以我们只看这部分就可以了。

还有一点要提的就是，强化学习他的目标就是优化期望，即使我的奖励函数是离散的，但是他的期望是连续的，这就使得RL可以很好的进行优化

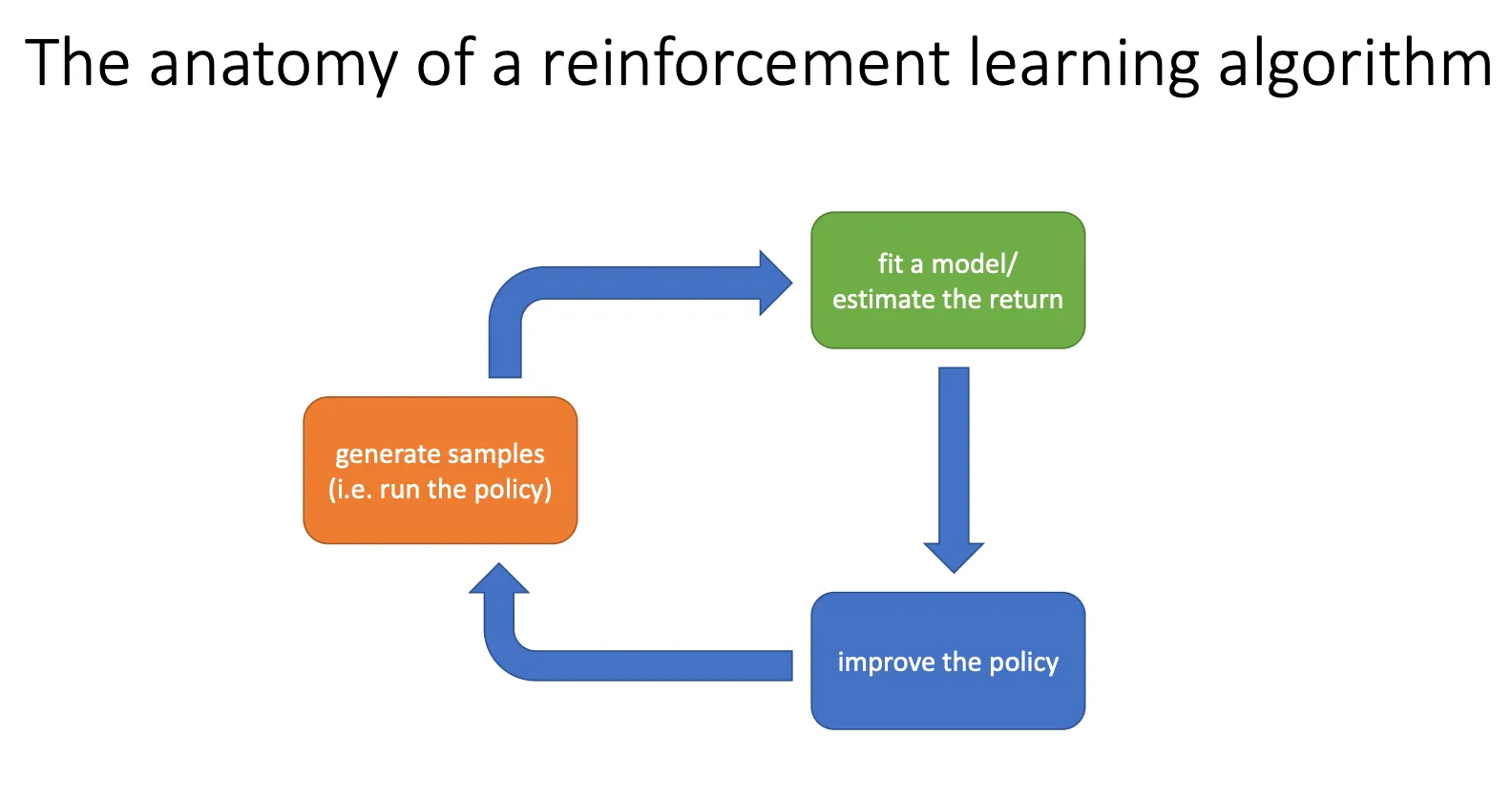
Algorithm#

我们可以将强化学习算法分为三个部分，采样，评估，训练 我们可以将之前的奖励拆分，定义Q function和value function，然后假设我们知道Q value，然后我们就可以根据这个来优化我们的模型

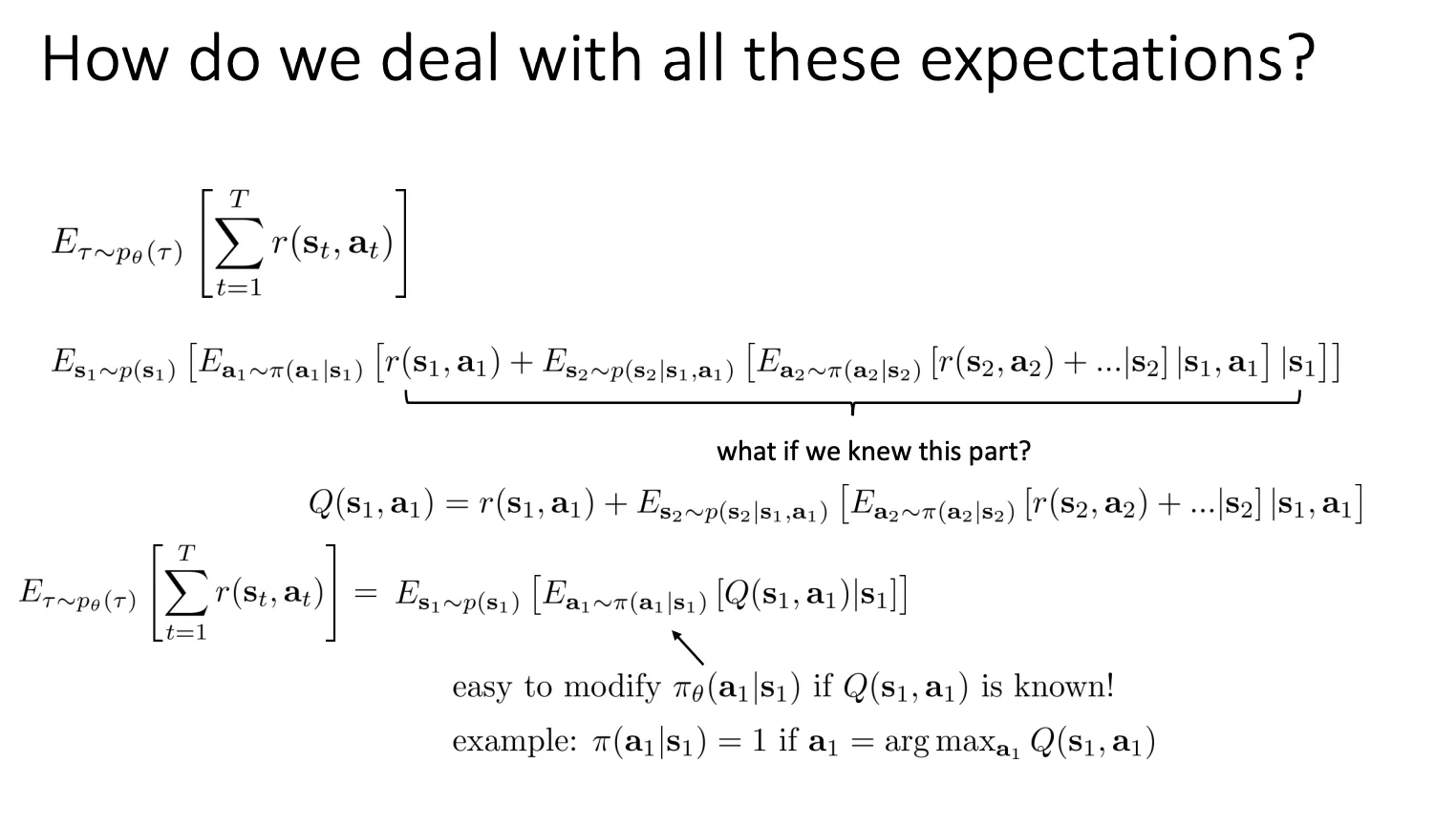
Tradeoffs Between Algorithms#

我们有很多种RL算法，每种算法都有自己的优缺点，所以我们需要权衡每一种算法

RL算法#

1. Policy Gradients (策略梯度法)#

• 核心思路：直接硬解。
• 怎么做： 我有一个神经网络（策略网络 $\pi_\theta$），它的输入是状态，输出是动作。我就盯着最终的得分看：
  • 如果这局分高，我就调整参数 $\theta$，让刚才做的动作出现概率变大。
  • 如果这局分低，我就调整参数 $\theta$，让刚才做的动作出现概率变小。
• 特点：
  • 它不直接去算 Q 值或 V 值（或者说不依赖它们的准确性），而是直接对目标函数求导（梯度上升）。
  • 比喻： 就像你在调收音机的旋钮。你不知道电路原理，但你听到声音清晰了就往那个方向多转一点，声音杂音大了就往回转。

2. Value-based (基于价值的方法)#

• 怎么做： 我根本不训练一个策略网络（No explicit policy）。我不去学“什么时候该跳”，而是去学“在这个状态下跳能得多少分”（即学习 $Q(s,a)$）。
  • 如果我们把完美的 $Q^*$ 函数学出来了，决策就超级简单：每次只选分最高的那个动作（Argmax）。
• 特点：
  • 典型的算法是 DQN（Deep Q-Network）。
  • 这里学的是**最优策略（Optimal Policy）**的价值。

3. Actor-Critic (演员-评论家算法)#

• 怎么做： 结合了前两种方法。
  • Actor（演员/策略）： 负责根据当前状态做动作（像 Policy Gradient）。
  • Critic（评论家/价值）： 负责给演员的表现打分（像 Value-based）。
• 关键区别：
  • 注意 slide 里的细节：Value-based 学的是最优策略的价值；而 Actor-Critic 里的 Critic 学的是当前策略的价值。
  • Critic 告诉 Actor：“你刚才那一步虽然拿了分，但比平均水平低（Advantage 是负的），下次少这么干。”
• 比喻： 运动员（Actor）和教练（Critic）。运动员负责跑，教练负责看录像并告诉运动员“刚才那个弯道你跑慢了”。运动员根据教练的反馈来调整姿势。

4. Model-based RL (基于模型的 RL)#

• 核心思路：先学会物理规律，再在脑子里预演。
• 怎么做： 前面三种都是 Model-Free（无模型），也就是不关心世界是怎么运作的，只管试错。Model-based 则试图先在这个环境中学习一个世界模型（World Model）：
  • 即学习 $p(s_{t+1} | s_t, a_t)$：如果我在 $s_t$ 做 $a_t$，下一个状态会变成什么？
• 学会模型后能干嘛？
  • Planning (规划)： 既然知道世界怎么变，我就不用真去跑，直接在脑子里推算（比如 MCTS 蒙特卡洛树搜索，AlphaGo 就用了这个）。
  • Improve Policy： 在“假想”的环境里训练策略，省去了在真实世界试错的高昂成本。

Tradeoffs#

样本效率 (Sample Efficiency)#

“为了训练出一个好策略，我需要与环境交互多少次？”

1. 什么是样本效率？#

• 高效率： 只需要玩几局游戏就能学会（比如人类）。
• 低效率： 需要玩几百万、几亿局才能学会（比如早期的 AI）。
• 关键点： “Wall clock time is not the same as efficiency!”。
  • 有些算法（如 Model-based）虽然需要的样本少（玩得少），但计算量大（脑子想得多），所以跑得不一定快。
  • 有些算法（如 PPO）虽然跑得快（计算简单），但需要海量的样本。

2. 效率排行榜 (从高到低)#

1. Model-based (Shallow & Deep): 效率最高。
   • 原因： 因为它学会了世界模型，可以在“脑子里”（模拟环境）训练，不需要每次都去真实世界撞墙。
2. Off-policy Q-learning (如 DQN, SAC): 效率较高。
   • 原因： 它有 Replay Buffer（回放池），以前的经验可以反复利用，榨干每一条数据的价值。
3. Actor-Critic: 中等。
   • 介于两者之间，通常也是 Off-policy 或近端策略。
4. On-policy Policy Gradient (如 REINFORCE, PPO): 效率较低。
   • 原因： 它有“洁癖”，一旦策略更新了一点点，旧数据就作废了，必须重新去环境里采集新数据。
5. Evolutionary / Gradient-free: 效率最低。
   • 原因： 类似于“瞎猜”或者遗传算法，几乎不利用梯度信息，纯靠大量的尝试来碰运气。

稳定性与易用性 (Stability and Ease of use)#

“这个算法容易训练成功吗？会不会训练着训练着就崩了？”

1. 为什么这是个问题？(Why is any of this even a question???)#

• 监督学习 (Supervised Learning)： 非常稳定。因为由于数据是固定的，这就是在做一个简单的梯度下降，就像下山一样，总能走到谷底。
• 强化学习 (RL)： 非常不稳定。因为**“数据分布取决于策略”**。你更新了策略，数据分布就变了；数据变了，梯度就变了。这就像你在下山，但山体本身在不断地震和变形。

2. 各流派的“暴雷”风险：#

• Value Function Fitting (基于价值，如 Q-Learning):
  • 原理： 最小化 Bellman Error（拟合误差）。
  • 风险： At worst, doesn’t optimize anything. 在深度强化学习（非线性）中，Q-Learning 不保证收敛。你可能训练了一周，Loss 也没降下去，或者 Q 值发散到无穷大。
  • 痛点： 拟合误差小 $\neq$ 策略得分高。
• Model-based RL:
  • 原理： 最小化模型的预测误差（让模型更懂物理规律）。
  • 风险： 模型准 $\neq$ 策略好。
  • 即使模型只有一点点误差，经过多步推演后误差会指数级放大（Butterfly Effect），导致策略学偏。
• Policy Gradient (策略梯度):
  • 原理： 直接对目标函数（总奖励）求导。
  • 优点： 它是唯一一个真正在做“梯度下降（上升）”去优化我们想要的目标（Reward）的算法。
  • 缺点： 虽然方向是对的，但路太难走（方差极大，样本效率低）。虽然它稳定收敛，但可能收敛到一个很烂的局部最优解。

假设条件 (Assumptions)#

“这些算法对环境有什么苛刻的要求？”

1. 假设 #1: 完全可观测 (Full Observability)

   • 含义： 必须能看到环境的所有细节（像下围棋，能看到全盘）。如果像打扑克或者第一人称射击游戏（只能看到眼前），就是“部分可观测”。
   • 谁依赖它： Value-based 方法（Q-Learning）非常依赖这个。如果你看不全，状态 $s$ 就不准确，Q 值就算不对。

2. 假设 #2: 回合制学习 (Episodic Learning)

   • 含义： 假设游戏是可以重置的（有 Game Over 和 Restart）。
   • 谁依赖它： 纯 Policy Gradient 方法（如 REINFORCE）通常需要跑完一整局才能算梯度。
   • 谁无所谓： 某些 Value-based 方法可以处理连续不断的任务（Continuing tasks）。

3. 假设 #3: 连续性与平滑性 (Continuity or Smoothness)

   • 含义： 假设动作或状态是连续变化的（如机械臂的角度），而不是离散的（如上下左右）。
   • 谁依赖它： Model-based 和 连续控制的 Actor-Critic。因为它们需要求导，如果环境是不连续的、跳跃的，导数就没法求，模型也就学不了。