CS285 Lecture5 Ploicy Gradient

Ploicy algorithm#

REINFORCE#

初衷是我们并不知道初始状态$p(s_1)$ 是多少，也不知道环境转移概率$p(s_{t+1}|s_t,a_t)$ ，然后直接对期望求导的话就不能求。于是乎就有一系列数学变化来去掉这两个不知道的部分

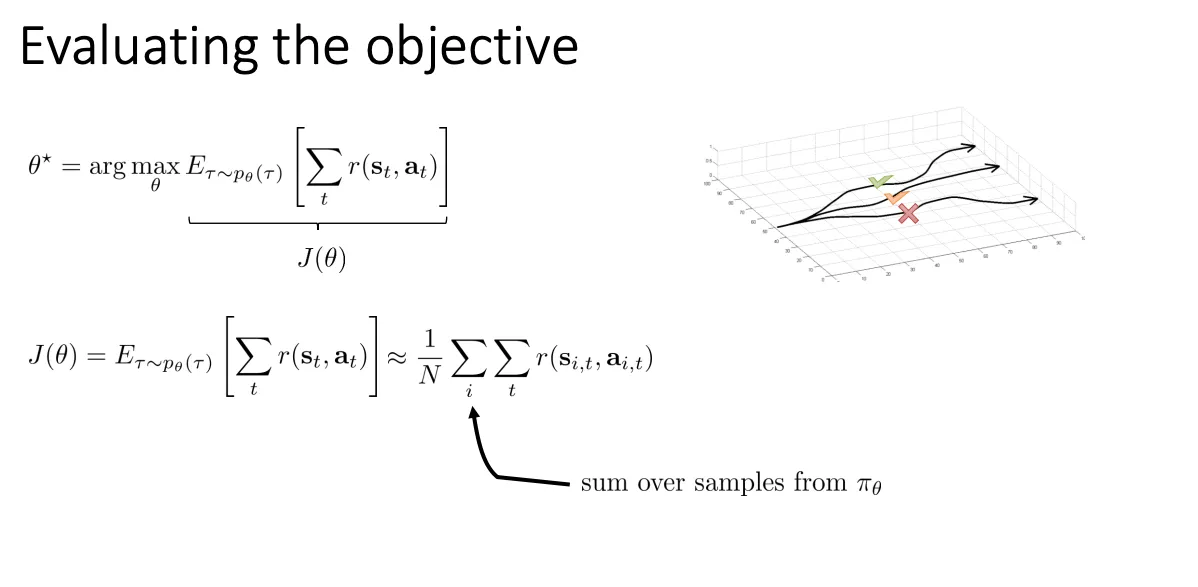
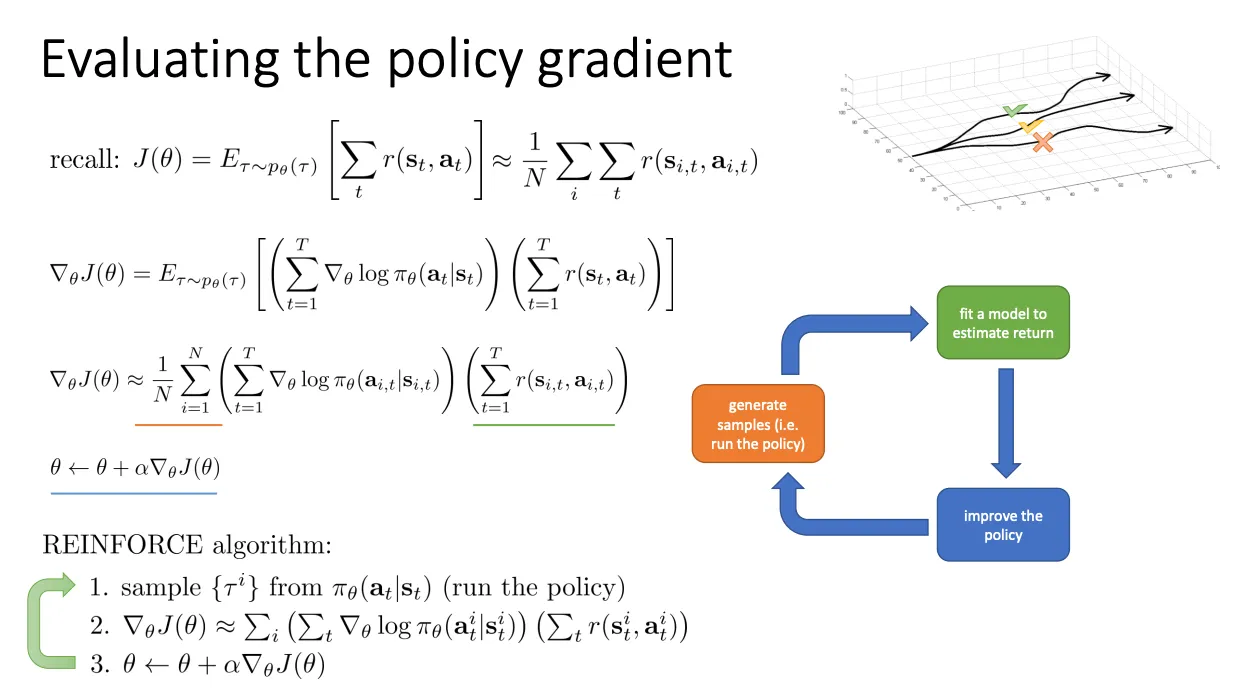
但是policy gradient有一个缺陷就是他的方差很大 $\nabla_\theta J \approx \sum (\text{梯度方向}) \times (\text{回报 } R)$

这里的 $R$ 是一个随机变量。

• 理想情况（低方差）： $R$ 总是稳定在 10 左右。那么梯度的长度就很稳定，更新很平滑。
• PG 的情况（高方差）： $R$ 可能这次是 100，下次是 -50，再下次是 500。
  • 这意味着你的梯度向量 $\nabla_\theta J$ 忽长忽短，甚至方向完全相反。
  • 神经网络的参数 $\theta$ 就会在参数空间里剧烈震荡，像个没头苍蝇一样乱撞，很难收敛到最优解。

举个例子，假如说图中绿色表示奖励，蓝色表示概率分布，那么看到当前场景，模型会尽力将概率分布从实线的变成虚线的，尽可能减小奖励为负的那部分。 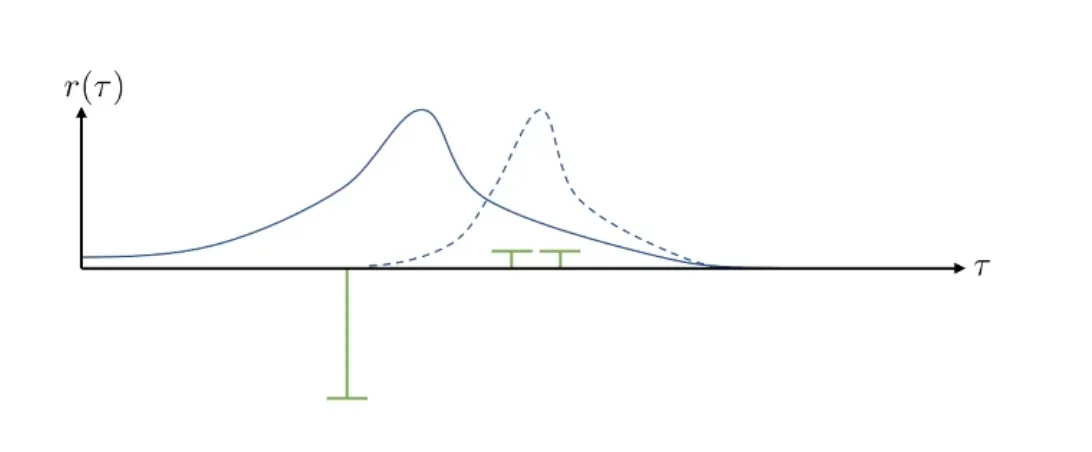但是假如我们的奖励之间的相对差没有变，但是所有的奖励都变成正数，那么模型的概率分布就又会变。 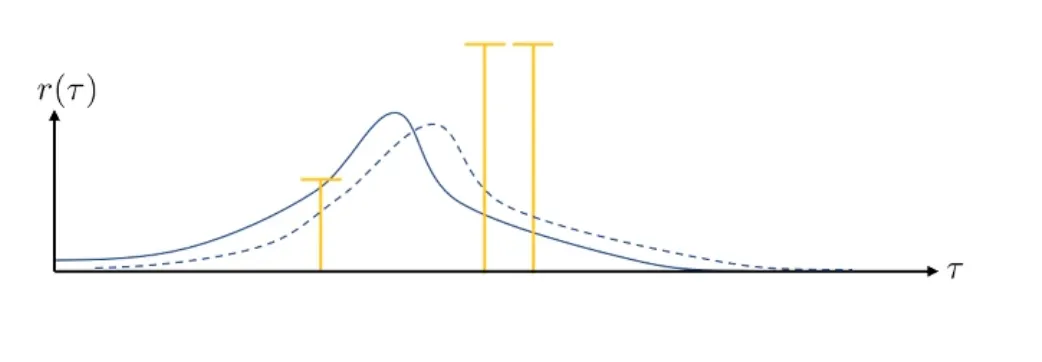也就是我们的$R$ 的波动太大，导致他的方差变大不好训练，所以可能需要大量的训练数据来根据大数定律来平均掉波动。当然还有别的方式下面会介绍。

Reducing Variance#

1#

显然的是当前的动作只会影响未来的奖励，不会影响之前的奖励，所以我们可以把红色圈中改成计算当前以及以后的奖励而不是从t=1开始计算。 这样子的好处就是减少了求和总数，必然减少方差的大小。同时他还是无偏的

证明无偏的核心思路是：

我们需要证明被减掉的那部分（即“过去的奖励”与“当前动作梯度”的乘积）在数学期望上等于 0。

如果我们证明了 $E[\text{被丢弃的项}] = 0$，那么：

$$E[\text{新公式}] = E[\text{原公式} - \text{被丢弃的项}] = E[\text{原公式}] - 0 = E[\text{原公式}]$$

既然原公式是无偏的（这是 Policy Gradient 的定义），那么新公式也就是无偏的。

下面是详细的数学推导步骤。

Score Function 的期望为 0。

对于任何概率分布 $\pi_\theta(x)$，都有：

$$E_{x \sim \pi_\theta} [\nabla_\theta \log \pi_\theta(x)] = 0$$

证明：

利用对数导数技巧 $\nabla \log f(x) = \frac{\nabla f(x)}{f(x)}$：

$$\begin{aligned} E_{x \sim \pi_\theta} [\nabla_\theta \log \pi_\theta(x)] &= \int \pi_\theta(x) \nabla_\theta \log \pi_\theta(x) \, dx \\ &= \int \pi_\theta(x) \frac{\nabla_\theta \pi_\theta(x)}{\pi_\theta(x)} \, dx \\ &= \int \nabla_\theta \pi_\theta(x) \, dx \\ &= \nabla_\theta \left( \int \pi_\theta(x) \, dx \right) \\ &= \nabla_\theta (1) \\ &= 0 \end{aligned}$$

(注：对于离散动作，积分 $\int$ 换成求和 $\sum$ 也是一样的)

结论： 只要这时候乘在这个梯度后面的是一个常数（或者不依赖于当前 $x$ 的项），整个期望就是 0。

原公式里的总回报 $\sum_{t'=1}^T r_{t'}$ 可以拆成两部分：过去的回报（Past）和未来的回报（Future/Reward-to-go）。

针对某一个特定的时刻 $t$，原公式的期望项是：

$$E \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot \left( \underbrace{\sum_{t'=1}^{t-1} r_{t'}}_{\text{过去 (Past)}} + \underbrace{\sum_{t'=t}^{T} r_{t'}}_{\text{未来 (Future)}} \right) \right]$$

利用期望的线性性质，我们可以把它拆开：

$$= \underbrace{E \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot \sum_{t'=t}^{T} r_{t'} \right]}_{\text{新公式 (PPT下半部分)}} + \underbrace{E \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot \sum_{t'=1}^{t-1} r_{t'} \right]}_{\text{我们需要证明这项为 0}}$$

我们要证明的是：

$$E \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot r_{\text{past}} \right] = 0$$

这里利用条件期望（Conditional Expectation）。

想象我们在时刻 $t$，此时状态 $s_t$ 已经确定，之前的历史（包括过去的奖励 $r_{\text{past}}$）也都已经发生了，变成了既定事实（常数）。

我们针对当前的动作 $a_t$ 求期望：

$$\begin{aligned} & E_{\text{trajectory}} \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot r_{\text{past}} \right] \\ &= E_{\text{history}} \left[ E_{a_t \sim \pi_\theta(\cdot|s_t)} \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \cdot r_{\text{past}} \mid s_t, \text{history} \right] \right] \end{aligned}$$

因果律 (Causality)

• $r_{\text{past}}$ 是在时刻 $t$ 之前发生的，它不依赖于现在才要做的动作 $a_t$。
• 所以在对 $a_t$ 求期望时，$r_{\text{past}}$ 可以像常数一样被提取出来。

$$= E_{\text{history}} \left[ r_{\text{past}} \cdot \underbrace{E_{a_t \sim \pi_\theta(\cdot|s_t)} \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \right]}_{\text{这正是我们在第1步证明的恒等式，等于 0}} \right]$$ $$= E_{\text{history}} \left[ r_{\text{past}} \cdot 0 \right] = 0$$

所以，把“过去的奖励”从公式里删掉，不会改变梯度的期望值（保持无偏），但因为少加了一堆随机数（$r_{\text{past}}$ 在不同轨迹中波动很大），所以显著降低了方差。

2#

还有方法就是给奖励设置baseline，控制奖励在一定范围内波动，最常见的应该是baseline设置为奖励的平均值。同时我们也可以计算这个变化也是无偏的。 当然我们可以设置更好的baseline值，这就要对方差进行求导。 不过在实际操作中，很少用这个。虽然这个公式是理论最优，但在深度强化学习中计算这个加权平均太麻烦了。

Off-Policy Policy Gradients#

PG一开始是on policy的，为什么呢，从这两个公式就可以看到

$$\nabla_\theta J(\theta) = \int \underbrace{p_\theta(\tau)}_{\text{这是概率分布}} \left[ \nabla_\theta \log p_\theta(\tau) r(\tau) \right] d\tau$$ $$\nabla_\theta J(\theta) = E_{\tau \sim p_\theta(\tau)} \left[ \nabla_\theta \log p_\theta(\tau) r(\tau) \right]$$

样本 $\tau$ 必须是从 $p_\theta(\tau)$ 这个分布里采样出来的

$$\tau \sim p_\theta(\tau)$$

那么就意味着每次我更新一点参数，我就要重新采集一批数据，这个是非常低效的。于是就有Off-Policy Policy Gradients。

importance sampling#

我们可以根据绿色方框中的公式变化应用到原本的训练目标中，使得

$$J(\theta) = E_{\tau \sim \bar{p}(\tau)} \left[ \frac{p_\theta(\tau)}{\bar{p}(\tau)} r(\tau) \right]$$

• $r(\tau)$：以前的回报。
• $\frac{p_\theta(\tau)}{\bar{p}(\tau)}$：修正系数。
  • 如果某条轨迹在当前策略 $p_\theta$ 下发生的概率很高，但在旧策略 $\bar{p}$ 下很低，这个系数就会很大（说明这条数据对现在很重要，要重视）。
  • 反之系数就会很小。 计算那个修正系数 $\frac{p_\theta(\tau)}{\bar{p}(\tau)}$ 看起来很难，因为轨迹 $\tau$ 包含了一堆东西：

$$p(\tau) = p(s_1) \prod \pi(a|s) p(s'|s,a)$$

这里面包含了 环境的物理规律（Dynamics） $p(s'|s,a)$，这通常是我们不知道的（比如风速怎么变、摩擦力是多少）。

但是当我们做除法时：

$$\frac{p_\theta(\tau)}{\bar{p}(\tau)} = \frac{p(s_1) \prod \pi_\theta(a|s) p(s'|s,a)}{p(s_1) \prod \bar{\pi}(a|s) p(s'|s,a)}$$

• 初始状态概率 $p(s_1)$：上下都有，消掉（红线划掉的部分）。
• 环境转移概率 $p(s'|s,a)$：客观世界规律不随你的策略改变，上下都有，消掉（红线划掉的部分）。

最终结果：

$$\frac{p_\theta(\tau)}{\bar{p}(\tau)} = \frac{\prod \pi_\theta(a_t|s_t)}{\prod \bar{\pi}(a_t|s_t)}$$

之后我们将上述技巧用在PG中 我们看最上面的公式：

$$\nabla_{\theta'} J(\theta') = E_{\tau \sim p_\theta(\tau)} \left[ \frac{p_{\theta'}(\tau)}{p_\theta(\tau)} \nabla_{\theta'} \log \pi_{\theta'}(\tau) r(\tau) \right]$$

这里有三个核心组件，我们需要把它们都按时间步 $t$ 展开：

1. 重要性权重（Importance Weight） $\frac{p_{\theta'}(\tau)}{p_\theta(\tau)}$：
   • 轨迹概率 $p(\tau) = p(s_1) \prod \pi(a|s) p(s'|s,a)$。
   • 环境动力学 $p(s'|s,a)$ 和初始分布 $p(s_1)$ 在分子分母中是一样的，直接消掉。
   • 只剩下策略的连乘：
   $$\frac{p_{\theta'}(\tau)}{p_\theta(\tau)} = \prod_{t=1}^T \frac{\pi_{\theta'}(a_t|s_t)}{\pi_{\theta}(a_t|s_t)}$$
2. 梯度项 $\nabla_{\theta'} \log \pi_{\theta'}(\tau)$：
   • 因为 $\log(\prod x) = \sum \log x$。
   • 所以整条轨迹的 log 概率梯度，等于每个时间步动作概率梯度的和：

$$\sum_{t=1}^T \nabla_{\theta'} \log \pi_{\theta'}(a_t|s_t)$$

3. 总回报 $r(\tau)$：
   • 就是所有时间步奖励的和：$\sum_{t=1}^T r(s_t, a_t)$。

当我们把上面三个展开式代回去，就得到了 PPT 中间那个长公式：

$$= E \left[ \left( \prod_{t=1}^T \frac{\pi_{\theta'}}{\pi_{\theta}} \right) \left( \sum_{t=1}^T \nabla \log \pi_{\theta'} \right) \left( \sum_{t=1}^T r \right) \right]$$

为了分析第 $t$ 个时刻的梯度 $\nabla_{\theta'} \log \pi_{\theta'}(a_t|s_t)$ 到底该乘以什么权重，我们把连乘部分拆成了两半：过去和未来。

公式变成了：

$$= E \left[ \sum_{t=1}^T \nabla_{\theta'} \log \pi_{\theta'}(a_t|s_t) \left( \underbrace{\prod_{t'=1}^{t} \frac{\pi_{\theta'}}{\pi_{\theta}}}_{\text{过去}} \right) \left( \sum r \right) \left( \underbrace{\prod_{t''=t}^{T} \frac{\pi_{\theta'}}{\pi_{\theta}}}_{\text{未来}} \right) \right]$$

必须要保留的（左边的连乘）： PPT 用箭头指出：“future actions don’t affect current weight”。

• 含义：我们在时刻 $t$ 做决定时，能不能到达这个状态 $s_t$，完全取决于过去（$1$ 到 $t$）发生了什么。
• 解释：如果新策略 $\pi_{\theta'}$ 和旧策略 $\pi_\theta$ 在过去差别很大，那么 $s_t$ 的出现概率就不一样，这个权重（Ratio）必须保留，用来修正状态分布的偏差。

右边的部分忽视掉，后面的章节会讲解为什么可以。

然后我们进一步处理转化后公式中连乘的那一项 连乘的那个比值哪怕每一项都只偏离一点点（比如 1.1 或 0.9），如果你乘上 100 步（$1.1^{100}$），这个数值就会变得巨大或者接近于零。这会让梯度计算极其不稳定（方差极大）。

我们可以根据下面这个公式

$$\prod_{k=1}^{t-1} \frac{\pi_{\theta'}(a_k|s_k)}{\pi_{\theta}(a_k|s_k)} \approx \frac{p_{\theta'}(s_t)}{p_{\theta}(s_t)}$$

转化一下

$$W_t = \underbrace{\left( \prod_{k=1}^{t-1} \frac{\pi_{\theta'}(a_k|s_k)}{\pi_{\theta}(a_k|s_k)} \right)}_{\text{Part A: 走到当前状态的概率比}} \cdot \underbrace{\left( \frac{\pi_{\theta'}(a_t|s_t)}{\pi_{\theta}(a_t|s_t)} \right)}_{\text{Part B: 当前动作的概率比}}$$

这一长串过去的动作概率比值 $\prod_{k=1}^{t-1} \dots$，决定了你有多大可能到达现在的状态 $s_t$ 然后

$$W_t \approx \frac{p_{\theta'}(s_t)}{p_{\theta}(s_t)} \cdot \frac{\pi_{\theta'}(a_t|s_t)}{\pi_{\theta}(a_t|s_t)}$$ $$\frac{\pi_{\theta'}(s)}{\pi_{\theta}(s)}=\frac{p_{\theta'}(s_t)}{p_{\theta}(s_t)}$$

然后我们假设“前面的 $t-1$ 步里，新策略和旧策略的表现完全一样，没有产生任何累积的偏差。”，这也就是ppt中划掉的那一部分。于是乎，我们将连乘那部分解决了。

Advanced Policy Gradients#

我们在使用标准梯度下降的时候公式是

$$\theta \leftarrow \theta + \alpha \nabla_\theta J(\theta)$$

但这个往往表现不好，原因就是参数空间（$\theta$）和概率分布空间（$\pi_\theta$）是不一样的。有的参数动一点点（比如方差 $\sigma$ 很小时的均值 $k$），概率分布会剧烈变化。有的参数动很大（比如方差 $\sigma$ 很大时的均值 $k$），概率分布几乎不变。如果我们不管三七二十一，对所有参数都用同样的步长 $\alpha$ 去更新，就会导致上梯度的“震荡”或“停滞”。

从数学上定义这个优化过程就是

$$\theta' \leftarrow \arg \max_{\theta'} (\theta' - \theta)^T \nabla_\theta J(\theta) \quad \text{s.t.} \quad \|\theta' - \theta\|^2 \leq \epsilon$$

怎么理解这个公式呢

目标函数：$\max_{\theta'} (\theta' - \theta)^T \nabla_\theta J(\theta)$ 这一项其实是对 $J(\theta')$ 的一阶泰勒展开（线性近似）。

• 推导逻辑： 根据泰勒展开，新位置的函数值 $J(\theta')$ 约等于：

$$J(\theta') \approx J(\theta) + (\theta' - \theta)^T \nabla_\theta J(\theta)$$

• 含义：
  • 因为 $J(\theta)$ 是常数（起点的分数值），所以我们要最大化 $J(\theta')$，就等同于最大化后面那一坨：$(\theta' - \theta)^T \nabla_\theta J(\theta)$。
  • 向量视角：这也是两个向量的点积。要让点积最大，更新方向 $(\theta' - \theta)$ 必须和 梯度方向 $\nabla_\theta J(\theta)$ 平行且同向。
  • 就是“我要沿着坡度最陡的方向往上爬。”

约束条件：$\text{s.t.} \quad \|\theta' - \theta\|^2 \leq \epsilon$ 这一项限制了更新的步长。

• 含义：
  • $\|\cdot\|^2$ 是欧几里得距离的平方。
  • $\epsilon$ 是一个很小的常数（可以理解为圆的半径）。
• “但是，我不允许你一步走太远。你只能在以当前位置为中心、半径为 $\sqrt{\epsilon}$ 的圆圈（或者球体）里面找新的落脚点。”

如果你用拉格朗日乘子法去解上面这个带约束的优化问题：

$$L = (\theta' - \theta)^T \nabla J - \lambda (\|\theta' - \theta\|^2 - \epsilon)$$

对 $\theta'$ 求导并令其为 0，你会得到结果：

$$\theta' - \theta = \frac{1}{2\lambda} \nabla_\theta J(\theta)$$

令 $\alpha = \frac{1}{2\lambda}$（学习率），这就变成了我们最熟悉的公式：

$$\theta' = \theta + \alpha \nabla_\theta J(\theta)$$

那么本质就是在欧几里得空间的一个小圆球内，寻找让目标函数线性增长最快的方向。

但是问题就是我们尝试优化的这个参数空间并不是我们的策略空间

1. 参数空间 (Parameter Space, $\Theta$)#

• 定义：这是你的神经网络（或任何模型）内部权重的集合。
• 具体样子：如果你有一个神经网络，它的所有权重和偏置组成了一个长向量 $\theta = [\theta_1, \theta_2, \dots, \theta_n]$。这个向量所在的 $n$ 维空间就是参数空间。
• 度量方式：通常用欧几里得距离（Euclidean Distance）。
  • 比如 $\theta$ 和 $\theta'$ 的距离是 $\|\theta - \theta'\|^2$。
  • 这就好比你在直角坐标系里量两个点的直线距离。
• 你可以控制这里：梯度下降算法（SGD, Adam）直接修改的就是这堆数字。

2. 策略分布空间 (Policy Distribution Space, $\Pi$)#

• 定义：这是你的智能体（Agent）在面对环境时，输出的概率分布的集合。
• 具体样子：对于每一个状态 $s$，智能体都会输出一个动作的概率分布 $\pi_\theta(a|s)$。所有可能的概率分布构成了这个空间。
• 度量方式：通常用 KL 散度（KL Divergence）。
  • 它衡量的是“两个概率分布有多不一样”。
  • 这实际上是一个弯曲的黎曼流形（Riemannian Manifold），而不是平坦的欧几里得空间。
• 你真正在乎的是这里：你并不关心 $\theta$ 是 0.1 还是 0.2，你只关心“智能体向左走的概率”是 10% 还是 90%。

3. 核心矛盾：两个空间的“映射”是扭曲的#

在标准的梯度下降（Vanilla PG）中，我们假设：参数变动一点点 $\approx$ 策略行为变动一点点。 但在强化学习里，这个假设经常完全崩溃。

• 标准梯度下降（Vanilla PG）： 它是在参数空间里走路。它说：“我要把参数 $\theta$ 挪动 0.01 的距离”。
  • 风险：它不知道这 0.01 在另一边（策略空间）意味着是“迈了一小步”还是“跳下了悬崖”。
• 自然梯度 / TRPO / PPO： 它们是在策略分布空间里走路。它说：“我要让策略的概率分布改变 0.01（KL 散度）”。
  • 做法：它会反推回参数空间——“为了让概率只变 0.01，我的参数 $\theta$ 到底应该动多少？”
    • 如果在敏感区，参数就只动 0.00001。
    • 如果在平原区，参数就大胆动 10.0。
  • 好处：稳定且高效。

于是我们可以改变约束条件，我们的优化目标还是不变

$$\theta' \leftarrow \arg \max_{\theta'} (\theta' - \theta)^T \nabla_\theta J(\theta) \quad \text{s.t.} \quad D(\pi_{\theta'}, \pi_\theta) \leq \epsilon$$

新的约束：$D(\pi_{\theta'}, \pi_\theta) \leq \epsilon$。计算的是两个概率分布的KL散度，描述两个概率分布的差距。我们约束前后两个概率分布的差距在一定范围内然后找最优解。

虽然 KL 散度很好，但它计算起来很复杂。为了在计算机里快速求解，我们需要对它进行近似。 PPT 下半部分展示了如何把 KL 散度转化为二次型（Quadratic Form）：

1. KL 散度的泰勒展开： 如果在 $\theta$ 附近对 $D_{KL}(\pi_{\theta'} || \pi_\theta)$ 进行二阶泰勒展开，你会发现：

   • 零阶项（常数）是 0（因为自己和自己的距离是 0）。
   • 一阶项（梯度）是 0（因为 KL 散度在 $\theta'=\theta$ 处取极小值）。
   • 二阶项（海森矩阵 Hessian）才是关键。

2. 引入 Fisher 信息矩阵（Matrix F）： PPT 给出了近似公式：

   $$D_{KL}(\pi_{\theta'} || \pi_\theta) \approx (\theta' - \theta)^T \mathbf{F} (\theta' - \theta)$$

   这里的 $\mathbf{F}$ 就是 Fisher Information Matrix (FIM)。 它的定义在右下角：

   $$\mathbf{F} = E_{\pi_\theta} [\nabla_\theta \log \pi_\theta(\mathbf{a}|\mathbf{s}) \nabla_\theta \log \pi_\theta(\mathbf{a}|\mathbf{s})^T]$$

可以把 $\mathbf{F}$ 理解为一个“地形校正器”或“曲率矩阵”。

• 它是 KL 散度的二阶导数：它告诉我们在当前的参数位置，策略分布对于参数变化有多敏感。
  • 如果某个方向上 $\mathbf{F}$ 的值很大（曲率大），说明参数稍微动一下，KL 散度就剧增（策略变化很大）。
  • 如果某个方向上 $\mathbf{F}$ 的值很小（曲率小），说明参数动很多，KL 散度才变一点点。

自然梯度更新（Natural Gradient Update）

如果我们把这个新的约束（$(\theta' - \theta)^T \mathbf{F} (\theta' - \theta) \leq \epsilon$）代入优化问题求解，我们会得到自然梯度更新公式：

$$\theta_{new} = \theta_{old} + \alpha \mathbf{F}^{-1} \nabla_\theta J(\theta)$$

请注意那个 $\mathbf{F}^{-1}$（Fisher 矩阵的逆）：

• 这就是 PPT 问的 “rescale”。
• 它自动抵消了地形的崎岖：
  • 在陡峭的地方（$\mathbf{F}$ 大），$\mathbf{F}^{-1}$ 会把梯度缩小，防止步子迈太大。
  • 在平坦的地方（$\mathbf{F}$ 小），$\mathbf{F}^{-1}$ 会把梯度放大，防止停滞不前。