CS285 Lecture6 Actor Critic Algorithms

原本的基础策略梯度估计方法是

然后我们把它改进一下，引入 Q 函数 为了数学上的严谨性，PPT 引入了 $Q$ 函数的概念：

• $\hat{Q}_{i,t}$：这是对在状态 $\mathbf{s}_{i,t}$ 采取动作 $\mathbf{a}_{i,t}$ 后，未来预期能拿到的奖励的估计值。
• $Q(\mathbf{s}_t, \mathbf{a}_t)$：这是真实的期望剩余回报（True expected reward-to-go）。公式为：

注意这里的t‘已经是从t开始计算了，根据Causality。然后意思就是

• $|\mathbf{s}_t, \mathbf{a}_t$：这是一个条件概率的写法。意思是“在这个前提下”——前提就是我们现在的脚正站在 $\mathbf{s}_t$，且现在的手正做动作 $\mathbf{a}_t$。这一步是确定的，已经发生了。
• $E_{\pi_\theta}$：意思是“对于这一步之后的所有步骤，我们要按照策略 $\pi_\theta$ 产生的概率分布来计算平均值”。 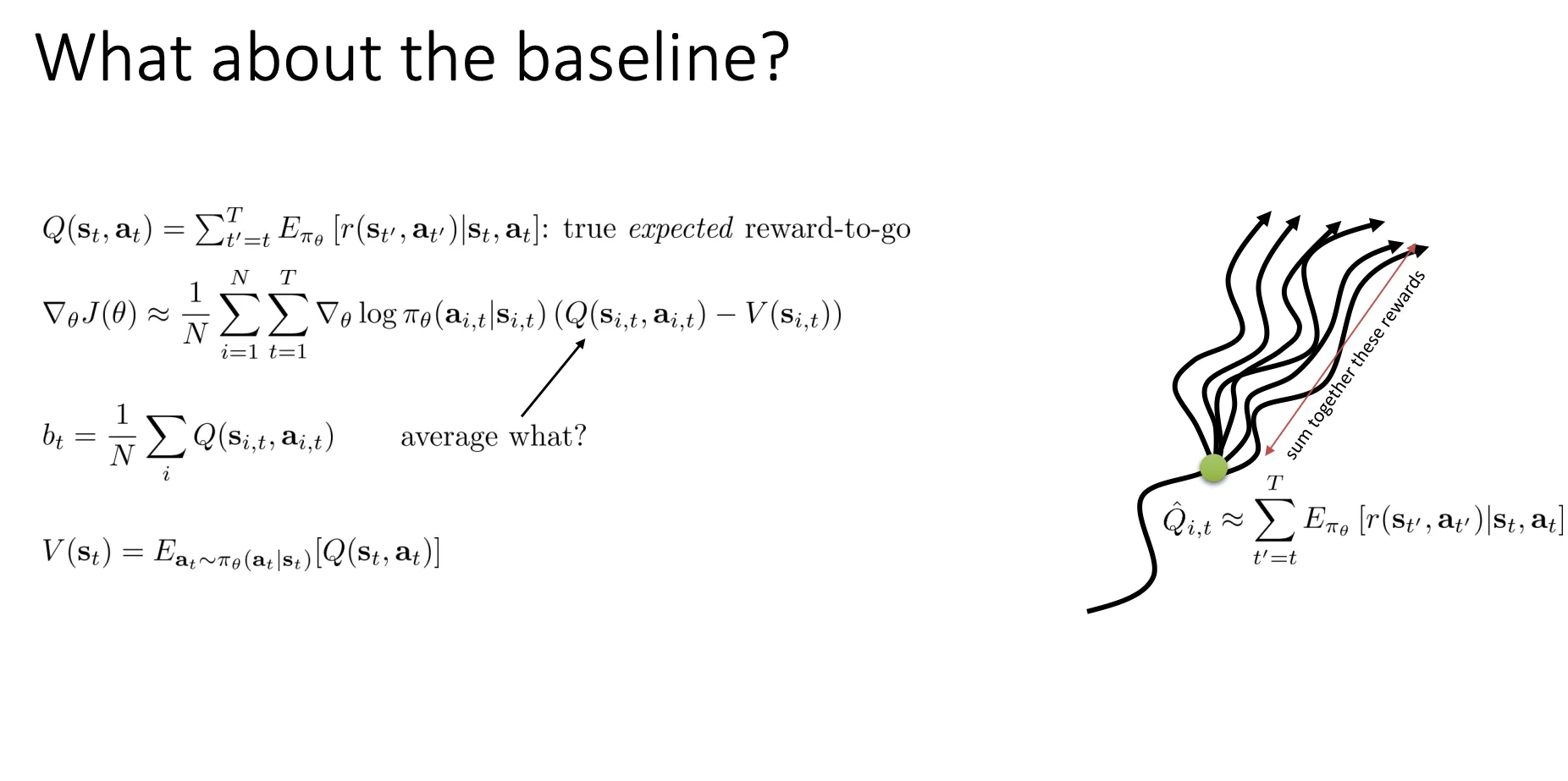改进后的公式就是这样

Q function的意思就是当前我在状态$s_t$的情况下，采取动作$a_t$之后的奖励是多少 V function的意思就是当前我在状态$s_t$的情况下,不管采取什么动作之后的平均奖励是多少

然后我们就可以参考之前的baseline的思想改进我们的公式

意义就是比较采取动作$a_t$之后的奖励和平均奖励的大小来优化模型，同时也减小方差

然后我们就可以定义$A^\pi(\mathbf{s}_t, \mathbf{a}_t)$（优势函数，Advantage Function）**：

• 公式：$A^\pi(\mathbf{s}_t, \mathbf{a}_t) = Q^\pi(\mathbf{s}_t, \mathbf{a}_t) - V^\pi(\mathbf{s}_t)$
• 含义：这步动作 $a$ 比平均水平好多少？

但是目前我们并不知道$A^\pi(\mathbf{s}_t, \mathbf{a}_t)$是多少，我们想要拟合他，

• 我们最终想求的是 $A$（优势），因为把它代入梯度公式（PPT左中位置）效果最好。
• 但是 $Q$ 和 $V$ 都是未知的。
• 利用 贝尔曼方程（Bellman Equation） 的思想，我们可以把 $Q$ 写成：

(当前的 Q 值 $\approx$ 拿到手的奖励 + 下一步局面的价值)

• 把这个代入 $A$ 的公式：

• 结论：只要我们能预测 $V^\pi(\mathbf{s})$，我们就可以算出 $Q$，进而算出 $A$。

那么问题来了：我们到底该如何计算或估计这个 $V^\pi(\mathbf{s})$ 呢？ 方法：蒙特卡洛评估 (Monte Carlo Policy Evaluation)

• 核心思想：既然我们要算“期望”（平均值），那就多试几次，然后取平均。
• 公式 1（单次采样）：

这就是说：我不知道平均分是多少，但我刚刚玩了一把，拿了 50 分，那我就暂时认为这局面的价值是 50 分。

• 公式 2（多次采样取平均）：

这就是说：为了更准一点，我从 $\mathbf{s}_t$ 开始玩 $N$ 把，把这 $N$ 把的分数加起来除以 $N$。

• 但是如果你想用上面的公式 2 准确估计某一个特定状态 $\mathbf{s}_t$ 的价值，你必须能够让时间倒流，回到 $\mathbf{s}_t$，重新玩一次，再回到 $\mathbf{s}_t$，再玩一次……

• 在现实世界中这是不可能的（你不能让机器人摔倒后，时光倒流回摔倒前的那一刻重新尝试）。

• 在模拟器中是可以的（比如游戏存盘点），但效率很低。 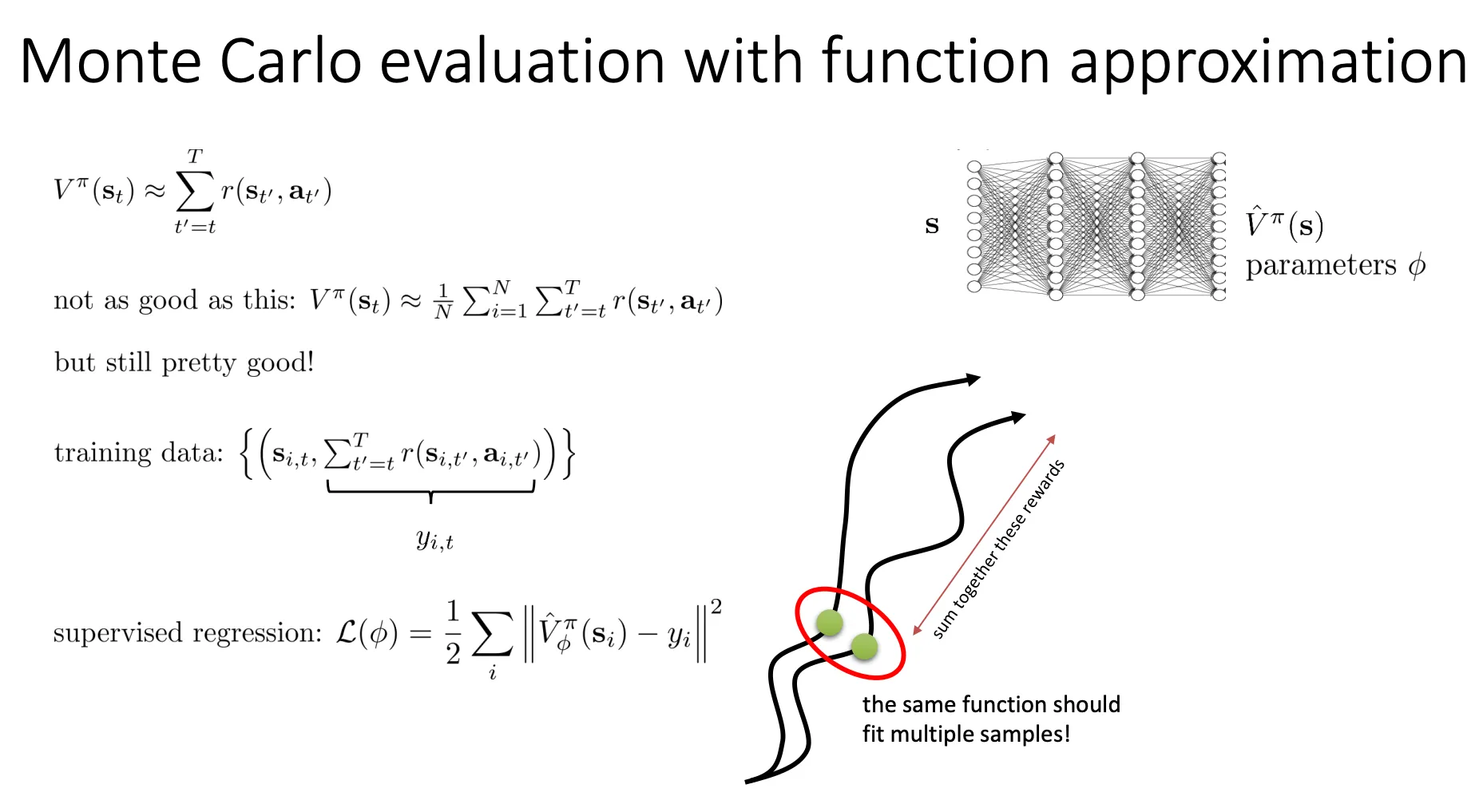然后我们训练一个神经网络来逼近这个函数， 要准确评估一个状态 $V(\mathbf{s})$，最好是从这个状态出发玩 $N$ 次取平均。但这太慢且不现实。 这张PPT提出了解决方案：

• 不追求单点完美：我们不再试图计算某一个特定状态的完美平均值。

• 依靠神经网络的泛化能力：我们收集很多次游戏的数据，然后训练一个神经网络 $\hat{V}_\phi^\pi$ 去拟合这些数据。即使每个数据点只有一次采样的结果（有噪声），神经网络也能学出整体的趋势。

• 输入（Input）：状态 $\mathbf{s}_{i,t}$。

• 标签（Label / Target）：$y_{i,t} = \sum_{t'=t}^T r(\mathbf{s}_{i,t'}, \mathbf{a}_{i,t'})$。

  • 这里的 $y_{i,t}$ 就是我们在那一次实际游戏中，从 $t$ 时刻开始一直到结束真正拿到的总分。
  • 虽然这个 $y_{i,t}$ 只是“一次”的结果（Single Sample），并不是真正的期望值（Expectation），但PPT承认它 “still pretty good”（仍然很好用）。

既然有了输入和标签，这就变成了一个标准的监督回归问题（Supervised Regression）。 PPT 下方的公式展示了训练目标：

• $\hat{V}_\phi^\pi(\mathbf{s}_i)$：神经网络当前的预测值（它认为这个状态值多少分）。
• $y_i$：实际拿到的分。
• 目标：调整网络参数 $\phi$，让预测值尽可能接近实际拿到的分（最小化均方误差）。

右下角的图非常形象地解释了为什么这样做行得通：

• 图中展示了多条黑色的轨迹（Samples）。
• 红圈圈出的部分显示，不同的轨迹可能会经过相似的状态区域。
• 这意味着，虽然我们在某一条轨迹上只看到了状态 $s$ 一次，但神经网络会通过学习成千上万条轨迹，把附近的点都“平滑”起来，从而学到一个比较准确的价值估计。

Bootstrapped#

我们还可以进一步改进 为了训练 Critic，我们要把游戏玩到底，把最后拿到的总分加起来作为标签（Label）。而这张PPT说：我们不需要等到游戏结束，可以利用 Critic 自己对下一步的预测来训练自己。

• 优点：方差显著降低。原本你要累加未来100步的随机奖励，任何一步的波动都会影响总分。现在你只看当前这一步的奖励，剩下的用一个稳定的估值代替，训练会变得非常平稳。
• 潜在风险：引入了偏差（Bias）。如果你的神经网络 $\hat{V}$ 一开始估得不准，那你算出来的标签也是错的，可能会导致误差传播。

An actor-critic algorithm#

• 有些任务是有尽头的（比如右图的机械臂堆积木，堆完就结束，称为 Episodic tasks）。但也有些任务是无限循环的（比如右图那个一直跑的小人，或者走路机器人，理论上可以永远走下去，称为 Continuous/cyclical tasks）。

• 如果任务无限长，且每一步都有正向奖励（比如只要站着不倒就 +1 分），那么你把未来的分加起来，$V$ 值就会变成无穷大（Infinitely large）。这就导致神经网络没法训练了（梯度爆炸）。 于是乎我们可以给奖励乘一个折扣因子$\gamma$ ，折扣因子 $\gamma$（比如 0.99）是每过一步乘一次。离现在越远，打折越狠。

举个例子：

• 场景：一条无限长的跑道，分成了格子：格1 $\to$ 格2 $\to$ 格3 …
• 规则：每向前走一步，得 1分奖励（$r=1$）。
• 参数：
  • 折扣因子 $\gamma = 0.9$（意味着未来的 1 分只值现在的 0.9 分）。
  • Critic 神经网络（当前状态）：刚开始训练，还有点笨，它对每个格子的价值估值得乱七八糟。

假设 Critic 目前的心理估值（预测值 $\hat{V}$）如下：

• 它觉得在 格1 的价值是 5.0 分 ($\hat{V}(s_1) = 5.0$)
• 它觉得在 格2 的价值是 4.0 分 ($\hat{V}(s_2) = 4.0$) 机器人站在 格1 ($s_1$)，决定向前走一步 ($a_1$)。
• 动作：走到 格2 ($s_2$)。
• 奖励：拿到 1 分 ($r_1=1$)。 现在我们手里有了一条数据：$\{s_1, a_1, r=1, s_2\}$。 Critic 要利用这条数据来检查自己刚才猜得准不准。
• Critic 原本的预测：我觉得站在 $s_1$ 能拿 5.0 分。
• 计算 TD Target： 实际上，我拿到了 1 分 现钞，而且我到了 $s_2$。 根据我（Critic）对 $s_2$ 的估值，未来还能拿 4.0 分，但这 4.0 分要打折。

• 结论：
  • Critic 原本以为 $s_1$ 值 5.0 分。
  • 实际走了一步后发现，基于目前的认知，$s_1$ 其实只值 4.6 分。
  • 误差 (TD Error)：$4.6 - 5.0 = -0.4$。
  • 训练 Critic：告诉神经网络，“你下次看到 $s_1$，别猜 5.0 了，往下调一点，猜 4.6 吧。”

现在来看看蒙特卡洛的情况

我们可以得到两个公式option 1和option 2 这两个公式在数学形式上非常相似，但在**“物理意义”和“训练效果”上有着本质的区别。 简单来说，差别在于：你是否认为“游戏后期的动作”比“游戏开头的动作”更不重要？ 我们来详细拆解一下：

• Option 2：

注意这里有一个 $\gamma^{t-1}$（PPT 里用红圈或者箭头特别指出的部分）。这代表第 $t$ 步的梯度，要乘上一个随时间指数级衰减的系数。

• Option 1：

这里没有 $\gamma^{t-1}$。这意味着第 1 步的梯度和第 1000 步的梯度，权重是一样的（都是 1）。

如果你严格按照“最大化初始状态的期望回报”这个数学目标去求导，你会得到 Option 2。

• 含义：它认为当下的动作最重要，未来的动作越来越不重要。

• 例子：假设 $\gamma = 0.99$。

  • 第 1 步的权重是 $1$。
  • 第 100 步的权重是 $0.99^{99} \approx 0.37$。
  • 第 1000 步的权重是 $0.99^{999} \approx 0.00004$。

• 后果：模型会极其重视开局，但几乎完全忽略后期。即使你在第 1000 步犯了一个导致“死亡”的低级错误，因为权重只有 0.00004，神经网络也懒得去改它。这会导致模型学不会处理长序列任务的后期阶段。

但是option 1我们在代码里实际使用的方法。我们人为地去掉了那个 $\gamma^{t-1}$。

• 含义：它认为无论你在第几步，只要你还活着，当下的决策就同等重要。
• 逻辑：虽然“未来的钱”要打折（计算 Reward-to-go 时依然有 $\gamma$），但是“学习的机会”不应该打折。第 1000 步的状态 $s_{1000}$ 和第 1 步的状态 $s_1$ 都是合法的状态，都需要学习最优策略。
• 后果：模型在整个游戏过程中都能均衡地学习

我们可以将这个策略运用到online的场景下，我们不收集一个batch来训练，而是每走一步我们就训练一次，实时和环境交互 Online RL (在线强化学习)这是最经典的强化学习模式。

• 定义： 智能体一边学习，一边与环境进行交互。
• 核心流程：
  1. 智能体根据当前的策略 $\pi$ 采取动作 $a$。
  2. 环境反馈新的状态 $s'$ 和奖励 $r$。
  3. 智能体利用这些新产生的数据 $(s, a, r, s')$ 来更新策略。
  4. 重复上述过程。
• 特点：
  • 数据是动态的： 随着策略的变好，智能体产生的数据分布也会发生变化。
  • 探索（Exploration）： 智能体可以主动去尝试未知的动作，以发现更好的策略。
• 缺点： 样本效率通常较低，且在真实物理环境（如昂贵的机器人或自动驾驶）中进行“试错”可能非常危险或昂贵。

Offline RL (离线强化学习)也被称为 Batch RL (虽然这两个术语在学术界有细微差别，但通常通用)。

• 定义： 智能体完全不与环境交互，仅使用一个固定的、预先收集好的静态数据集（Dataset）进行训练。

• 核心流程：

  1. 给定一个历史数据集 $\mathcal{D}$（可能由人类专家、随机策略或其他旧策略产生）。
  2. 智能体仅在 $\mathcal{D}$ 上进行训练，试图学习出一个最优策略。
  3. 训练结束后，策略才会被部署到环境中进行测试。

• 特点：

  • 数据是静态的： 训练过程中数据不会增加或改变。

  • 类似于监督学习： 流程上很像标准的 Supervised Learning，但目标是最大化累积奖励，而不仅仅是模仿数据。

  • 安全性高： 因为训练时不需要在现实世界试错。

• 主要挑战： 分布偏移 (Distributional Shift)。当智能体想要尝试一个数据集中没有的动作（OOD, Out-of-Distribution）时，由于无法通过与环境交互来验证这个动作的好坏，智能体可能会产生极其错误的乐观估计（Extrapolation Error），导致策略失效。

但是在实际应用中，每次只用一个step来进行训练对于神经网络来说并不是很好，单步更新通常方差很大，且数据相关性强。 为了解决上述的稳定性问题，PPT 展示了两种主流的并行 Actor-Critic 架构：

左图：Synchronized Parallel Actor-Critic (同步并行) -> 对应 A2C

• 工作原理：
  • 你有多个并行的环境（Worker，蓝色的竖条）。
  • Get (s, a, s’, r): 所有 Worker 同时与各自的环境交互，收集数据。
  • Wait: 系统必须等待所有 Worker 都完成这一步。
  • Update θ: 收集所有 Worker 的数据，取平均或总和，计算出一个总的梯度，然后更新全局参数。
  • 更新完后，所有 Worker 同步进入下一步。
• 特点： 协调一致，利用 GPU 批处理效率高，实现简单（通常比右边的更好用且效果不差）。

右图：Asynchronous Parallel Actor-Critic (异步并行) -> 对应 A3C

• 工作原理：
  • 有一个全局参数服务器（灰色圆柱体 $\theta$）。
  • 每个 Worker（蓝色竖条）独立运行，互不等待。
  • 当某个 Worker 收集够一定量的数据（或者完成一步），它就计算自己的梯度，异步地推送到全局服务器更新参数，并拉取最新的参数。
• 特点： 速度极快（因为不需要等待慢的 Worker），不需要 GPU 也可以在多核 CPU 上跑得很好。但由于参数更新是异步的，可能会出现“过时梯度”（Stale Gradients）的问题，导致训练有时不如 A2C 稳定。

off-policy Actor-Critic#

我们还可以使用off-policy，这样子就可以避免用完一条数据就丢弃，提高数据的利用率。 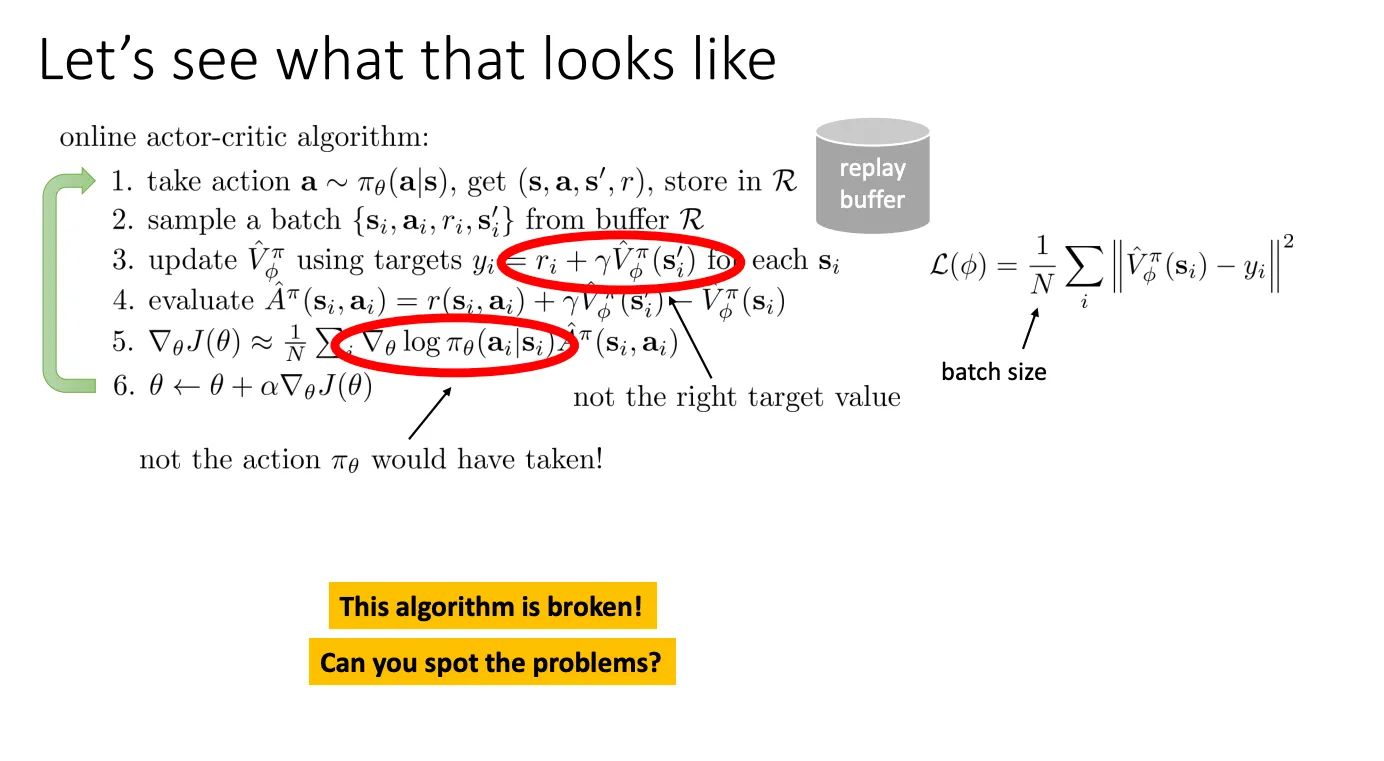思想就是每次跑新的策略得到的结果放到buffer里面，然后每次训练就从buffer里面拿一个batch来训练。

但是如果只是把这种做法嵌套进原有的框架里面会有问题

1. Critic 更新的问题 (Step 3)

• 公式含义： 这一步是在更新 Critic（价值函数 $V$），使用的是时序差分（TD）目标。

• 问题所在：
  • 定义冲突： $V^\pi(s)$ 的定义是：从状态 $s$ 出发，严格按照当前策略 $\pi$ 行动所能获得的期望回报。
  • 实际情况： 这个 $y_i$ 里的 $r_i$ 是怎么来的？它是执行了旧动作 $a_{old}$ 得到的。
  • 后果：
    • 这个 Target $y_i$ 实际上估计的是 $Q^\pi(s_i, a_{old})$（即：在状态 $s$ 强行执行旧动作 $a_{old}$，之后才遵循 $\pi$ 的价值）。
    • 如果我们直接用它来更新 $V^\pi(s)$，就会把 $V^\pi(s)$ 拉向 $Q^\pi(s, a_{old})$。
    • 除非 $a_{old}$ 恰好也是当前策略 $\pi_\theta$ 会选的动作，否则这个更新目标就是错的。这意味着 Critic 学不到当前策略的真实价值，只能学到“过去各种杂乱策略的混合价值”。

2. Actor 更新的问题 (Step 5)

• 公式含义： 这一步是在计算策略梯度 (Policy Gradient)。

• 问题所在：
  • 数学假设： 策略梯度定理要求我们在期望 $\mathbb{E}$ 中使用的样本 $(s, a)$ 必须是由当前策略 $\pi_\theta$ 产生的。也就是说，我们要问的是：“在当前策略下，这个动作好不好？”
  • 实际情况： Replay Buffer 里的 $a_i$ 是很久以前的旧策略（可能是 $\pi_{old}$）选择的。
  • 后果： 你在拿着旧策略选择的动作，强行去更新新策略的参数。
    • 例如：旧策略在 $s$ 选了 $a$，结果不错（Advantage 是正的）。公式会告诉新策略 $\pi_\theta$ ：“嘿，增加选 $a$ 的概率！”
    • 但现在的 $\pi_\theta$ 可能已经很聪明了，根本不会选 $a$，或者 $a$ 对于现在的策略来说其实是个坏动作（因为 Critic 也是旧的）。
  • 结论： 样本分布不对，算出来的梯度是有偏 (Biased) 的，甚至完全错误的。

为了解决第一个问题

• 新的写法：

• 这里的 $a'_i$ 从哪来？(核心重点)
  • PPT 用箭头特别指出：“not from replay buffer R!”
  • Buffer 里虽然存了下一步动作 $a'$，但那是“旧策略”在当时选的，我们不能用。
  • Correct Way: 我们要把 $s'_i$ 拿出来，输入给当前最新的 Actor，让它现选一个动作：

- **含义：** 虽然 $s_i$ 和 $a_i$ 是历史数据，但在计算“未来期望”时，我是用**现在的策略**去推演下一步的。这样算出来的 Target 才是属于当前策略的。然后让 $Q(s, a)$ 去拟合这个 Target。   

对于第二个问题 既然旧动作不能用，那就扔掉它，只保留旧状态。

• 保留状态 ($s_i$)：从 Replay Buffer 中拿出当时的“场景” $s_i$。
• 重采样动作 ($a_i^\pi$)：让当前的策略 $\pi_\theta$ 面对这个旧场景 $s_i$，重新做一次决策，生成一个新的动作 $a_i^\pi$

• 计算梯度：用这个新生成的动作 $a_i^\pi$ 和它对应的 Q 值 $\hat{Q}^\pi(s_i, a_i^\pi)$ 来计算梯度。
  • 注意：这里不再需要 Importance Sampling（重要性采样），因为动作本来就是从当前分布采出来的。

PPT 最下方给出了修正后的最终公式：

• 含义： 我们希望调整参数 $\theta$，使得策略 $\pi_\theta$ 更倾向于选择那些 Q 值（由 Critic 预测）高 的动作。
• 数据流变化：
  • Old: Buffer $(s, a, r, s') \rightarrow$ Update Actor using $a$.
  • New: Buffer $(s, \_, \_, \_) \rightarrow$ Sample new $a^\pi$ using Actor $\rightarrow$ Evaluate $Q(s, a^\pi)$ $\rightarrow$ Update Actor.

相比于直接使用 Buffer 里的真实回报（Return），这里我们使用了一个“采样出来的动作”加上“Critic 预测的 Q 值”来计算梯度。

• Convenient: 不需要处理复杂的 Importance Sampling 权重（那些权重容易爆炸）。
• Higher Variance: 因为我们每次算的梯度都依赖于当次随机采样的动作 $a_i^\pi$，这是一次随机估计，所以会有方差。但在大规模数据训练中，我们可以不断的输入状态s然后得到很多的a，这个过程不需要仿真获得也不需要和真实世界交互所以获取很容易，这种方差是可以被接受和平均掉的。

问题现在就是，V相比Q到底是哪里不行呢？

• $V^\pi(s)$ (状态价值)： 它的定义是：“如果不换算成具体动作，站在状态 $s$，按照策略 $\pi$ 平均能拿多少分。”
  • 数学表达：$V^\pi(s) = \sum_{a} \pi(a|s) \cdot Q^\pi(s,a)$
  • 它把策略 $\pi$ “内卷” 进了价值里。如果你换了策略（比如从 $\pi_{old}$ 换到 $\pi_{new}$），$V$ 的值本身就应该剧烈变化，因为动作分布变了。
• $Q^\pi(s, a)$ (动作价值)： 它的定义是：“在状态 $s$，强制执行动作 $a$（不管策略喜不喜欢这个动作），然后再按照策略 $\pi$ 继续走，能拿多少分。”
  • 优势： 它把第一步的动作 $a$ “固定” 了。这一步不再依赖策略的概率分布。

Critics as baselines#

State-dependent#

我们还可以把Critics当作baseline

1. Actor-Critic (最上方公式)#

这是标准的 Actor-Critic 更新方式。

• 做法： 使用 Bootstrapping（自举）。也就是用 Critic 对未来的预测 $V(s')$ 来代替真实的未来回报。
• 优点 (+ lower variance): 方差低。因为你只需要看一步真实的 $r$，剩下的都交给 Critic 预测，随机性小。
• 缺点 (- not unbiased): 有偏差。我们希望优化的目标是真实回报 $G_t$。而在 Actor-Critic 中，我们用 $r + \gamma \hat{V}(s')$ 来代替 $G_t$。

除非你的 $\hat{V}$ 完美等于真实价值函数 $V_{true}$（这在训练初期是不可能的），否则这个等式永远不成立。这个差值就是 Bias。

2. Policy Gradient (中间公式)#

这是标准的 Policy Gradient (如 REINFORCE)。

• 做法： 使用 Monte Carlo（蒙特卡洛） 回报。也就是必须等到游戏结束，把后面所有的奖励加起来作为回报。
• 优点 (+ no bias): 无偏差。因为使用的是真实发生的累计回报，数学期望上是绝对准确的。
• 缺点 (- higher variance): 方差高。因为一局游戏很长，任何一步的随机因素都会累积，导致最终的 Sum Reward 波动极大。

3. State-Dependent Baseline (最下方公式)#

这是 PPT 提出的折中方案 —— 带基线的策略梯度 (Policy Gradient with Baseline)。它试图回答：“能不能既用 Critic 降方差，又保持无偏差？”

• 做法：
  • Target 部分（被减数）： 依然使用真实的蒙特卡洛回报 $\sum r$（保持无偏差）。
  • Baseline 部分（减数）： 使用 Critic $\hat{V}(s)$ 作为一个基线减去。
• 为什么这样好？
  • + no bias: 因为 Critic 只是作为 Baseline 被减去，根据数学推导（Control Variate 理论），减去一个不依赖于动作 $a$ 的项不会改变梯度的期望方向，所以依然是无偏的。
  • + lower variance: 虽然不如第一种方法方差那么低，但因为 $\hat{V}(s)$ 能够预测回报的大致范围，减去它之后，剩下的差值（Advantage）数值会变小，从而显著降低了梯度的波动。
  • 只要 Baseline $b(s)$ 只与状态 $s$ 有关，而与动作 $a$ 无关，它对梯度的期望贡献为 0。 证明逻辑如下：

因为 $b(s)$ 和 $a$ 无关，可以提出来：

因为概率之和 $\sum \pi = 1$，常数的梯度是 0：

结论： 在第三个公式中，$\hat{V}(s)$ 只是作为一个 Baseline 被减去。根据上述证明，它在数学期望上会被抵消掉（也就是不会改变梯度的平均方向），所以它是 Unbiased（无偏） 的。它唯一的作用就是降低方差。

action-dependent#

上述的方法只是将state引入预测然后作为baseline，如果我们能用 $Q(s,a)$ 做 Baseline 呢？

• $Q(s,a)$ 是针对具体动作的预测价值。
• 如果我们计算 $Return - Q(s,a)$，理论上这个差值（Advantage）会非常小（接近于 0 或仅剩环境噪声）。
• 好处： 极大地降低方差 (Lower Variance)。
• 坏处： 直接减去 $Q(s,a)$ 会引入 Bias（偏差）。 我们的终极目标是计算 策略梯度 (Policy Gradient) 的无偏估计：

但是他方差大，所以我们引入Q作为baseline，但是这有造成他不能无偏了。 我们构造一个新的梯度估计量 $g_{new}$，利用数学恒等式：

取期望：

在这里：

• $X$ 是我们原本那个方差很大的梯度估计 $g_{target}$。
• $Y$ 是基于 Critic 的梯度估计（作为控制变量），记为 $g_{critic} = \nabla_\theta \log \pi_\theta(a|s) \cdot Q_\phi^\pi(s,a)$。 我们希望构造一个新的估计量：

如果 $g_{target}$ 和 $g_{critic}$ 高度相关（即 Critic 训练得准），那么 $(g_{target} - g_{critic})$ 的值会非常小，方差也就非常小。 带入一下就是

n-step returns#

• 方案 A: One-step Actor-Critic (只看一步)
  • 公式：$\hat{A}_C^\pi = r_t + \gamma V(s_{t+1}) - V(s_t)$
  • 特点： 也就是 TD(0)。我们只用了一个真实的奖励 $r_t$，剩下的全靠 Critic 猜。
  • 评价： 方差极低（Lower variance），但偏差很大（Higher bias），因为 Critic 总是猜不准。
• 方案 B: Monte Carlo (看到底)
  • 公式：$\hat{A}_{MC}^\pi = \sum \gamma r - V(s_t)$
  • 特点： 必须等到游戏结束，把所有奖励加起来。
  • 评价： 无偏差（No bias），但方差极高（Higher variance），因为这一路上任何一个随机扰动都会改变最终结果。 折中方案：N-step Returns (The Solution) 如果我们不只看 1 步，也不看无限步，而是看 N 步（比如 5 步或 10 步），会发生什么？
• 公式

• 含义：
  1. 你先在这个世界上真实地跑 $N$ 步，收集确凿的奖励证据（这部分是无偏的）。
  2. 跑到第 $N$ 步的时候，你累了，剩下的路程你不想跑了，于是你问 Critic：“从这儿往后还能拿多少分？”（这部分是有偏的，但因为还要乘以衰减因子 $\gamma^n$，其错误的影响被缩小了）。

右边的树状图非常生动地解释了为什么要“Cut here”（在这里截断）。

• 树根 (Start): 状态是确定的，方差很小。
• 分叉 (Branching): 每走一步，环境都会有随机性，动作也有随机性。路径像树枝一样发散。
• Bigger Variance: 走得越远，可能发生的路径组合就越多，结果的波动（方差）就越不可控。
• Cut Here:
  • 如果我们一直走到头（红色大圈），方差会爆炸。
  • 如果我们在这里切一刀（红色横线），用 Critic 的预测值来“封口”，就可以把方差控制在一个合理的范围内（Smaller variance）。

我们还可以跟进一步，我们不设定n具体是多少，我们遍历n的所有情况，然后加权累加

使用指数衰减：$w_n \propto \lambda^{n-1}$。 如果我们按照 GAE 的定义直接算，计算量会非常大且复杂。 GAE 的定义是把所有可能的 N-step 优势拿来取指数加权平均：

• 这里 $A^{(1)}$ 是只看一步的优势。
• $A^{(2)}$ 是看两步的优势。
• 以此类推……
• $(1-\lambda)$ 是为了让权重之和归一化（等于1）。

如果你直接写代码算这个，你需要先算出 $A^{(1)}$, 再算 $A^{(2)}$, 再算 $A^{(3)}$……这非常麻烦。 这里就可以有一个数学小trick 我们定义单步误差： $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$

• 看 1 步 ($A^{(1)}$):

• 看 2 步 ($A^{(2)}$):

$A^{(2)}$ 包含了 $r_t + \gamma r_{t+1} + \gamma^2 V_{t+2} - V_t$，中间的 $V_{t+1}$ 会在 $\delta$ 的相加中被消掉。

• 看 3 步 ($A^{(3)}$):

现在我们把这些 $\delta$ 代回到最开始的加权公式里

我们不要按 $A^{(n)}$ 分组，我们按 $\delta$ 分组（把所有的 $\delta_t$ 放在一起，所有的 $\delta_{t+1}$ 放在一起…）：

• $\delta_t$ 的系数是多少？ 它在每一项里都有。 系数 = $(1-\lambda) (1 + \lambda + \lambda^2 + \dots)$ 这是一个几何级数求和，$(1 + \lambda + \lambda^2 + \dots) = \frac{1}{1-\lambda}$。 所以 $\delta_t$ 的总系数 = $(1-\lambda) \cdot \frac{1}{1-\lambda} = \mathbf{1}$。
• $\delta_{t+1}$ 的系数是多少？ 它从第二项开始出现，且带着 $\gamma$。 系数 = $(1-\lambda) (\lambda \gamma + \lambda^2 \gamma + \dots)$ 提取公因数 $\gamma \lambda$，变成 $\gamma \lambda (1-\lambda)(1 + \lambda + \dots)$。 结果 = $\gamma \lambda \cdot 1 = \mathbf{\gamma \lambda}$。
• $\delta_{t+2}$ 的系数是多少？ 同理推导，结果是 $\mathbf{(\gamma \lambda)^2}$。

经过上面的运算，复杂的加权平均 $A_{GAE}$ 最终变成了极其简单的形式：

RL对数学要求太高了吧。。。。。。(悲)