CS285 Lecture7 Value Function Methods

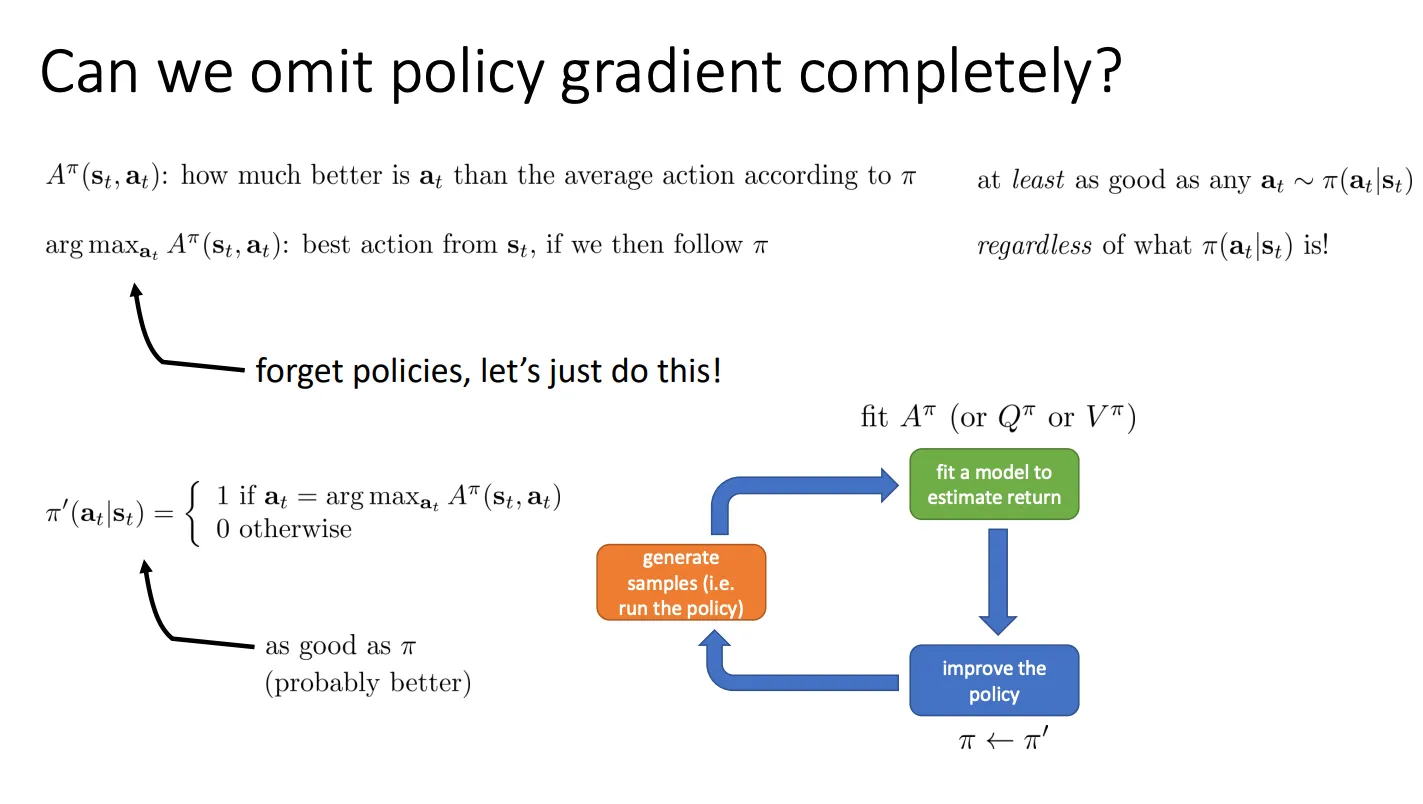
我们是否可以完全抛弃策略梯度（直接优化策略参数的方法），转而通过单纯最大化价值函数来寻找最优策略？ alt text 思路就是

既然 $A^\pi(\mathbf{s}_t, \mathbf{a}_t)$ 的意思是：在状态 $\mathbf{s}_t$ 下，采取动作 $\mathbf{a}_t$ 比当前策略 $\pi$ 的平均表现要好多少，那根据 $\arg \max_{\mathbf{a}_t} A^\pi(\mathbf{s}_t, \mathbf{a}_t)$ 那我们直接选那个优势最大（即最好的）动作

那么我们的新策略 $\pi'(\mathbf{a}_t|\mathbf{s}_t)$ 可以定义为：

如果动作 $\mathbf{a}_t$ 是优势最大的那个（argmax），则概率设为 1。
其他动作概率设为 0。

Dynamic Programming#

那么现在的问题就是怎么评估 $A^\pi(\mathbf{s}_t, \mathbf{a}_t)$ ，评估这个函数其实就是评估V，因为

A^\pi(\mathbf{s}_t, \mathbf{a}_t) \approx r(\mathbf{s}_t, \mathbf{a}_t) + V^\pi(\mathbf{s}_{t+1}) - V^\pi(\mathbf{s}_t)

在特定条件下，如何具体实现“通过价值来寻找最优策略”。这个特定方法被称为动态规划 (Dynamic Programming, DP)。 alt text 假设我们知道

$p(\mathbf{s}'|\mathbf{s}, \mathbf{a})$ ：这意味着我们要完全知道环境的模型（Model-Based）。也就是说，我们知道“如果在状态 A 做动作 B，我有多少概率会跳到状态 C”。这就像玩游戏时你手里拿着一本详细的攻略书，知道每一步的所有后果。
状态 $\mathbf{s}$ 和动作 $\mathbf{a}$ 是离散且少量的 (Discrete and small)：这意味着不需要神经网络，我们可以用简单的“表格”来存储数据。

表格型强化学习 (Tabular RL)

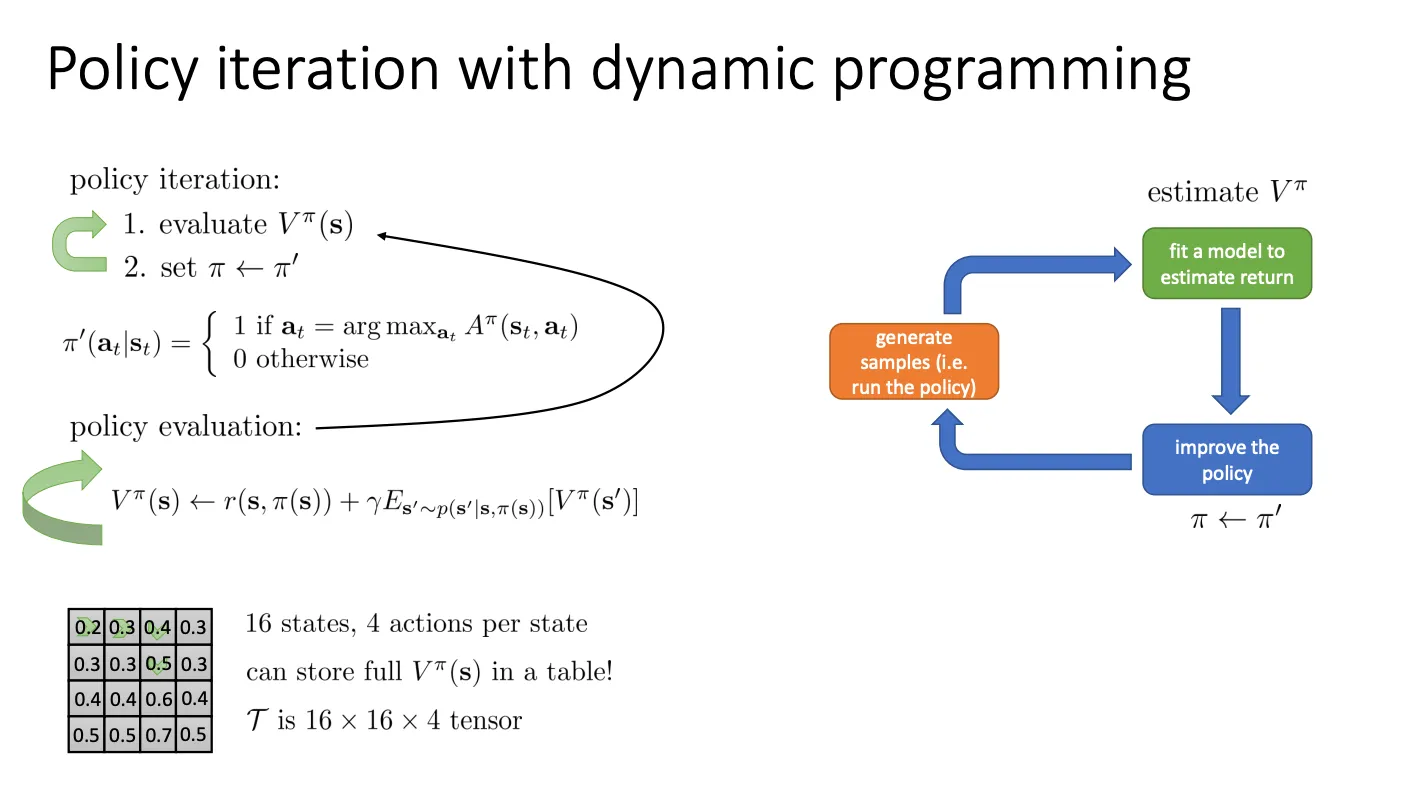
左侧的 $4 \times 4$ 网格：这是一个典型的“网格世界”示例（16个状态）。
“store full $V^\pi(\mathbf{s})$ in a table”：因为状态很少（比如只有16个），我们可以直接画一张表，把每个格子的价值 $V$ 填进去。不需要复杂的近似计算。
$\mathcal{T}$ is $16 \times 16 \times 4$ tensor：这是状态转移矩阵。意思是 16个当前状态 $\times$ 16个下一个状态 $\times$ 4个动作。这就是那个“已知的环境模型”。

更新形式就是

V^\pi(\mathbf{s}) \leftarrow E [r + \gamma E( V^\pi(\mathbf{s}'))]

由于策略是固定的，哪个价值最大我就选哪个，于是我们可以把前面的期望给省去，变成

V^\pi(\mathbf{s}) \leftarrow r + \gamma E( V^\pi(\mathbf{s}'))

于是我们的流程就变成 alt text

价值迭代算法 (The Value Iteration Algorithm)#

我们还可以进一步简化 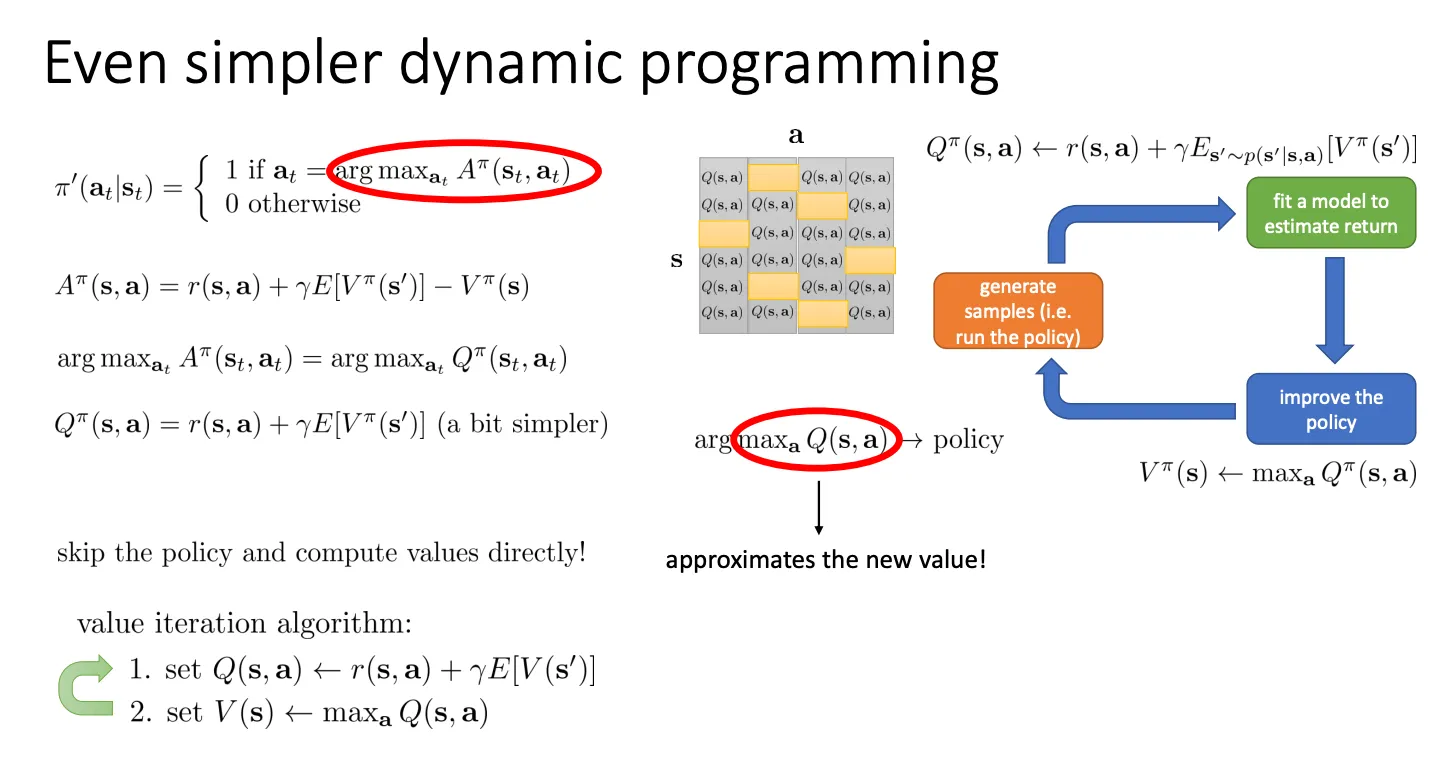alt text 既然我们想要的是 $\arg \max_{\mathbf{a}_t} A^\pi(\mathbf{s}_t, \mathbf{a}_t)$ ，这个其实就等价于 $\arg \max_{\mathbf{a}} Q^\pi(\mathbf{s}, \mathbf{a})$

\arg \max_{\mathbf{a}} A^\pi(\mathbf{s}, \mathbf{a}) = \arg \max_{\mathbf{a}} Q^\pi(\mathbf{s}, \mathbf{a})

算 Q 值：针对每一个动作，算它的即时奖励加上未来的折现价值。

Q(\mathbf{s}, \mathbf{a}) \leftarrow r(\mathbf{s}, \mathbf{a}) + \gamma E[V(\mathbf{s}')]

更新 V 值（贪婪更新）：既然算出了各个动作的 $Q$ ，那我肯定选最大的那个作为这个状态的价值 $V$ 。

V(\mathbf{s}) \leftarrow \max_{\mathbf{a}} Q(\mathbf{s}, \mathbf{a})

这个过程不断循环，直到 $V$ 值不再变化，我们就得到了最优价值函数 $V^*$ ，同时也自然拥有了最优策略（每次都选 $Q$ 最大的那个动作）。

Fitted Value Iteration#

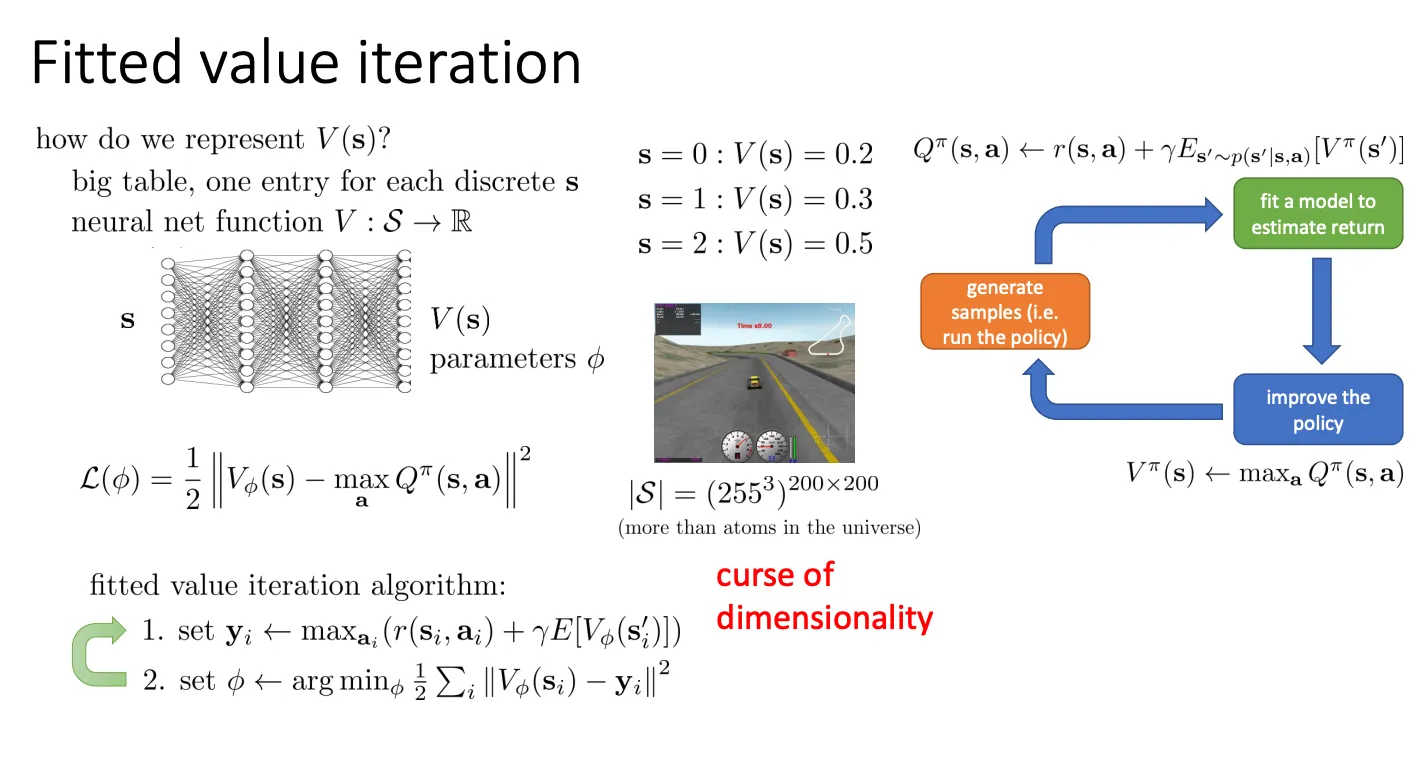alt text 我们肯定不可能维护一个Value table做出我们的决策因为你的state远远不可能用table表示完，于是乎我们就可以像之前的方法一样，用一个神经网络来预测Value，就像图中底下的部分。

但是这个算法就有一个问题，他需要我们知道转移函数 $p(\mathbf{s}'|\mathbf{s}, \mathbf{a})$ 因为第一步的期望哪里，我们从

E_{s'\sim p(s'|s,\pi(s))}[V(\mathbf{s}')]

这里的分布中计算期望

y_i \leftarrow \max_{\mathbf{a}_i} (r(\mathbf{s}_i, \mathbf{a}_i) + \gamma E[V_\phi(\mathbf{s}'_i)])

max_a：为了算出一个状态的目标价值 $y_i$ ，你需要计算所有可能动作 $\mathbf{a}_i$ 中哪个最好（Max）。
因为你不知道环境模型，你在状态 $s_i$ 只能尝试做一个动作，看到一个结果。你无法凭空知道“如果我刚才做了别的动作，结果会是什么”。

Fitted Q-Iteration#

alt text 那我们的做法就是

y_i \leftarrow r(\mathbf{s}_i, \mathbf{a}_i) + \gamma \max_{\mathbf{a}'} Q_\phi(\mathbf{s}'_i, \mathbf{a}'_i)

它用 $\max_{\mathbf{a}'} Q_\phi(\mathbf{s}'_i, \mathbf{a}'_i)$ 来近似 $E[V(\mathbf{s}'_i)]$ 。
不需要环境模型
- 第一步（现在）： $r(\mathbf{s}_i, \mathbf{a}_i)$ 是你采样（sample）得到的真实数据。
- 第二步（未来）： $\max_{\mathbf{a}'} Q_\phi(\mathbf{s}'_i, \mathbf{a}'_i)$ 是你自己对着网络（或者表格）算的。你不需要去环境里真的执行 $\mathbf{a}'$ ，你只需要问你的神经网络：“如果我在下一步状态 $\mathbf{s}'$ ，哪个动作分最高？”
- Doesn’t require simulation of actions! 这行小字就是说：我们在计算未来价值时，完全是在脑子里（神经网络里）算 Max，不需要去现实世界试错。

他最终的训练流程就是这样 alt text 这个算法是Off-Policy的，因为 $(s_i, a_i)$ 意味着如果你在状态 $s$ 做了动作 $a$ ，环境把你送到 $s'$ 并给你奖励 $r$ 。这完全是由环境的物理规则决定的（比如万有引力、游戏引擎代码），跟你是谁、你的策略 $\pi$ 是什么没有任何关系。因此，这条数据 $(s, a, s', r)$ 是一个客观事实。

同时对于 $\max_{\mathbf{a}'_i} Q_\phi(\mathbf{s}'_i, \mathbf{a}'_i)$

我们在计算目标值 $y_i$ 时，使用的是 $\max$ 操作。
这意味着：虽然在历史数据里，收集数据的人在下一步 $s'$ 可能做了一个很蠢的动作（导致死掉了），但我不管他做了什么。
我在计算价值时，假设我自己在下一步会做那个分值最高（max）的动作。
结论：我利用了你的经历（ $s, a, r, s'$ ），但我在评估未来时，抛弃了你的选择，假设了完美的未来。这就是“异策略”的本质——用别人的过去，规划自己的最优未来。

online Q-Iteration algorithm#

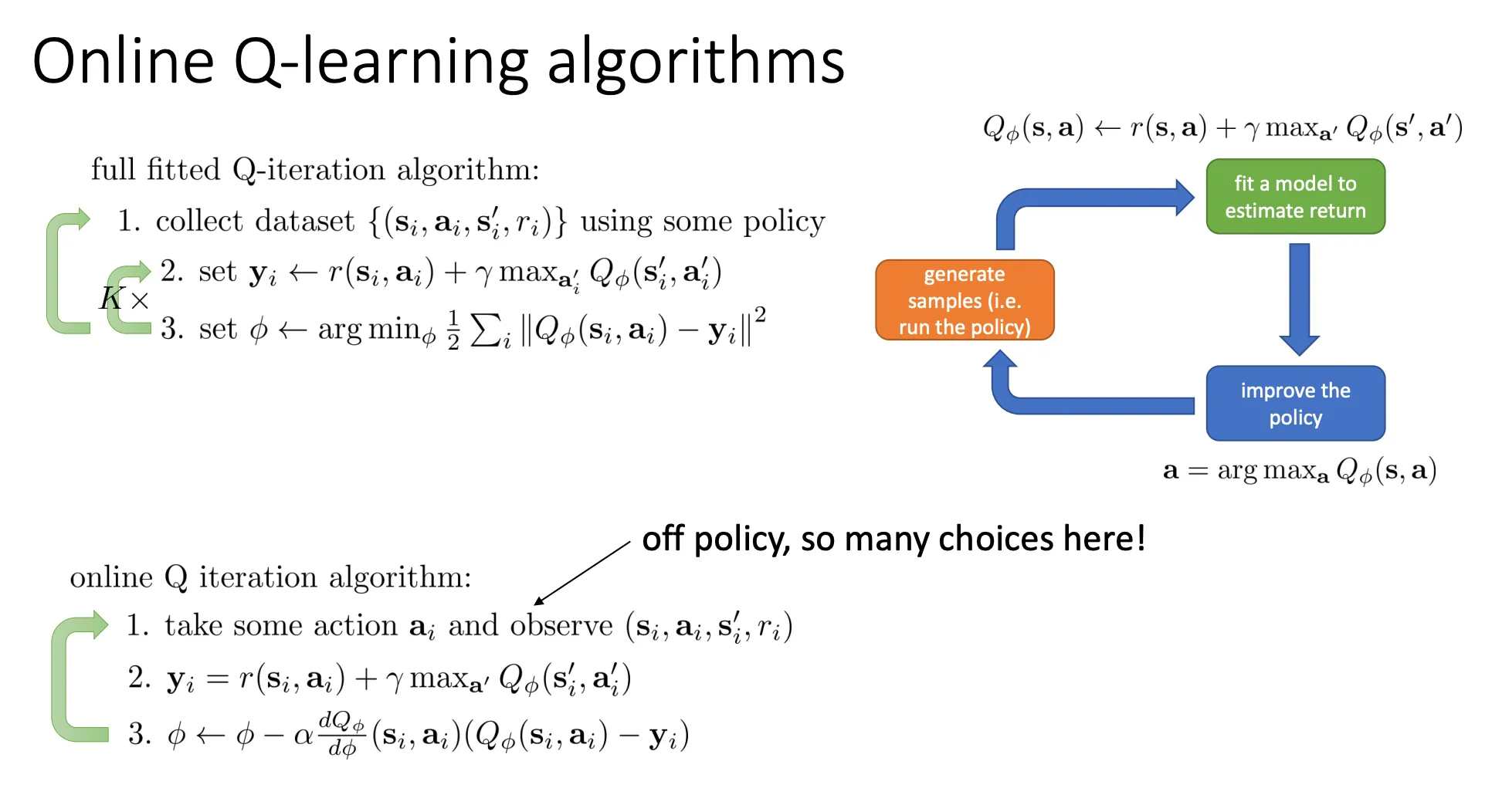alt text 我们不必非要等到收集了一大堆数据才开始训练，我们可以一收集到一条数据，就实时更新我们的神经网络。转变成online的learning

然后对于第一步，那时候我们的Q还没有训练的很好，可能还只是随机化的状态，如果此时根据贪婪策略的话，有可能会陷入局部最优

那么可以采取以下的方法

Epsilon-Greedy ( $\epsilon$ -greedy)#

这是最常用、最简单的方法。

\pi(\mathbf{a}_t|\mathbf{s}_t) = \begin{cases} 1 - \epsilon & \text{if } \mathbf{a}_t = \arg \max Q \quad \text{(利用)} \\ \epsilon / (|A| - 1) & \text{otherwise} \quad \text{(探索)} \end{cases}

机制： 扔一个骰子。
- 90% 的情况（ $1-\epsilon$ ）： 选当前认为最好的动作（Exploitation）。
- 10% 的情况（ $\epsilon$ ）： 闭着眼睛随机选一个动作（Exploration）。
好处： 保证了每一个动作都有概率被选到。甚至可以让 $\epsilon$ 在一开始的时候比较大然后随着迭代不断的减小

Boltzmann Exploration#

\pi(\mathbf{a}_t|\mathbf{s}_t) \propto \exp(Q_\phi(\mathbf{s}_t, \mathbf{a}_t))

机制： 根据 Q 值的大小来分配概率。
- Q 值越大，被选中的概率越大。
- Q 值越小，被选中的概率越小（但不是 0）。
区别：
- $\epsilon$ -greedy 是“要么最好，要么瞎选”。
- Boltzmann 是“分高的常选，分低的少选，特别差的极少选”。它比完全随机要稍微“聪明”一点。

Value Functions in Theory#

这里想讨论的是上面的这些方法其实都不收敛，下面就是证明 alt text

定义算子：

\mathcal{B}V = \max_a r_a + \gamma \mathcal{T}_a V

这里的 $\mathcal{B}$ 就是把上面的第1步和第2步合并成了一个数学操作。它把当前的价值函数向量 $V$ 映射成一个新的向量。

符号解释：
- $r_a$ (箭头指出)：是一个堆叠的向量，包含了在动作 $a$ 下所有状态的奖励。
- $\mathcal{T}_a$ (箭头指出)：是动作 $a$ $a$ 的状态转移矩阵。
  - $\mathcal{T}_{a, i, j} = p(s'=i | s=j, a)$ ：意思是在状态 $j$ 采取动作 $a$ ，跳到状态 $i$ 的概率。
- 这一行公式其实就是用矩阵乘法简洁地表达了 “即时奖励 + 转移概率 $\times$ 下一时刻价值”。
$V^*$ 是 $\mathcal{B}$ 的不动点 (Fixed Point)：

V^* = \mathcal{B}V^*

意思是：当你达到最优价值函数 $V^*$ 时，再对它应用一次算子 $\mathcal{B}$ （也就是再做一次迭代），它的值不会再改变了。

公式展开： $V^*(s) = \max_a r(s, a) + \gamma E[V^*(s')]$ 这就是著名的贝尔曼最优方程 (Bellman Optimality Equation)。 PPT 强调了 $V^*$ 的三个关键属性：

Always exists：最优价值函数一定存在。
Is always unique：它是唯一的（不管你初始值怎么设，只要收敛，终点都是这一个）。
Always corresponds to the optimal policy：一旦你求出了 $V^*$ ，你也就知道了最优策略（Optimal Policy），即每个状态下该怎么做。

虽然理论上 $V^*$ 存在且唯一，但通过不断迭代（Value Iteration）是否一定能算出来？

可以。因为贝尔曼算子 $\mathcal{B}$ 是一个 压缩映射 (Contraction Mapping)。这意味着每做一次迭代，我们离 $V^*$ 的距离就会缩小一点（按 $\gamma$ 的比例缩小），所以只要迭代次数足够多，最终一定会收敛到 $V^*$ alt text

无穷范数#

无穷范数（∞ 范数、最大范数、sup 范数）就是“看这个对象里绝对值最大的那一项”的范数。对一个向量 $x=(x1,…,x_n)$ ，无穷范数定义为 $∥x∥_∞=\max_{⁡1≤i≤n}∣xi∣$

也就是说：把所有分量的绝对值算出来，取最大的那个数。
例如 x=(2,−5,3)，则 $∥x∥_∞=5$ 。

压缩映射#

想象你手里有两张不同的价值表（两个向量），分别叫 $V$ 和 $U$ 。我们定义它们之间的“距离”为它们在所有状态中差别最大的那个值的差（无穷范数）：

||V - U||_\infty = \max_s |V(s) - U(s)|

如果算子 $\mathcal{B}$ 是压缩的，意味着：应用算子之后， $\mathcal{B}V$ 和 $\mathcal{B}U$ 之间的距离，一定要比原来的 $V$ 和 $U$ 之间的距离更小。数学表达为：

||\mathcal{B}V - \mathcal{B}U||_\infty \le \gamma ||V - U||_\infty

其中 $\gamma$ 是折扣因子，且 $0 \le \gamma < 1$ 。因为 $\gamma < 1$ ，所以距离被“压缩”了。

前面讨论的是Value Iteration中的 $\mathcal{B}$ 是压缩映射，现在迁移到fitted Value Iteration alt text 这是个监督学习 (Supervised Learning) 的过程：

第1步：生成目标 (Label Generation)

y_i \leftarrow \max_{a_i} (r(s_i, a_i) + \gamma E[V_\phi(s'_i)])

这一步计算出的 $y_i$ 其实就是 $\mathcal{B}V$ 的具体数值。
这就是我们在训练神经网络时的 “标签” (Target/Label)。
第2步：最小化误差 (Regression)

\phi \leftarrow \arg \min_\phi \frac{1}{2} \sum_i ||V_\phi(s_i) - y_i||^2

这是一个典型的 回归 (Regression) 任务。
它在调整神经网络的参数 $\phi$ ，让网络预测的输出 $V_\phi(s_i)$ 尽可能接近第1步算出来的目标 $y_i$ 。这就是数学上定义的“投影”操作（ $\Pi$ ），使用的是 L2 范数（最小二乘法）。左下角的图非常直观地解释了这个过程：
蓝线 ( $\Omega$ )：代表你的神经网络能表达的所有可能的函数的集合（假设空间）。
点 $V$ ：当前的价值函数（在蓝线上）。
点 $\mathcal{B}V$ ：应用贝尔曼公式计算出的理想目标值。注意，它不在蓝线上，说明神经网络无法完美拟合这个理想值。
点 $V'$ ：这是 $\Pi \mathcal{B}V$ 。它是蓝线上离 $\mathcal{B}V$ 最近的点。
$\Pi$ (Projection)：就是把理想的、复杂的 $\mathcal{B}V$ 强行拉回（投影）到神经网络能表示的范围内，找一个误差最小的替代品。

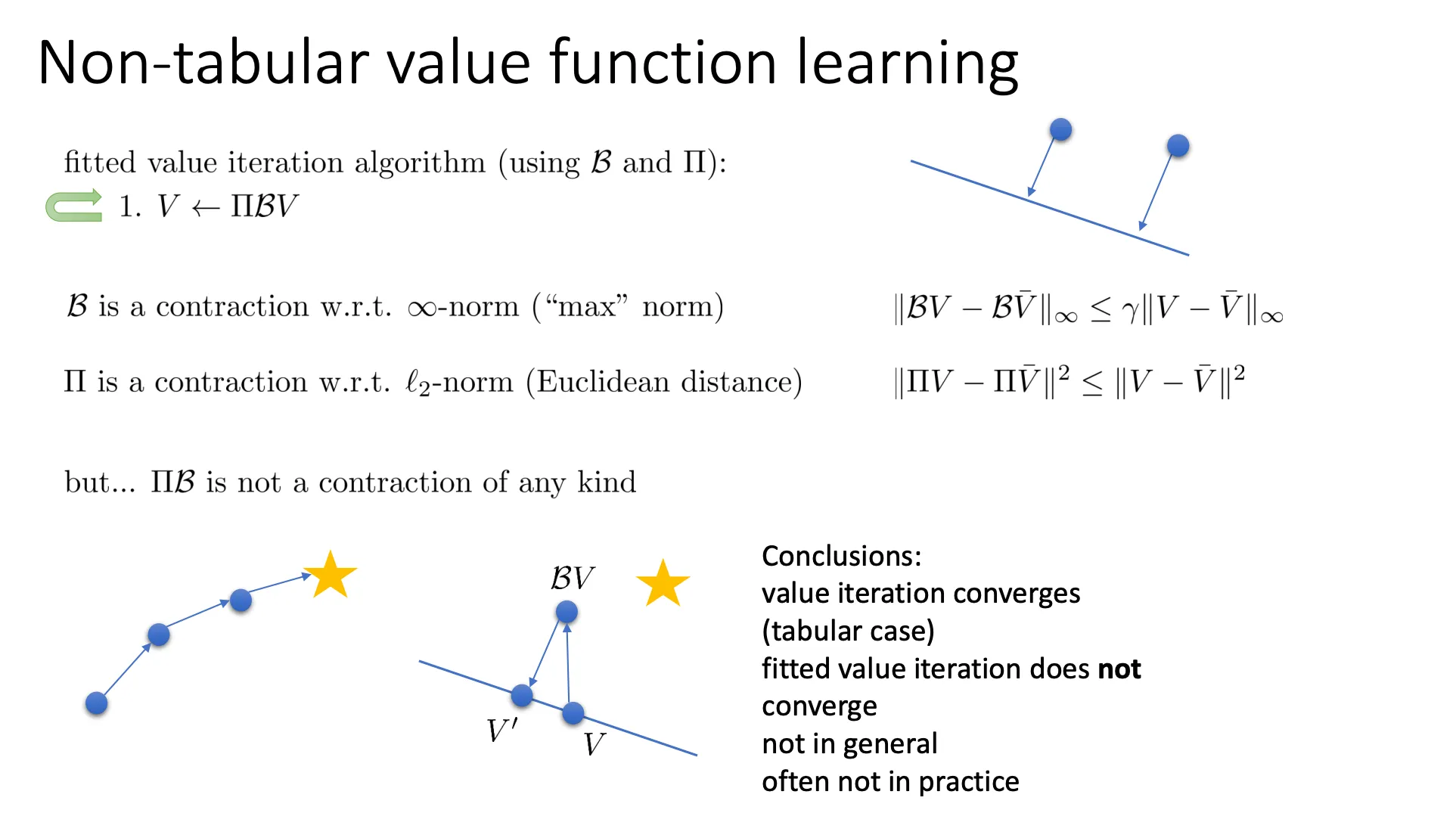alt text 然而 $\mathcal{B}$ 是压缩映射， $\Pi$ 也是压缩映射，因为两个点被投影到一条线上距离一定会小于等于原本的距离。

但是 $\Pi\mathcal{B}$ 并不一定是压缩映射，且大多情况都不是压缩映射，可以看左下角的图就是例子。

所以这也证明了为什么fitted Value Iteration并不收敛。我们还可以用同样的思路证明Q-learning也并不收敛。