CS285 Lecture8 Deep RL with Q-Functions • Laurie's Site

alt text 之前我们提到Q learning并不保证收敛，即使最后一步看着像梯度下降，但是他并不是。因为

\text{Target} = r(s, a) + \gamma \max_{a'} Q_\phi(s', a')

真正的梯度应该是：

\nabla_\phi L = (Q - \text{Target}) \cdot (\nabla_\phi Q - \nabla_\phi \text{Target})

但是第二部分我们在计算梯度时，把红圈里的项看作是一个常数。我们假装它只是一个普通的 Label，不让梯度反向传播穿过它。所以也称之为半梯度(Semi-Gradient)。

在 Online Q-learning中，Target 是不稳定的，目标值 $y_i$ 本身包含网络参数 $\phi$ ，导致你在追一个移动的靶子，从而导致很难收敛。

同时，智能体是在与环境实时交互的。每次的训练数据是高度连续的（Sequential），神经网络会发生“灾难性遗忘”（Catastrophic Forgetting）。每次神经网络只能看到局部的方框中的数据，于是当这个方框向后移动的时候，每次神经网络都会过拟合这部分，所以当这个方框走完这个轨迹的时候，神经网络只会最后的一段路，忘记前面的路径，导致在未来表现很差。 alt text 我们可以借鉴之前的思路采用同步或异步的方式去获取更多的数据来训练，就像之前的Actor-Critic Algorithms一样。

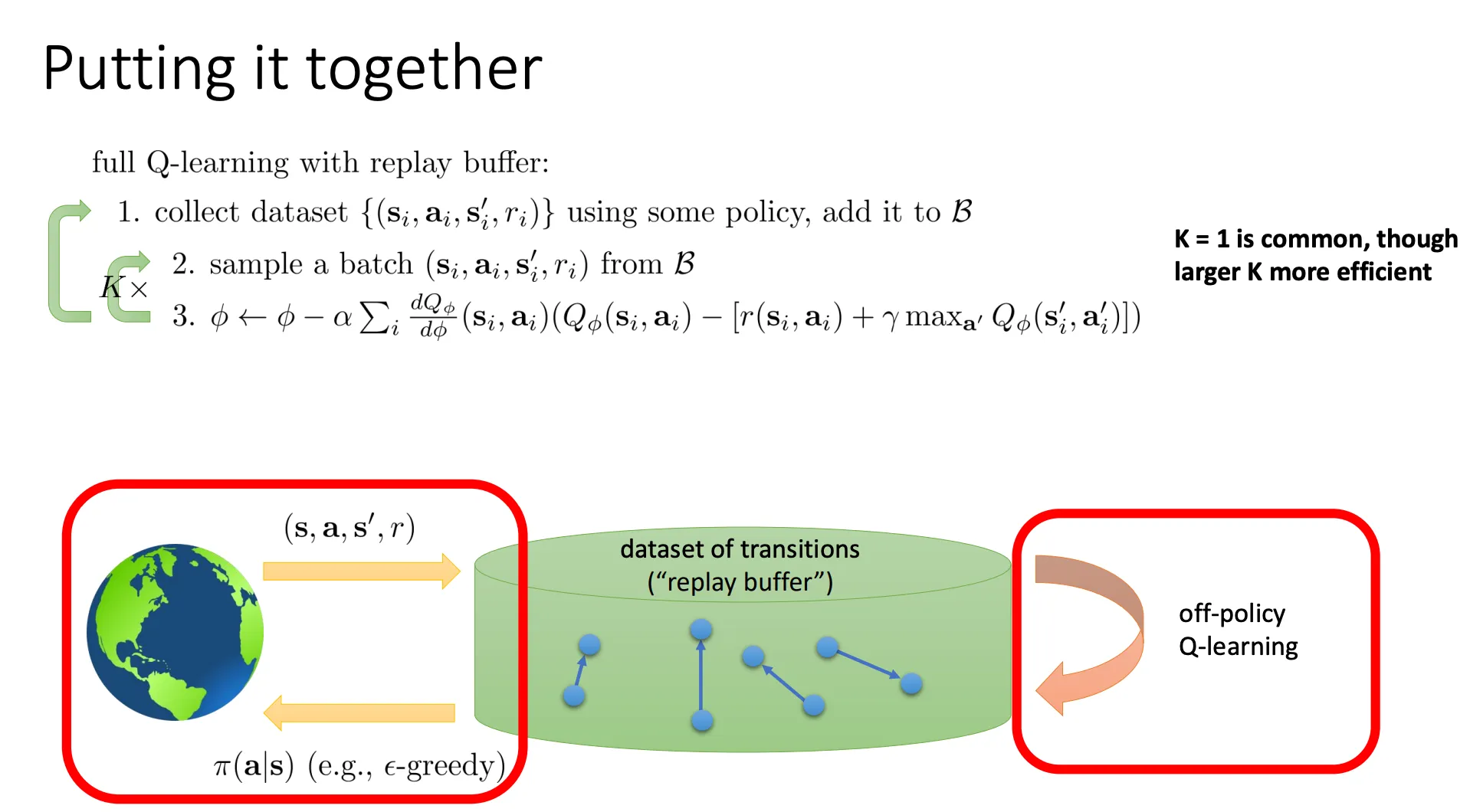
或者更好的我们也可以像之前一样用一个buffer来存数据，每次用从这个buffer里面抽一些batch来训练，这样保证了数据之间的独立同分布，然后计算梯度的时候他是一个batch的一起计算所以步骤3那里多了一个求和，这个也可以降低方差。 alt text

DQN#

我们通过buffer的方式解决了数据相关性问题，但是还有target在不断变化的问题 alt text DQN中的解决办法就是我计算目标的时候并不总是用最新的网络 $\phi$ ,而是用 $\phi'$ ，也就是我们在循环内不改变target，等到每次循环完回到第一步的时候我再改变参数

这种方法会有一定的延后(lagged)，所有就有人提出每次用 $\phi'\leftarrow \tau\phi'+(1-\tau)\phi$ 来更新
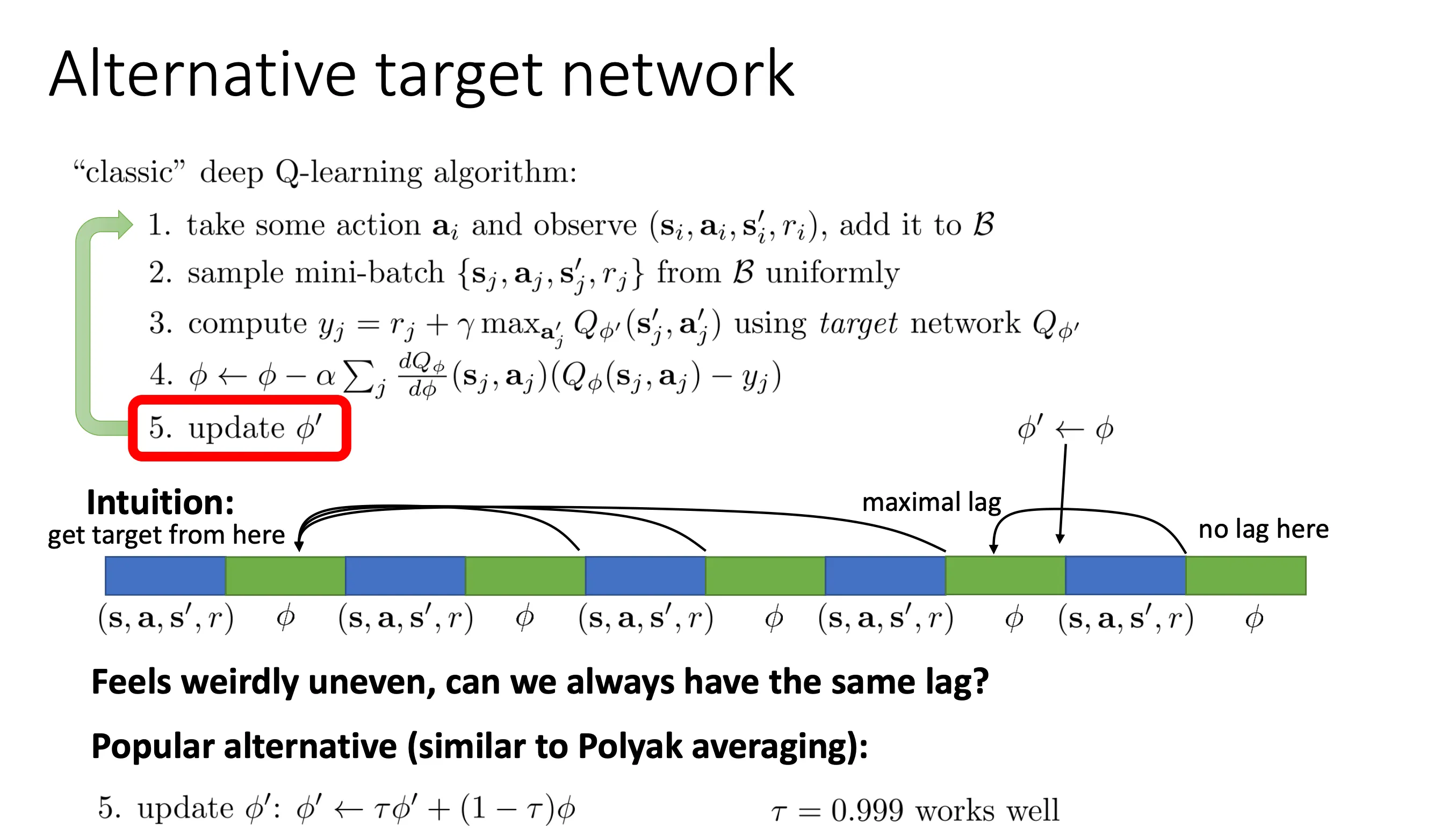
alt text

DDNQ#

alt text Q-learning中有”高估偏差”（Overestimation Bias）的问题，指的是算法对动作价值函数（Q值）产生系统性过高估计。

高估偏差的根本原因在于Q-learning更新规则中的 max 操作。当价值估计存在随机噪声时，取最大值操作（max）会倾向于选择那些被高估的Q值，而不是真实最优的值。从数学角度看，先对N个Q值取最大值再求期望，会比先求期望再取最大值得到更大的结果，这就是过估计的数学基础。

E[\max(X_1, X_2)] \ge \max(E[X_1], E[X_2])

也就是“噪声最大值的期望” 大于等于 “真实值的最大值”。

Max 操作可以分为两步

\max_{\mathbf{a}'} Q_{\phi'}(\mathbf{s}', \mathbf{a}') = Q_{\phi'}(\mathbf{s}', \underline{\arg\max_{\mathbf{a}'} Q_{\phi'}(\mathbf{s}', \mathbf{a}')})

步骤 1（下划线部分 - 选动作）： $\arg\max_{\mathbf{a}'} Q_{\phi'}(\mathbf{s}', \mathbf{a}')$
- 这就是在问：“哪个动作看起来最好？”
- PPT 注释说：“action selected according to $Q_{\phi'}$ “（根据网络 $Q_{\phi'}$ 选择动作）。
步骤 2（外层部分 - 算分数）： $Q_{\phi'}(\mathbf{s}', \dots)$
- 这就是在问：“这个被选中的动作价值多少？”
- PPT 注释说：“value also comes from $Q_{\phi'}$ “（价值也来自于网络 $Q_{\phi'}$ ）。

在标准的 Q-learning（DQN）中，你会发现上面两个步骤用的都是同一个网络参数 $\phi'$ （通常是 Target Network）。这就导致了问题：

如果网络因为噪声（Noise）错误地认为动作 A 是最好的（高估了 A），那么它不仅会选中 A（步骤 1），还会用那个高估的值作为目标（步骤 2）。
这就是 PPT 底部所说的：“these are correlated!”（噪声是相关的）。同一个网络的噪声会导致它在选动作和估值时犯同样的错误。

如何解决呢，办法就是让这两个步骤解偶，用两个模型来预测，如果这两者中的噪声是不相关的，问题就解决了 alt text 具体做法就是复用一下DNQ中的现有的两个网络（Current Network 和 Target Network）

DQN中的解决办法就是我计算目标的时候并不总是用最新的网络 $\phi$ ,而是用 $\phi'$ ，也就是我们在循环内不改变target，等到每次循环完回到第一步的时候我再改变参数

Multi-step Returns#

alt text 它的核心目的是解决强化学习中一个经典的权衡问题：偏差（Bias）与方差（Variance）的平衡。简单来说，就是我们在计算目标值（Target）时，应该“多看几步真实发生的奖励”，还是“早点依赖模型的预测”？

单步 Q-learning 的局限#

看 PPT 最上面的公式：

y_{j,t} = r_{j,t} + \gamma \max Q_{\phi'}(s_{t+1}, \dots)

如果 $Q_{\phi'}$ 很烂（Training初期）：

PPT 左边的箭头指出：“these are the only values that matter if $Q_{\phi'}$ is bad!”。意思是，如果你的神经网络（Q函数）还没训练好，它输出的值基本就是瞎猜的垃圾。这时，整个公式里唯一真实可靠的信息，只有当前的这一步奖励 $r_{j,t}$ 。剩下的部分全是误差。这会导致学习非常慢，因为真实的奖励信号传递得很慢。
偏差与方差（PPT 中间部分）：
- Q-learning (1-step): 高偏差 (Max Bias)，低方差 (Min Variance)。因为它只用了一步真实奖励，剩下全靠估计（Bootstrapping）。估计是不准的（偏差），但因为没有引入太多随机的未来路径，所以比较稳定（方差低）。
- Policy Gradient (Monte Carlo): 无偏差 (No Bias)，高方差 (High Variance)。看中间下面的公式，它用的是 $\sum \gamma^t r$ （即等到游戏结束，把所有真实奖励加起来）。这是事实数据，没有偏差，但因为每次游戏的路径都不一样，波动非常大，导致方差极高。

折衷的 Multi-step Returns#

PPT 最下方提出了问题：“Can we construct multi-step targets?”（我们可以构建多步目标吗？）答案就是底部的公式（N-step Return Estimator）：

y_{j,t} = \sum_{t'=t}^{t+N-1} \gamma^{t'-t} r_{j,t'} + \gamma^N \max Q_{\phi'}(s_{t+N}, \dots)

这个公式的意思是：我不只看 1 步，也不看直到结束，而是看 N 步。

前一部分（求和号）：我先累加接下来 $N$ 步真实发生的奖励（Real Rewards）。这部分是事实，没有偏差。
后一部分（Max Q）：在第 $N$ 步之后，我再用神经网络的预测值来作为剩下的估计。

这种方法结合了两种极端的优点：

传导更快（Faster Propagation）：想象你在一把很长的游戏中，只有最后赢了才有奖励。
- 1-step Q-learning:倒数第一步知道赢了，倒数第二步要等下一步更新才知道……奖励信号需要迭代很多次才能传到起点。
- N-step Returns: 一次更新就能把奖励信号向前回传 $N$ 步。学习效率大大提高。
准确度平衡：
- 比 1-step 准确，因为用了更多真实的 $r$ ，减少了对不可靠 Q 值的依赖（减少偏差）。
- 比 Monte Carlo 稳定，因为没有等到完全结束，减少了由于路径随机性带来的剧烈波动（控制方差）。但是他的局限就是数学上其实不满足off-policy策略，N>1 时的问题：

当你累加未来 N 步的奖励 $\sum r$ 时，你隐含地假设：“这 N 步都是按照我当前想要评估的那个策略（最优策略）走出来的。”
但在 Replay Buffer 里的历史数据中，智能体可能在第 2 步或者第 3 步做了一个愚蠢的随机动作（非最优动作）。
如果你把这个“愚蠢路径”上的奖励加起来，告诉神经网络“这就是最优策略的价值”，你就教错了

Q-Learning with Continuous Actions#

之前我们讨论的都是在离散动作的情况下，当我们想拓展到连续动作的情况下时，问题就在于 alt text max的部分对于连续的动作来说不是很好处理

Stochastic optimization#

最简单的方法就是在连续分布中采样，采样的结果就当作离散的动作，然后再运用原本的算法 alt text

Easily maximizable Q-functions#

我们还可以采用更好优化的Q函数，如果我们的Q函数很容易知道他的最大值是多少，那也可以 alt text 比如说这个工作将Q函数定义为二次函数，于是很容易就知道他的最大值是什么，但是问题就是，丧失了表达能力。因为它强制假设 Q 函数是一个单峰的二次函数（Unimodal）。但在复杂的强化学习环境中，真实的 Q 函数可能是多峰的（Multimodal），比如“向左走”和“向右走”都很好，但“中间不动”很差。NAF 无法很好地拟合这种复杂的函数形状。

DDPG#

第三种方法就是训练另一个神经网络，专门来预测哪个动作可以使Q值最大。因为 $\max_{\mathbf{a}} Q(s, a)$ 可以写为

\max_{\mathbf{a}'} Q_{\phi'}(\mathbf{s}', \mathbf{a}') = Q_{\phi'}(\mathbf{s}', \arg\max_{\mathbf{a}'} Q_{\phi'}(\mathbf{s}', \mathbf{a}'))

所以可以训练一个模型专门预测哪个动作可以使Q值最大。也就是

\mu_{\theta}(s) \approx \arg\max_{\mathbf{a}} Q_{\phi}(\mathbf{s}, \mathbf{a})

alt text 这就是DDPG算法的流程