

CS285 Lecture10 Optimal Control and Planning
CS285 Lecture10 Optimal Control and Planning
我们之前讲的都是model-free 的强化学习算法,现在转向model-base的算法。假设我们可以知道转移方程的话,我们的算法又应该怎么改进。这节课主要假设我们已经知道了准确的状态转移方程的情况下我们怎么做决策。
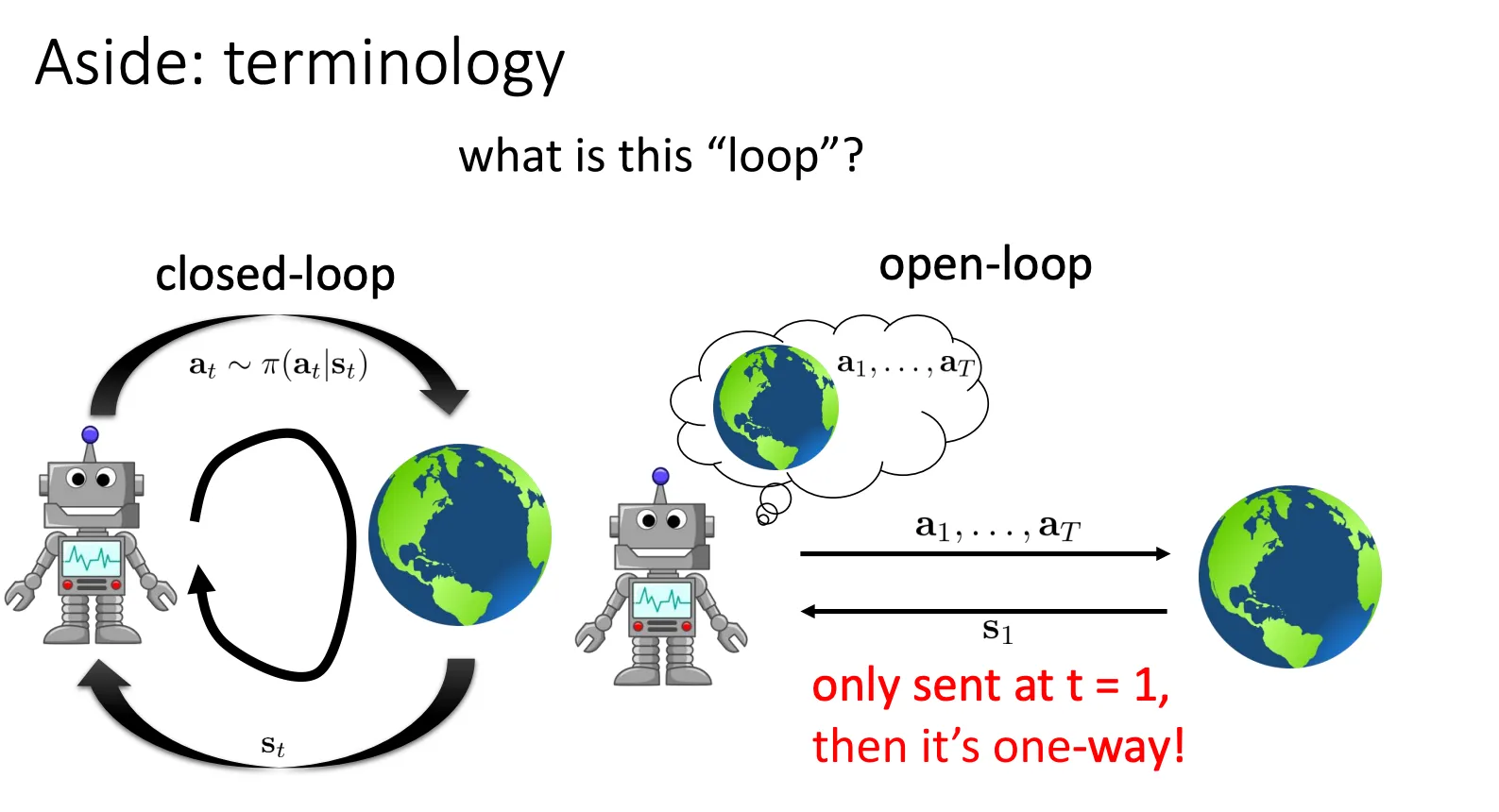 首先介绍一下两种场景,一种就是closed-loop,agent获取一个状态就做一次动作再获取状态再做一次动作,如此循环往复。与之对应的就是open-loop,获取一次状态然后做完所有的动作。
首先介绍一下两种场景,一种就是closed-loop,agent获取一个状态就做一次动作再获取状态再做一次动作,如此循环往复。与之对应的就是open-loop,获取一次状态然后做完所有的动作。
乍一看可能open-loop有什么场景,肯定不如closed-loop好,但是不一定,在某些特定的场景,维度比较低的时候,场景规律简单的时候,用这个的效果也很好。
Open-Loop Planning#
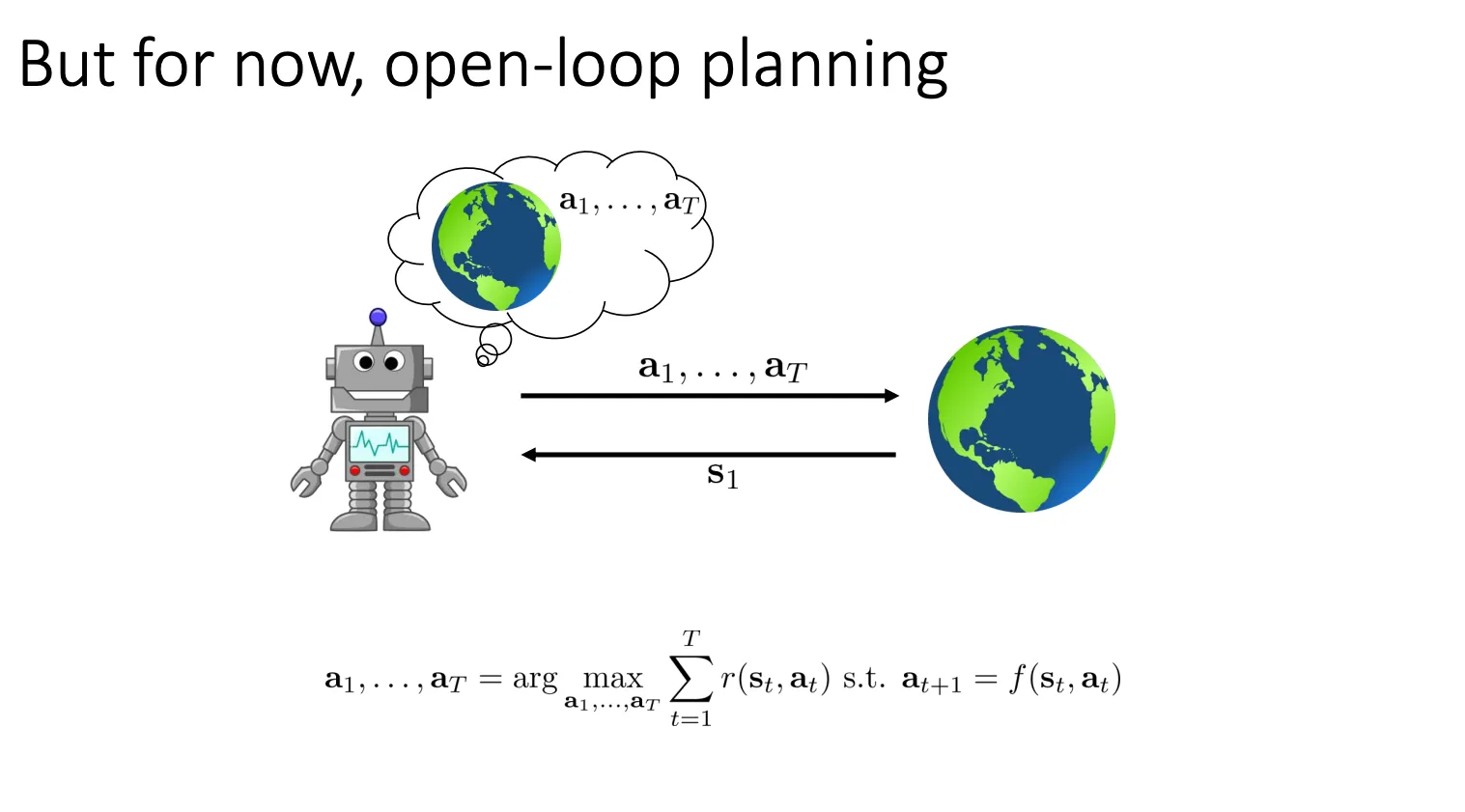 我们的目标是优化这个,找到最好的轨迹
我们的目标是优化这个,找到最好的轨迹
最简单的方法就是从一个分布中随机取一个动作序列,然后验证这个动作序列的好坏,然后最终选取抽取中最好的那个动作序列
CEM#
进阶版就是我随机取完评估之后,改变概率分布,让好的动作序列那部分的概率变大,从而可以更容易选出好的动作出来

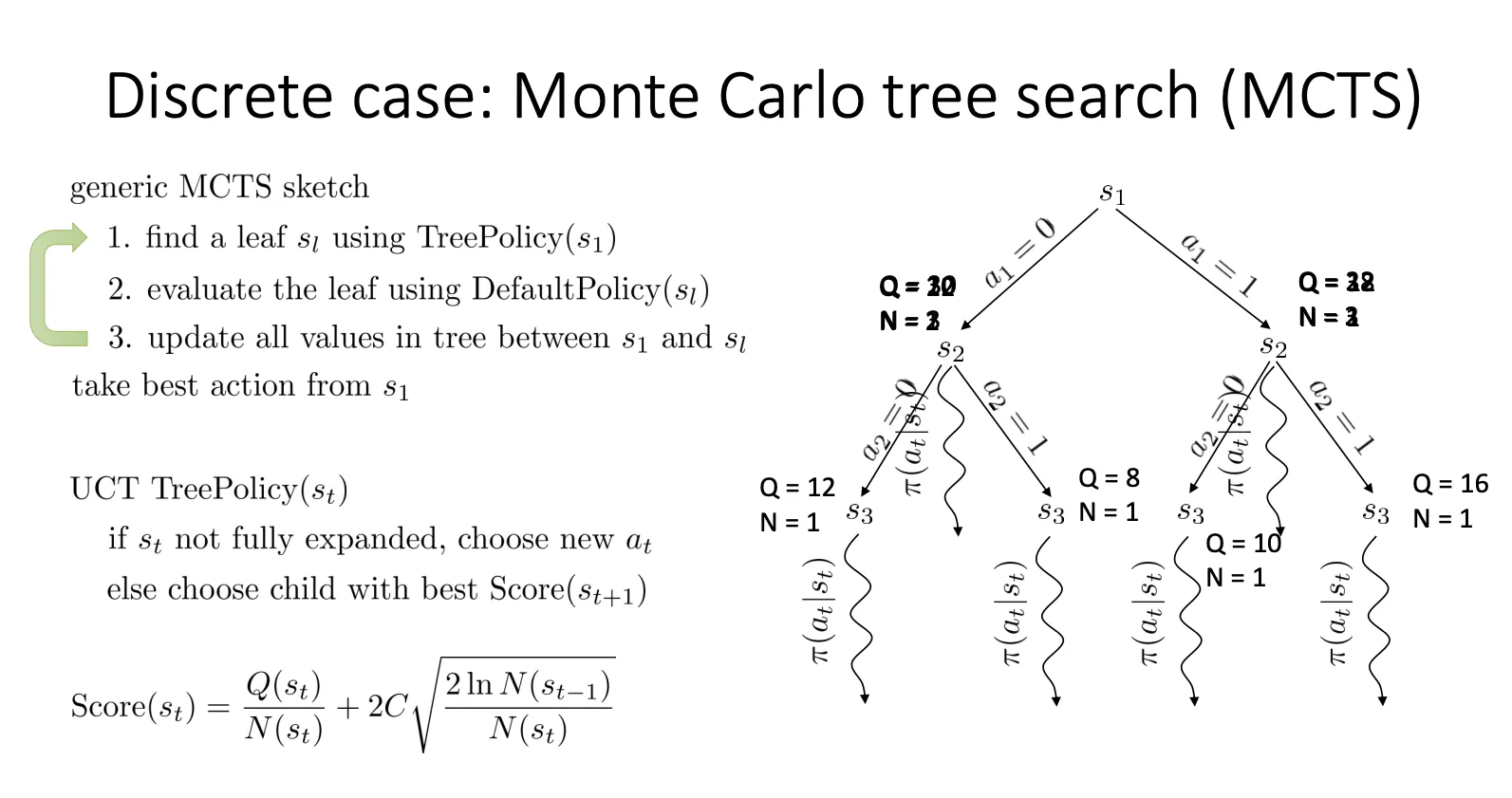
MCTS#
还可以用蒙特卡洛方法
Trajectory Optimization with Derivatives#
我们还可以用导数来优化我们的策略,主要有两种方向。
一种是shooting methods:只优化动作 (Optimize over actions only)
 另一种就是Collocation Method (配点法):优化器不仅控制动作 (Action/Control, ),还可以直接修改状态 (State, )
另一种就是Collocation Method (配点法):优化器不仅控制动作 (Action/Control, ),还可以直接修改状态 (State, )

这节课主要讲的是shooting methods
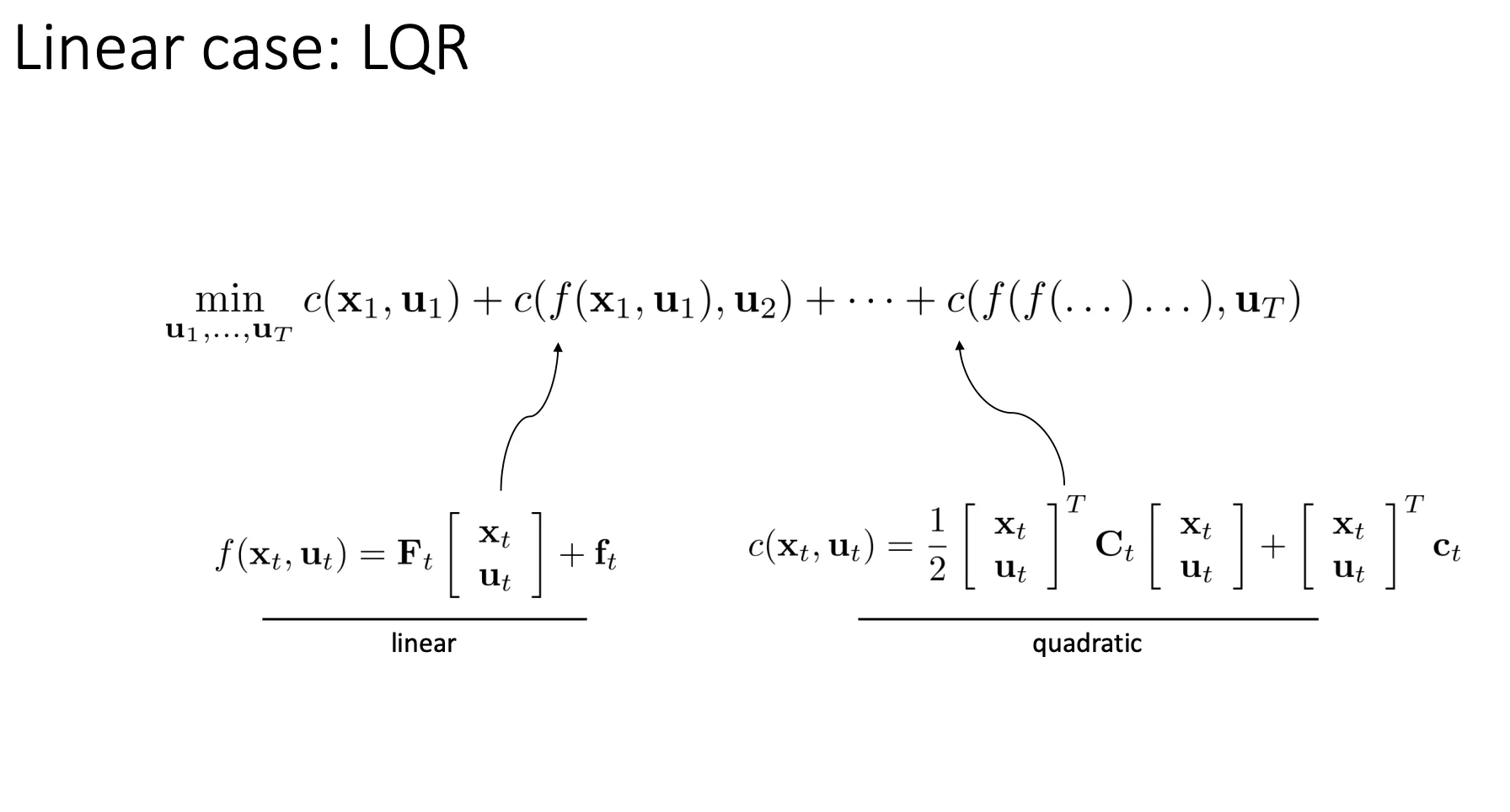
LQR#
我们对前面那个复杂的shooting methods做了一个特例化的简化,我们假设系统的物理规律是线性,然后我们的代价是一个二次型。我们来求解这种情况下的解是多少。
 为了找到最优解,我们不从 开始算,而是先看最后一步 。以下是具体的逻辑推理
为了找到最优解,我们不从 开始算,而是先看最后一步 。以下是具体的逻辑推理

我们只看最后一项然后对最后时刻的动作求导,然后解ppt下面的等式,最后用来表达
然后我们用等式替换原先的,之后化简一下,最终的cost就可以只有这一个变量表达

然后我们计算前一个时刻的cost是多少,我们知道最后时刻的是由前一时刻的和得到的,然后我们替换化简一下。前一个时刻的cost现在就变成只和和有关系
 然后我们再整理一下,他的形式就又变成了二次型,跟一开始的形式一模一样,然后我们就用同样的套路对求导,化简,于是乎这个就可以变成一个迭代的过程
然后我们再整理一下,他的形式就又变成了二次型,跟一开始的形式一模一样,然后我们就用同样的套路对求导,化简,于是乎这个就可以变成一个迭代的过程
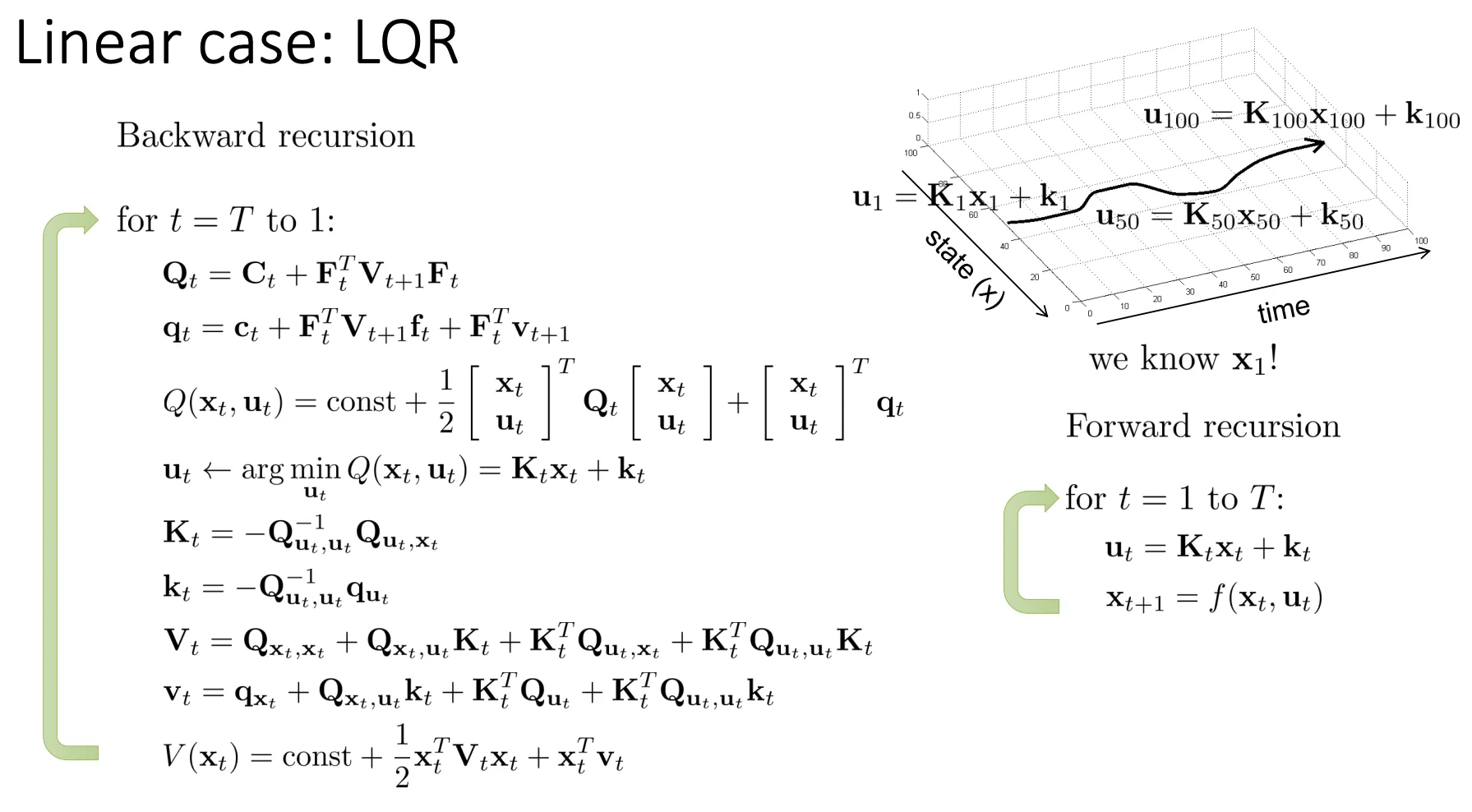
 我们可以从最后时刻一步步反推得到一开始最优的动作,然后再正推得到所有的动作,这就是LQR算法
我们可以从最后时刻一步步反推得到一开始最优的动作,然后再正推得到所有的动作,这就是LQR算法
LQR for Stochastic and Nonlinear Systems#
我们之前的假设是deterministic的而且是线形的,就是给定和,下一时刻的状态是确定的。现在拓展一下,先假设他不再是deterministic。
我们可以给他加一个高斯噪声,但是这个对于我们原先的LQR算法没有影响,可以不用变
 下面就看如果他不再是线形的,我们应该怎么改进我们的算法
下面就看如果他不再是线形的,我们应该怎么改进我们的算法
DDP/iterative LQR#
现在假设我们的不再是线形的, 不再是二次型。我们可以用泰勒展开来在局部近似成线形和二次型
 然后运行LQR
然后运行LQR

初始化 (Initialization)#
在进入循环之前,你需要先有一个初始猜测的轨迹。
- 你需要先选定一组初始的动作序列 。
- 然后用真实的非线性动力学模型 跑一遍(Rollout),得到对应的初始状态序列
- 这组 被称为标称轨迹 (Nominal Trajectory)。
迭代循环 (The Iteration Loop)#
算法的核心是一个循环,直到轨迹不再发生显著变化(收敛)为止。循环内包含三个主要步骤:
第一步:近似/线性化 (Approximation)#
在当前的标称轨迹 附近,把复杂的非线性问题简化成一个 LQR 问题。
- 计算导数:对动力学函数 和代价函数 分别求导。
- (动力学的雅可比矩阵)。
- (代价的梯度)。
- (代价的海森矩阵)。
- 构建局部模型:这一步构造出了关于偏差 () 的线性动力学方程 和二次代价函数 。
第二步:向后计算 (Backward Pass)#
利用上一步算出的矩阵 (),运行标准的 LQR 算法来规划“如何修正动作”。
- 这是一个从时间 倒推回 的过程。
- 目标:计算出每一时刻的最优反馈控制律参数 (反馈增益) 和 (前馈项)。
- 计算逻辑:
- 先算最后一步 的 。
- 利用贝尔曼方程,把 时刻的价值函数信息传递给 ,算出 。
- 一直推导到 。
第三步:向前计算 (Forward Pass)#
拿着刚才算出的控制律,在真实的非线性系统上跑一遍,生成新的轨迹。
- 更新动作:新的动作 由原来的动作加上修正量构成:
- 是开环的改进(前馈)。
- 是闭环的反馈,用来修正因为模型线性化误差导致的偏离。
- 生成新轨迹:将这个新动作输入到真实的非线性动力学 中,计算出新的状态序列。
更新与收敛 (Update & Convergence)#
- 更新:用 Forward Pass 生成的这条新轨迹,替换掉旧的标称轨迹,成为下一轮循环的起点。
- 终止:如果新轨迹和旧轨迹的代价差不多(或者梯度几乎为0),说明已经找到了局部最优解,算法结束。
然后指出iLQR是牛顿法的一种近似,如果我们也用二次展开,那么就是成了真正的全量牛顿法 (DDP)
但是牛顿法就会有一个问题
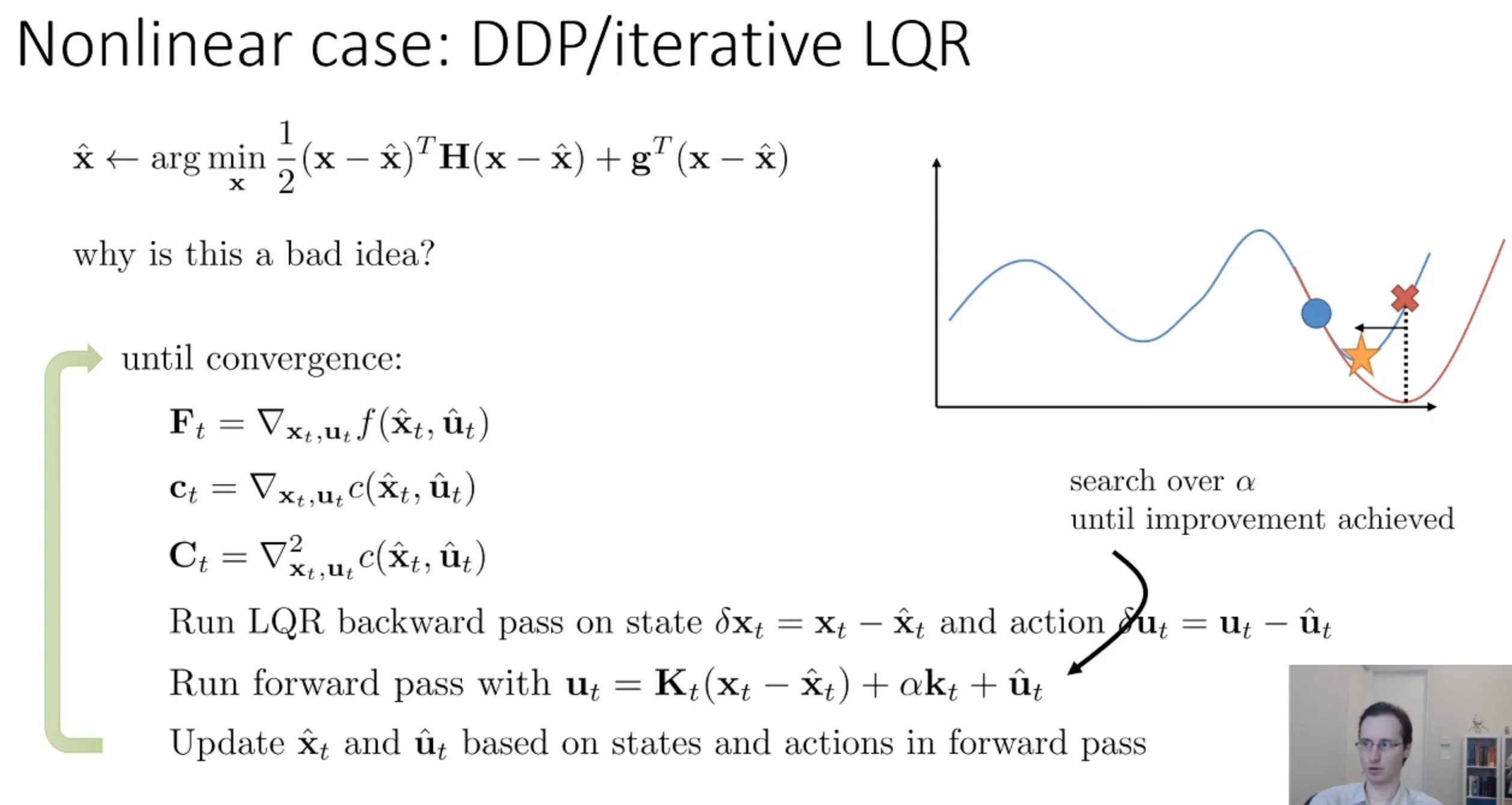 可以看左边那个图,牛顿法用二次函数对曲线进行拟合,这就有问题,我们朝着拟合的那个二次曲线优化而不是实际的蓝色那线,你会看到就有偏差,导致你的模型很难收敛。
可以看左边那个图,牛顿法用二次函数对曲线进行拟合,这就有问题,我们朝着拟合的那个二次曲线优化而不是实际的蓝色那线,你会看到就有偏差,导致你的模型很难收敛。
于是乎他在
这个公式里面加了,用来控制运动的幅度,从而解决这个问题