CS285 Lecture11 Model-Based Reinforcement Learning • Laurie's Site

这一节正式进入model-base，之前的方法是我们知道状态转移函数，但是现在我们不知道，我们需要学这个。

简单的方法就是利用监督学习那一套 alt text 但是这个方法会有分布偏移，于是可以改进一下然后这种方法一但进入到错误的动作的话，可能表现就不是很好。于是乎，还可以改进为每走一步我就重新规划一次，这样虽然增加计算量，但是他的效果会更好

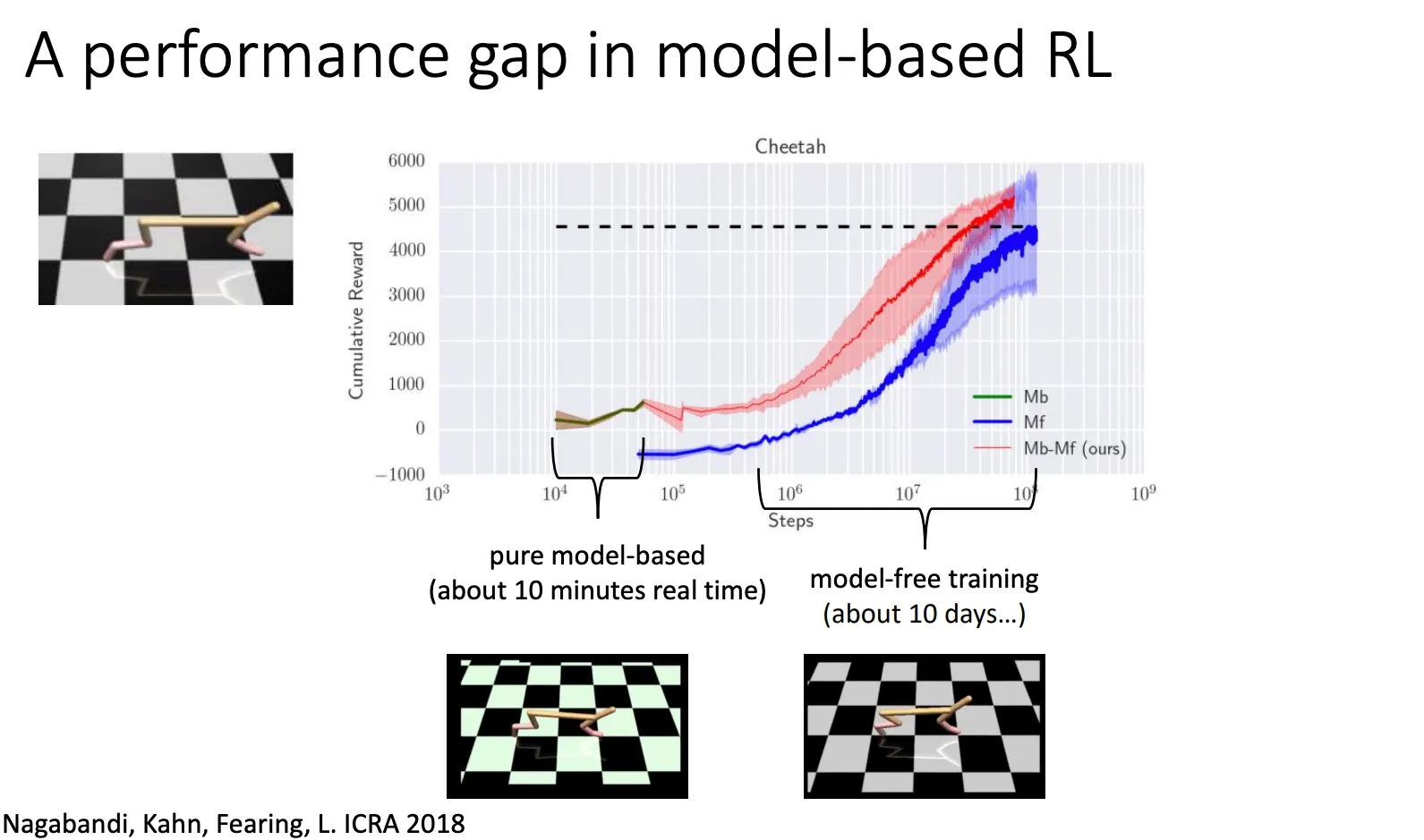
但是这种简单的 Model-Based他比不过model free的算法 alt text 当你数据不够多时（图中的黑点很少），神经网络（蓝色曲线）很容易为了强行拟合这几个点而变得扭曲（Wiggle）。

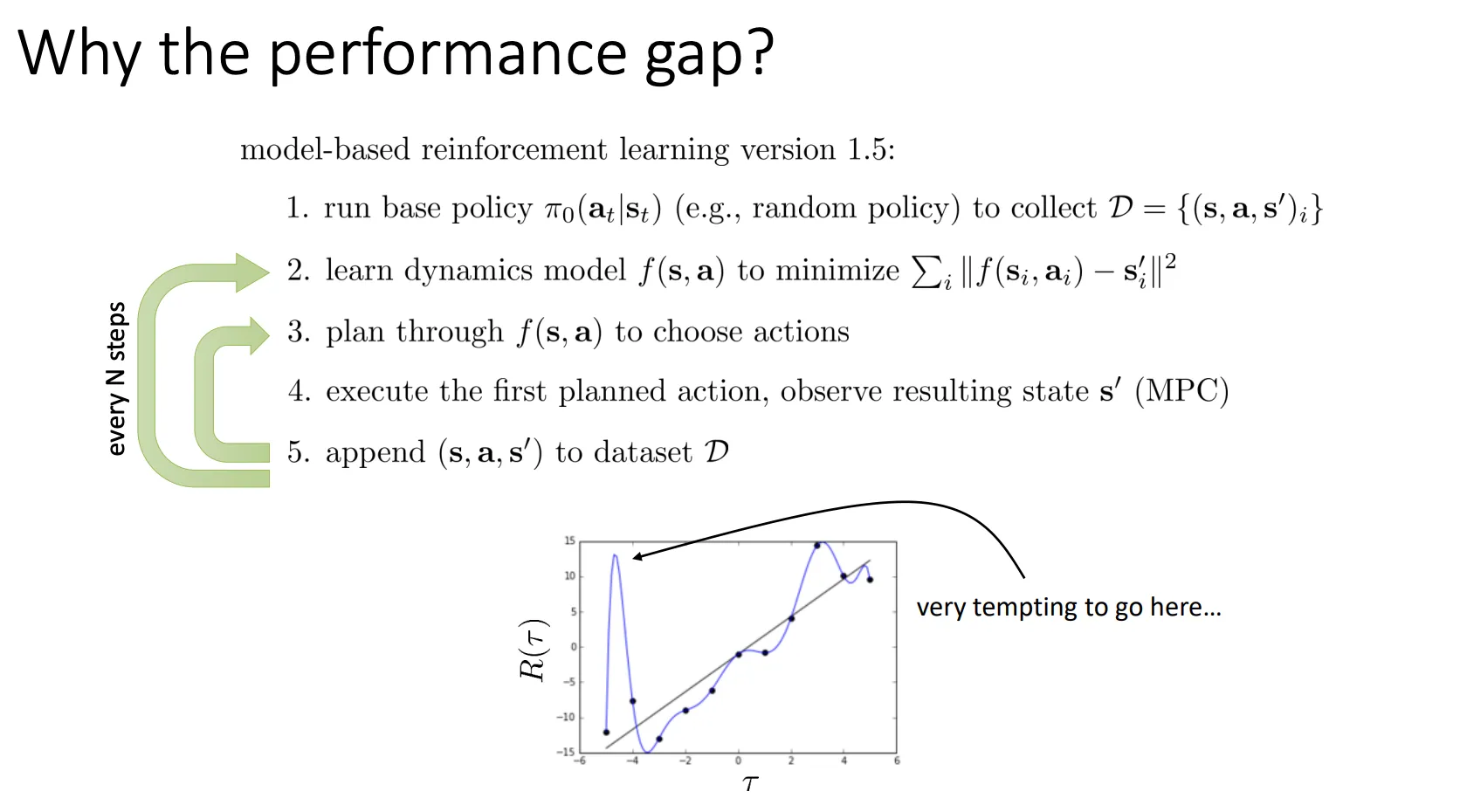
实际上那个波峰是模型“脑补”出来的幻觉（Hallucination），真实环境（直线）里那里并没有高分。这导致 Model-Based 方法在早期容易被模型的误差误导，且即使数据多了，模型也很难完美拟合复杂的真实物理世界（Model Bias）。

既然模型在未探索区域的预测不可信，那么就让模型量化自己的不确定性。于是乎我们可以在算法第三步的时候只采取那些我们在考虑了不确定性之后，依然认为期望回报很高的动作

那么怎么知道模型的不确定性有多少呢

Uncertainty-Aware Neural Net Models#

output entropy#

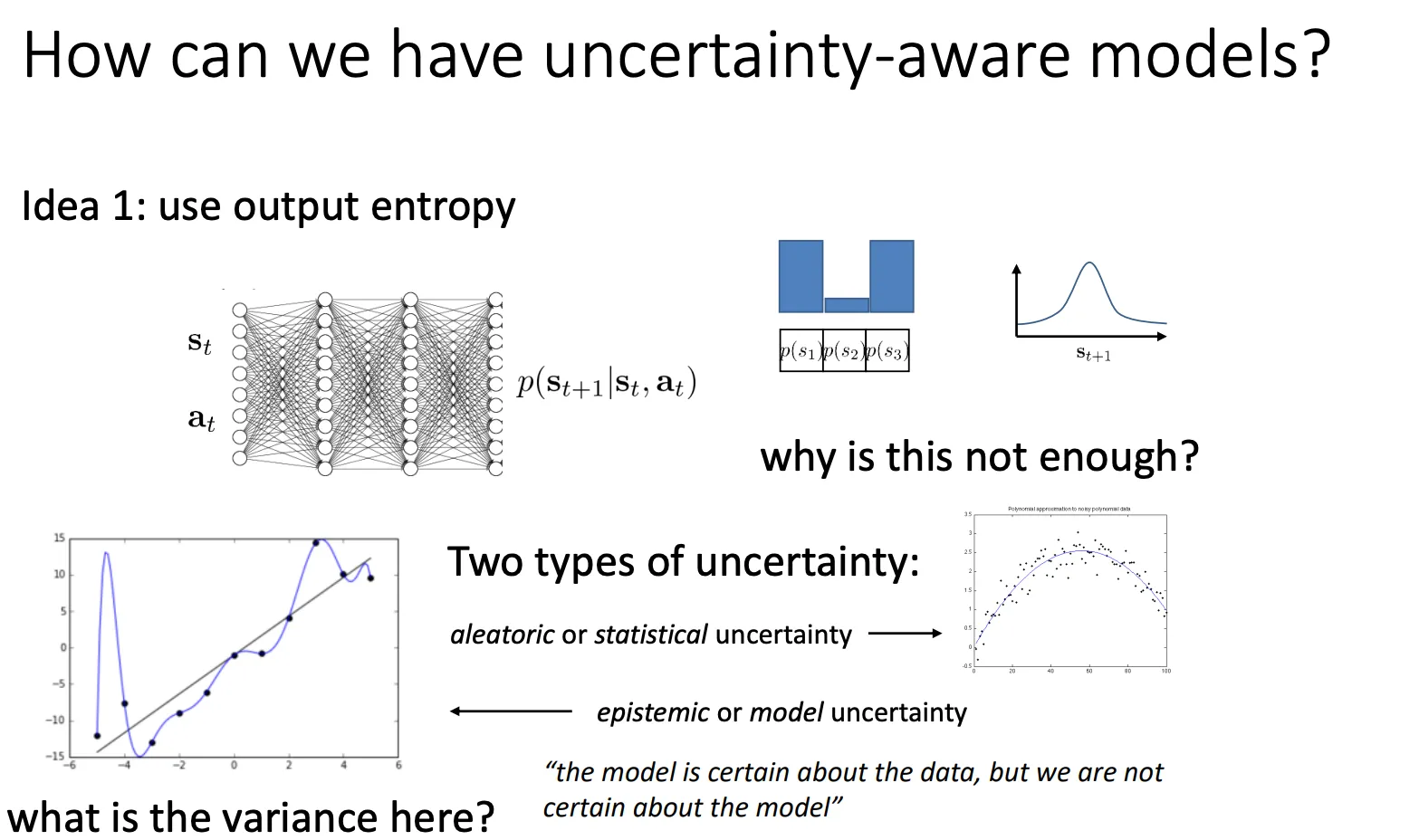
第一种就是衡量模型输出动作分布的熵是多少，但是这种方法是不好的 alt text

原因在于单纯看输出的混乱程度，你无法知道模型是因为“数据太乱了”所以不确定，还是因为“我没学过这个”所以不确定（或者甚至它在“不懂装懂”）。

它将不确定性拆解为两类：

A. 偶然不确定性 / 统计不确定性 (Aleatoric / Statistical Uncertainty)#

对应图像：PPT右下角的图。数据点本来就带有噪声，围绕着真实函数上下波动。
含义：这是数据内在的随机性（Data noise）。
- 例如：你扔一枚硬币，结果是不确定的。这是物理性质决定的，无论你的模型多么完美，你都无法消除这种不确定性。
- 关键点：增加更多的数据无法减少这种不确定性。

B. 认知不确定性 / 模型不确定性 (Epistemic / Model Uncertainty)#

对应图像：PPT左下角的图。蓝色的线（模型）为了穿过几个稀疏的黑点（数据），扭曲成了奇怪的形状（过拟合）。
含义：这是由于缺乏知识（Lack of knowledge）导致的不确定性。
- 模型可能在训练数据点上表现得很“自信”（方差小），但在没有数据覆盖的区域（Out-of-distribution），模型可能会给出完全错误的预测。
- 关键点：PPT引用的那句话 “the model is certain about the data, but we are not certain about the model”（模型对数据很确定，但我们对模型本身不确定）就是指这种情况。
- 解决方案：增加更多的数据可以减少这种不确定性。

除了这种办法不能区分这两种不确定性，他还无法捕捉“模型的无知” PPT 左下角的图（那条扭来扭去的蓝色曲线）展示了过拟合或模型本身的问题。

在这个区域，模型可能拟合出了一条非常确定的线（方差看起来很小，熵很低）。
但实际上，如果我们换一组训练数据，或者稍微改变一下模型参数，这条线可能会剧烈变化。
输出熵只能告诉你这条线目前的预测值是多少，它不能告诉你“如果我们重新训练一次，这条线会有多大的变化”。
真正的认知不确定性（Epistemic）应该衡量的是：“我对这个模型参数/这条曲线的形状有多大把握？”而不仅仅是 “这个点的预测值概率是多少？”

Bayesian neural networks#

为了解决这些问题，可以用贝叶斯神经网络。

传统深度学习）：
- 公式： $\arg\max_{\theta} \log p(\theta|\mathcal{D})$
- 解释：我们在训练神经网络时，目的是找到一组“最好的”参数 $\theta$ （即权重大模型），让它最能解释训练数据。这被称为点估计（Point Estimation）。
- 缺点：不管是通过MLE（最大似然）还是MAP（最大后验），我们最终只得到了一个模型。如果这个模型“过度自信”但其实是错的，我们无从知晓。
现在的想法：
- 公式：estimate $p(\theta|\mathcal{D})$
- 解释：我们不再寻找某一组特定的参数，而是试图去估计参数的分布。也就是说，我们想知道：在给定数据 $\mathcal{D}$ 的情况下，参数 $\theta$ 可能是哪些值？这些值的概率是多少？
- 关键点：PPT箭头指出 “the entropy of this tells us the model uncertainty!”。如果 $p(\theta|\mathcal{D})$ 这个分布很宽（熵很大），说明有很多种参数配置都能解释数据，这就意味着我们对模型到底长什么样很不确定（即模型不确定性高）。

\int p(s_{t+1}|s_t, a_t, \theta)p(\theta|\mathcal{D})d\theta

我们让所有可能的参数配置（即无数个模型）都来进行预测，然后根据它们在后验分布 $p(\theta|\mathcal{D})$ 中的概率（即该组参数靠谱的程度）进行加权平均。
结果：
- 在数据充足的地方，所有模型预测都差不多，结果很确定。
- 在数据稀疏的地方（OOD），不同的模型参数会给出天差地别的预测，平均下来的结果就会表现出很高的不确定性（如右下角图表中阴影变宽的部分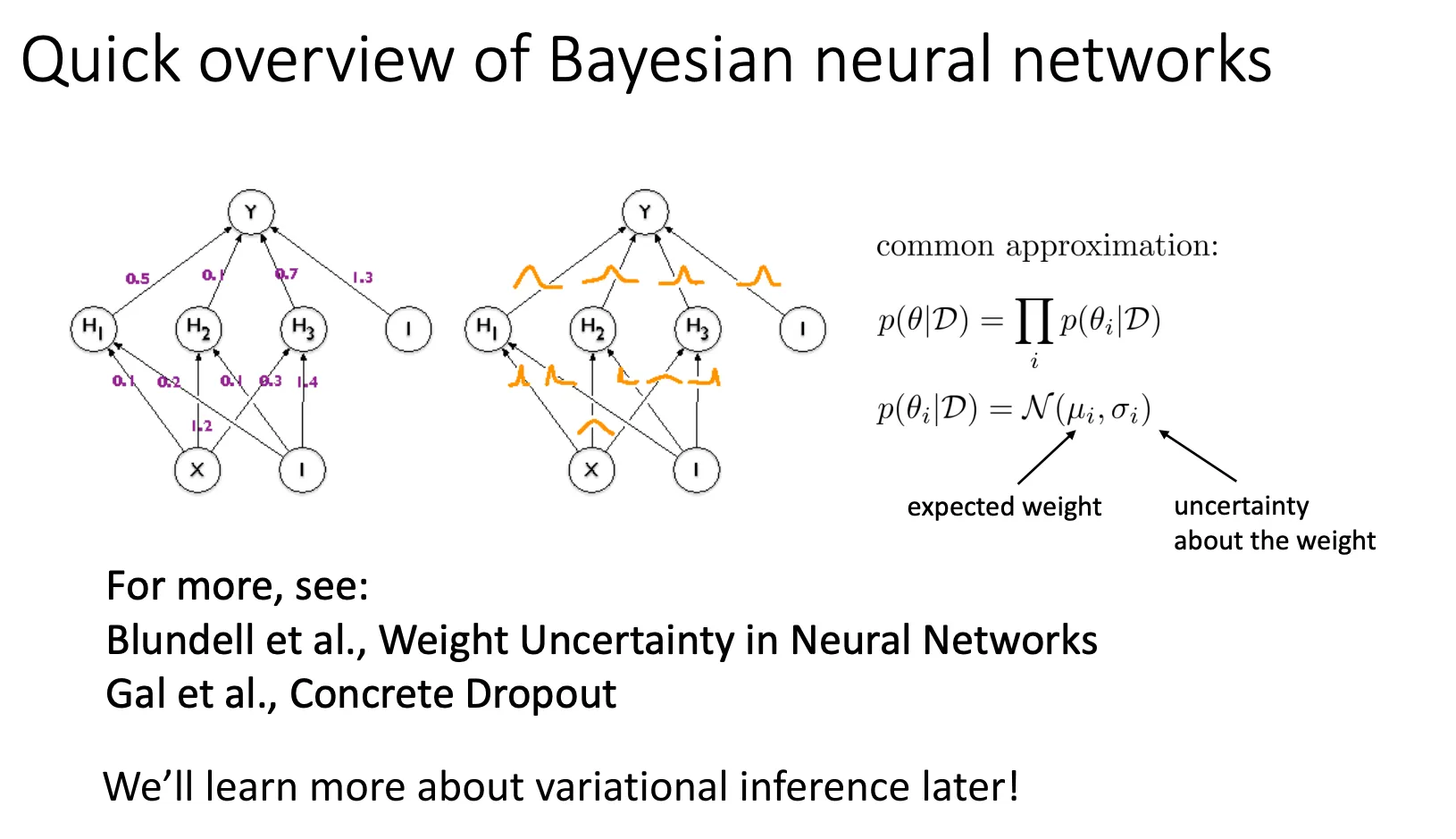）。 贝叶斯神经网络（Bayesian NN）
连接线上不再是数字，而是高斯分布。
含义：每个权重不再是一个数，而是一个随机变量（Random Variable）**。
参数变化：对于每一个连接，我们不再只学一个 $w$ $w$ ，而是要学两个参数：
- $\mu_i$ (均值/Expected weight)：权重最可能的值是多少（比如 0.5）。
- $\sigma_i$ (方差/Uncertainty)：我们对这个权重有多不确定（比如 $\pm 0.1$ ）。
计算完整的联合后验分布 $p(\theta|\mathcal{D})$ 是几乎不可能的，因为参数 $\theta$ 可能有几百万个，它们之间可能还有复杂的依赖关系。
简化的方案（Mean Field Approximation）：公式： $p(\theta|\mathcal{D}) = \prod_i p(\theta_i|\mathcal{D})$ $p (θ ∣ D) = \prod_{i} p (θ_{i} ∣ D)$
- 假设：我们强制假设网络里的每一个权重 $\theta_i$ 都是相互独立的。
- 这样我们就可以把一个巨大的复杂分布，拆解成无数个简单的小分布的乘积。
具体的分布形式：公式： $p(\theta_i|\mathcal{D}) = \mathcal{N}(\mu_i, \sigma_i)$ $p (θ_{i} ∣ D) = N (μ_{i}, σ_{i})$
- 我们假设每个权重都服从正态分布（高斯分布）。
- 训练目标：以前我们训练是调整 $w$ 来降低 Loss；现在我们训练是调整 $\mu$ 和 $\sigma$ ，使得这个分布能最好地拟合数据。

Bootstrap ensembles#

alt text 贝叶斯太复杂了，我们可以有一个更实用简单的方法就是训练多个相互独立的传统模型

一致（Low Variance）：如果这 $N$ 个模型对同一个输入 $(s_t, a_t)$ 给出了几乎一样的预测，说明大家都很确定，不确定性低。
分歧（High Variance）：如果有的模型说往左，有的说往右，大家意见不合，说明面对这个情况模型很迷茫，不确定性高。

数学上其实就相当于

\int p(s_{t+1}|s_t, a_t, \theta)p(\theta|\mathcal{D})d\theta\approx \frac{1}{N} \sum_i p(s_{t+1}|s_t, a_t, \theta_i)

然后怎么让模型相互独立呢，方法就是bootstrap。假设原始数据集 $\mathcal{D}$ 大小是N，然后我可以重复抽N次就构成 $\mathcal{D}_i$ 数据集，拿这个数据集训练一个模型。最终这些模型就是相互独立的

我们可以用这个不确定性来规划我们的动作 alt text

Model-Based RL with Images#

alt text 当机器人或 Agent 只能看到图像（observation, $\mathbf{o}$ ），而无法直接获得真实的物理状态（state, $\mathbf{s}$ ）时，如何构建一个数学模型来描述世界的运作规律，并用于训练。

我们很难说在图像像素层面预测未来，因为

High dimensionality（高维性）：一张图片包含成千上万个像素，直接预测下一帧的每一个像素计算量巨大且极难收敛。
Redundancy（冗余性）：图片里有很多无关信息（比如机械臂背景里的墙、桌子的纹理），这些对任务并不重要，但占用了大量数据。
Partial observability（部分可观测性）：单张静态图片可能无法包含所有信息（比如物体的速度、被遮挡的物体），这使得 $s_t$ 实际上变成了 $o_t$ （观测），而非完整的系统状态。

于是乎我们想要将这个问题解耦

$p(o_t|s_t)$ (Observation Model / Encoder-Decoder)：负责处理“高维但非动态”的部分。即学习如何把复杂的图像压缩成简单的状态 $s$ （或者从 $s$ 还原图像）。这解决了高维和冗余问题。
$p(s_{t+1}|s_t, a_t)$ (Dynamics Model / Transition)：负责处理“低维但动态”的部分。即在压缩后的低维空间里预测未来。因为维度低，预测变得容易且高效。

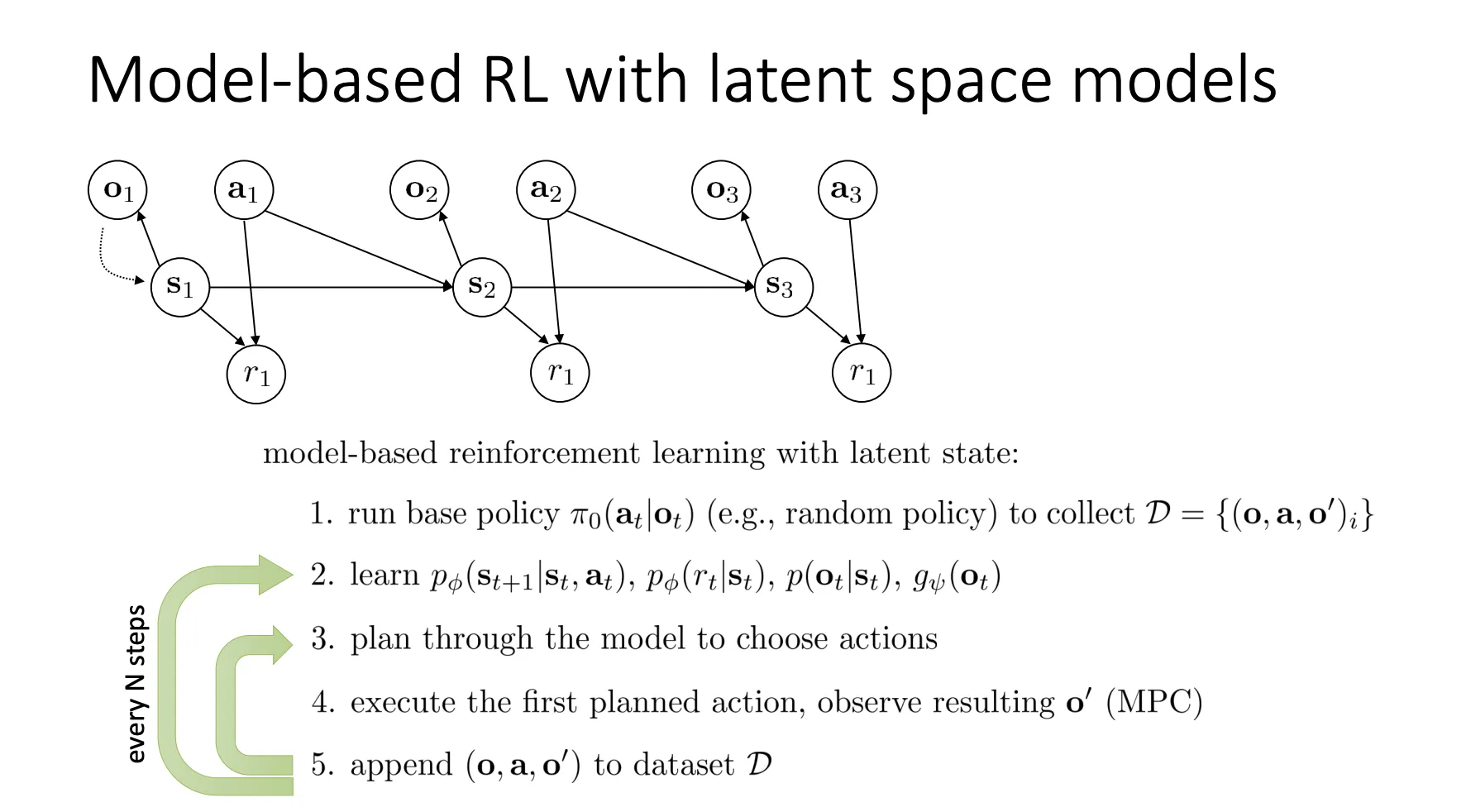
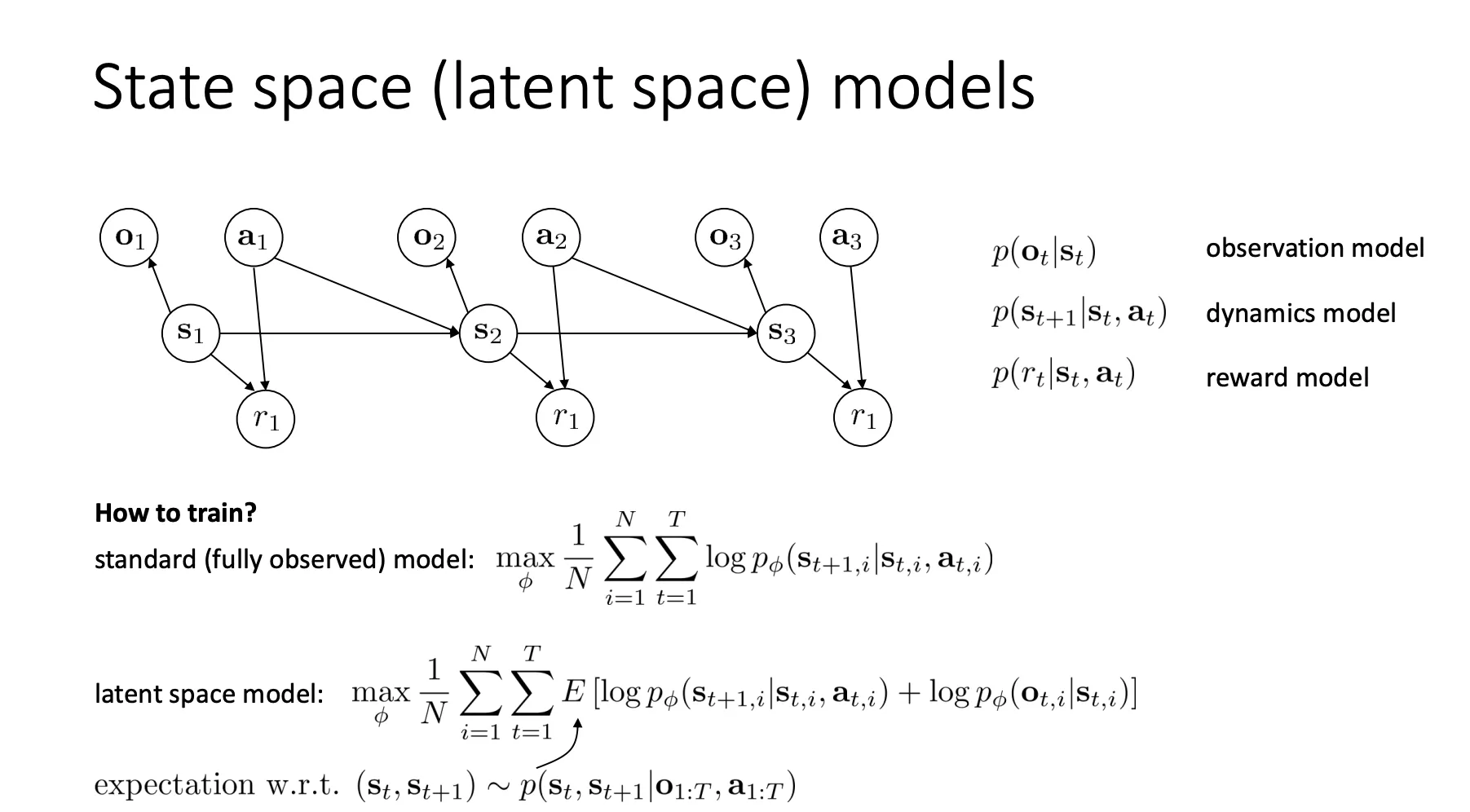alt text 这张图展示了问题的核心结构，即一个 POMDP（部分可观测马尔可夫决策过程） 的图模型。

图模型结构 (PGM):
- $\mathbf{s}_t$ (Latent State): 这是一个不可见的“潜在状态”（比如机器人的关节角度、物体的真实物理位置）。
- $\mathbf{o}_t$ (Observation): 这是 Agent 实际看到的（比如摄像头拍到的像素图片）。 $\mathbf{o}_t$ 由 $\mathbf{s}_t$ 生成（Observation model）。
- $\mathbf{a}_t$ (Action): 动作。
- $\mathbf{s}_{t+1}$ (Dynamics): 下一时刻的状态取决于当前状态和动作。这是我们需要学习的核心“动力学模型”。
训练目标 (How to train?):
- 标准模型 (Standard): 如果我们知道真实状态 $\mathbf{s}$ ，直接最大化 $p(\mathbf{s}_{t+1}|\mathbf{s}_t, \mathbf{a}_t)$ 的对数似然即可（类似监督学习）。
- 潜在空间模型 (Latent space model): 因为 $\mathbf{s}$ 是未知的，我们无法直接训练。因此，目标变成了最大化观测数据 $\mathbf{o}$ 的似然概率。
- 公式中的 $E[\dots]$ 表示我们需要针对潜在状态分布求期望。这实际上是在通过 变分推断（Variational Inference） 的思路，最大化 ELBO（Evidence Lower Bound）。由于现在我们不知道s是多少，于是我们可以根据o去预测s，我们就训练一个神经网络（Encoder， $q$ ）来近似它。

选项 A: Full smoothing posterior ( $q(s|o_{1:T}, a_{1:T})$ )
- 做法：利用所有的历史数据（甚至未来的数据，如果是离线训练）来推测当前的 $s_t$ 。
- 优缺点：最准（Most accurate），因为信息量最大，但计算最复杂（Most complicated），通常需要用到 RNN 或 Transformer。
选项 B (红圈): Single-step encoder ( $q_{\psi}(s_t|o_t)$ )
- 做法：只看当前这一张图 $o_t$ ，直接推测 $s_t$ 。
- 优缺点：
  - Simplest（最简单）：这就是标准的 VAE Encoder，给一张图，出一个向量。
  - Least accurate（最不准）：因为它丢失了时序信息（比如无法通过一张静态图判断物体的速度/加速度）。

我们目前先看最简单的Single-step encoder，而且是deterministic的情况 alt text 我们就可以用o来估计s。公式上就用encoder和o来代替s。

把奖励加上，我们就可以更新我们想要的训练公式 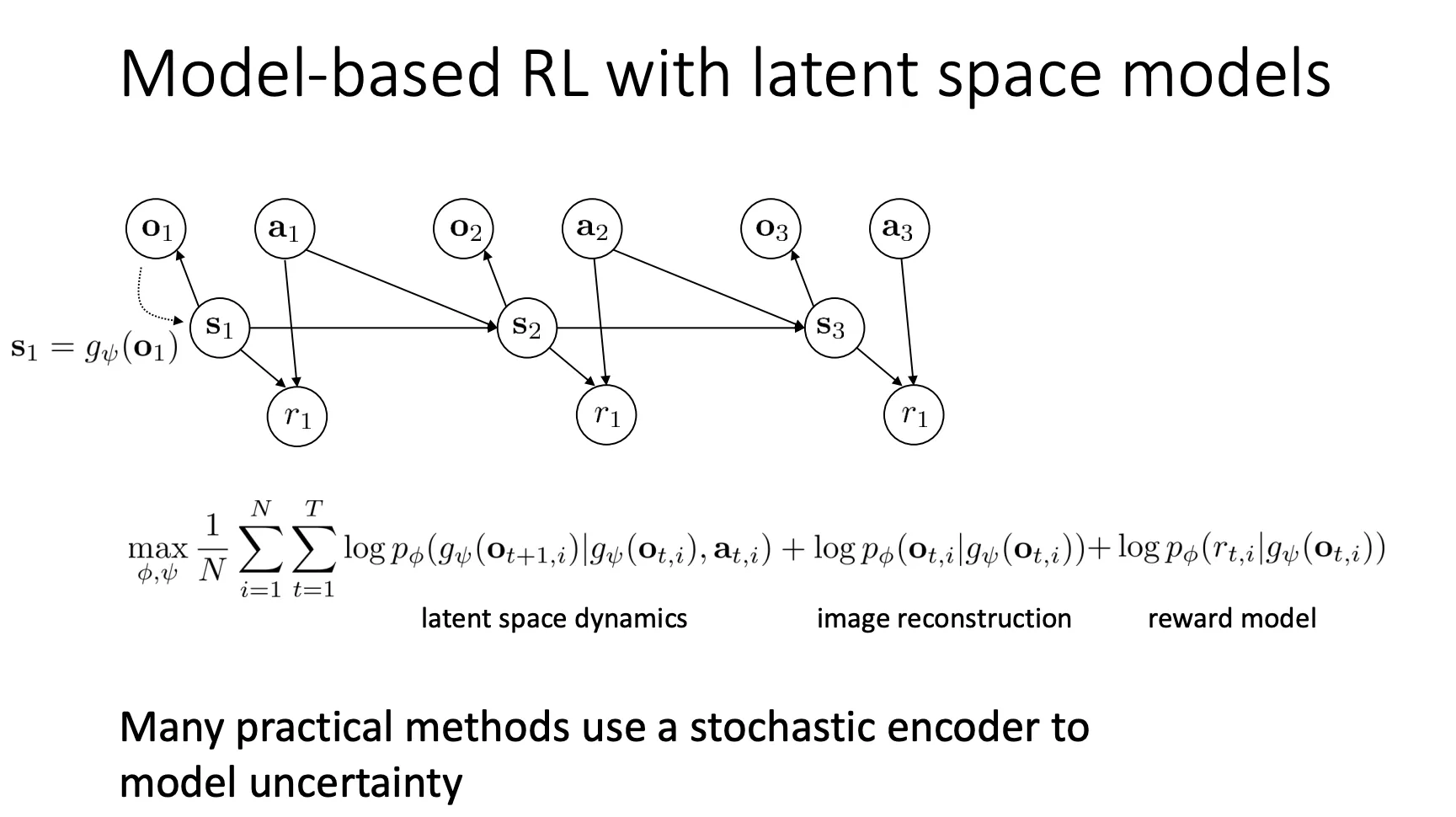alt text 最终套用一下原本的训练框架，就得到了对应的训练流程