Lecture12 Recurrent Networks

前言#

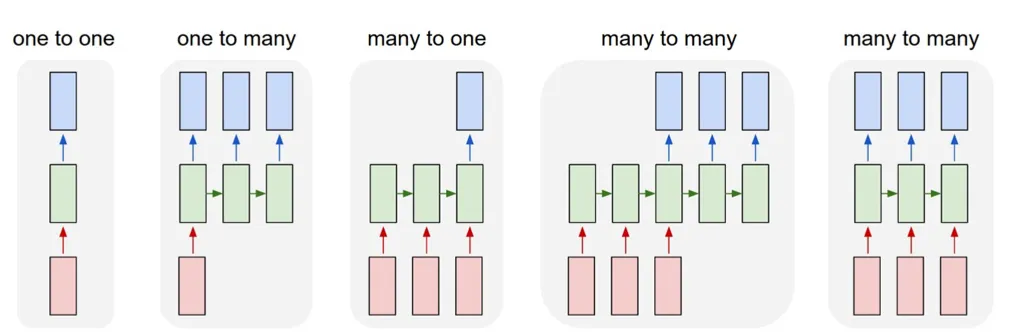
之前我们讲的一直都是图像识别，也就是单图片单输出，但是我们还想用deeplearning来做些更多的事情，比如

• one to many 输入一张图片，然后输出一系列描述这个图片的语言
• many to one 输入一系列图片，然后识别。比如视频的识别
• many to many 比如翻译，以及每一帧的识别

RNN#

他的想法就是我们根据当前时间段的输入$x_t$和前一段时间的状态$h_{t-1}$来决定当前时间段的输出$h_t$，然后我们就要学两个参数$W_{hh},W_{xh}$ 。 $tanh(x)=\frac{e^x+e^{−x}}{e^x−e^{−x}}​$双曲正切是一个激活函数

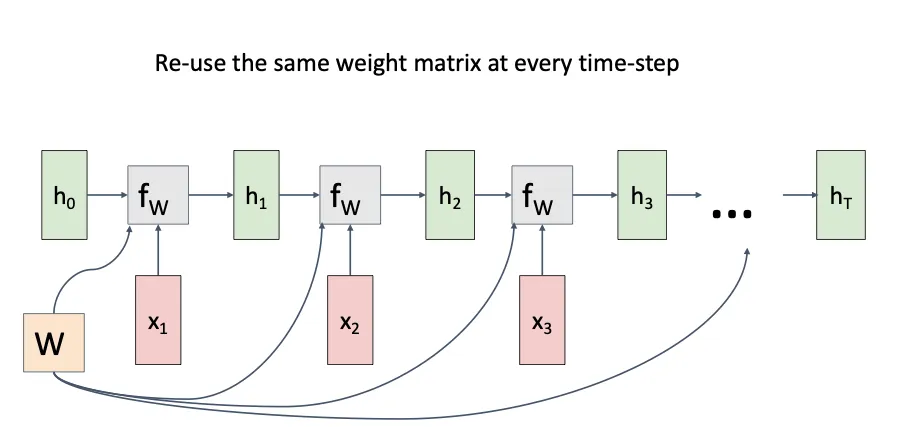所以他的流程就类似这种，值得注意的是，他的W对于每一个状态而言都是固定的且共享的。但是从直觉上来看，如果我对每一次的输入和状态都有一个特定的W的话，我的模型的能力不应该会更强吗。GPT解释道RNN的本质是要对任意长度的序列进行统一建模，如果我的每一个时间步都有一个独立的权重，那我似乎只能处理固定长度的输入；其二是训练参数的减少；其三是RNN更像是循环执行一个神经单元，就想人处理语言时，面对不同位置的词，其处理机制是类似的，只是记忆（上下文）不同。

但这些吧，感觉似乎都可以被解决，anyway～

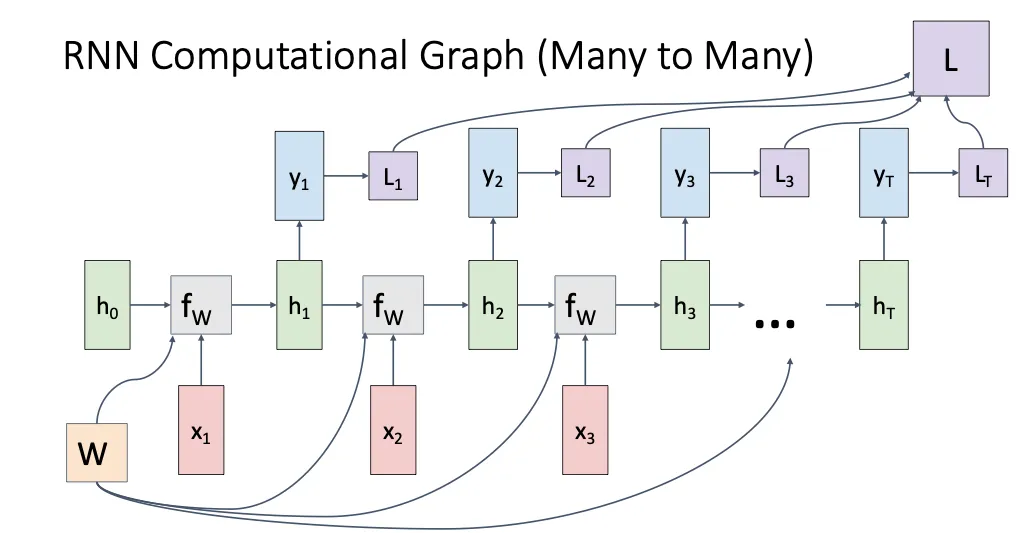
Many to Many#

我们在每个时间步都输入数据，然后每个时间步输出，同时他又对应的损失函数，将每一个时间步的损失函数汇总在一起就可以得到总的损失函数

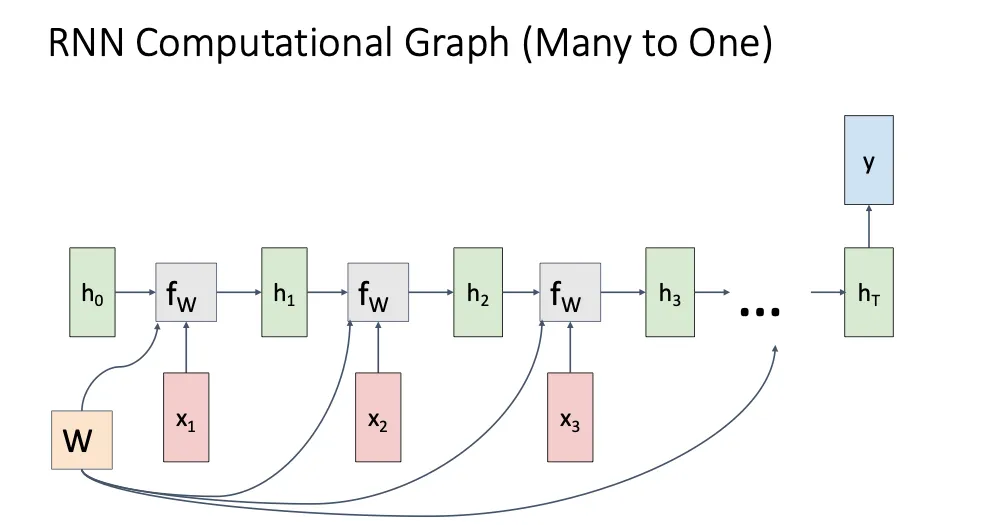
Many to One#

我们只在最后一个时间步给出一个输出，比如用来做视频的分类

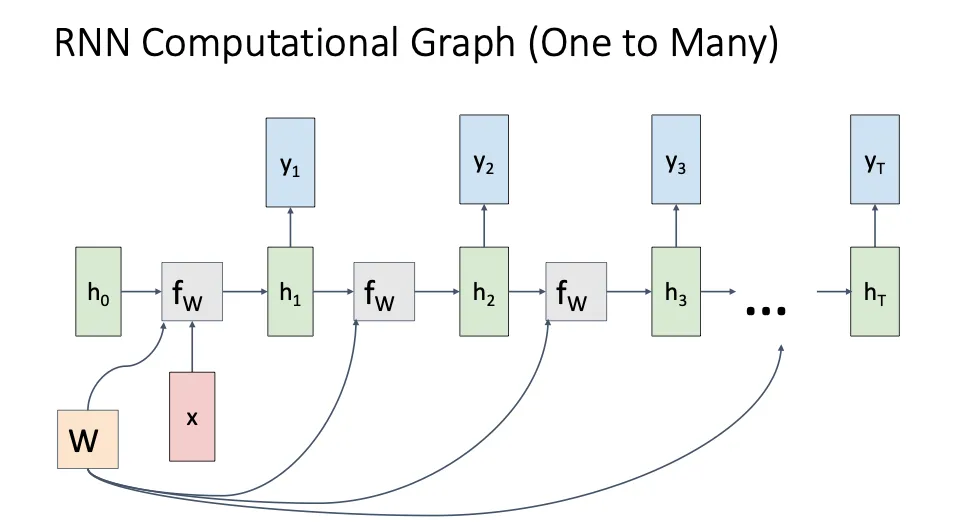
One to Many#

我们只在一开始给输入，然后后面就没有

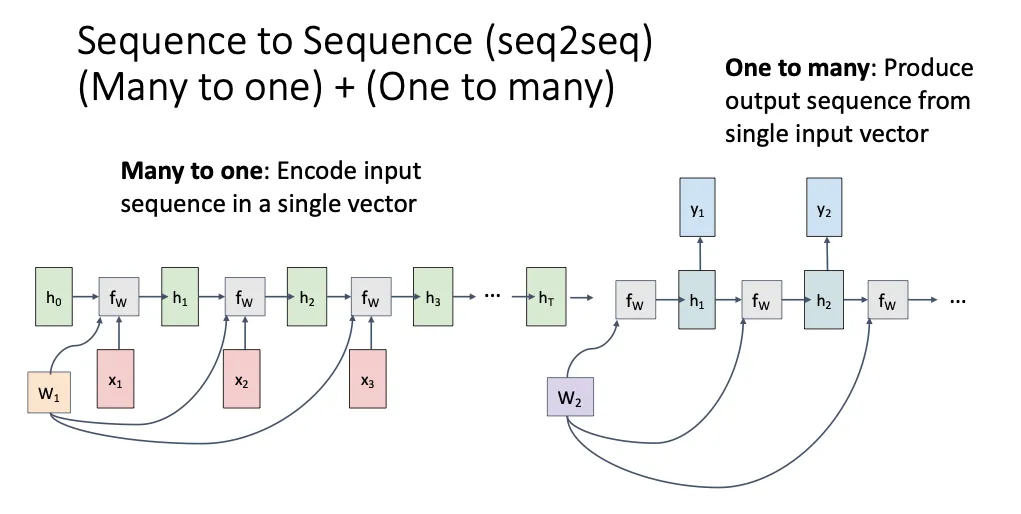
Sequence to Sequence#

上面提到的多对多一般是输出和输入的长度是一样的，但是有的时候我们想要的输入输出的长度可能不一样。比如翻译，两个不同的语言描述同一个事情所用的tokens可能是不同的，所以为了解决这个问题，就有Many to One + One to Many这两个模型拼接在一起，我们将一开始的输入输入到Many to One模型中，将最后得到的输出输入到One to Many的模型中，前面一个叫encoder，后面一个叫decoder。注意这里我们用两套不同的权重。 但是这就引出一个问题，第二个模型怎么控制输出的长度呢？

Language Modeling#

这里以大模型举例子我觉得还是很好理解的，每次预测的输出当作下一次的输入，这样你就可以无限的输出

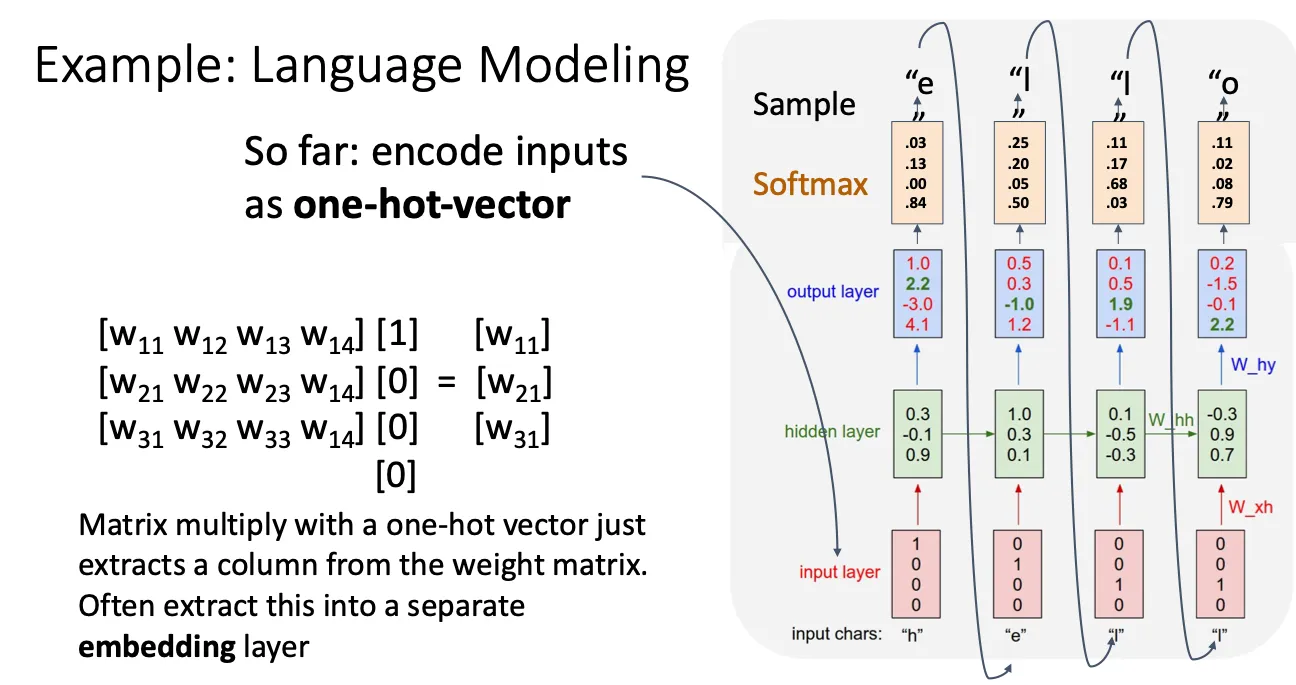
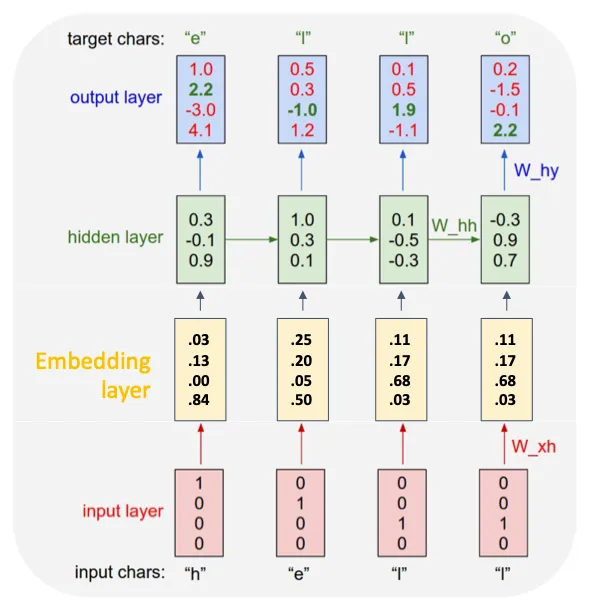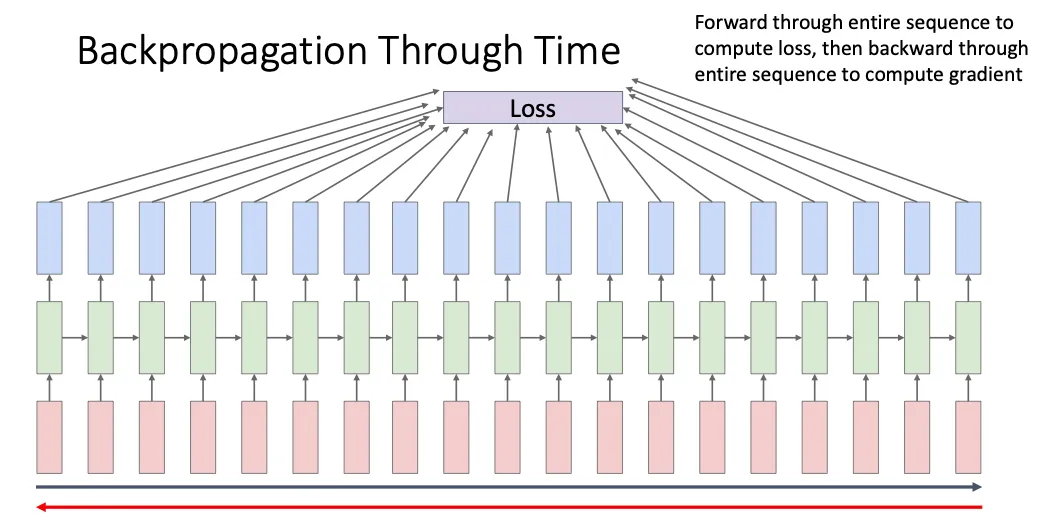
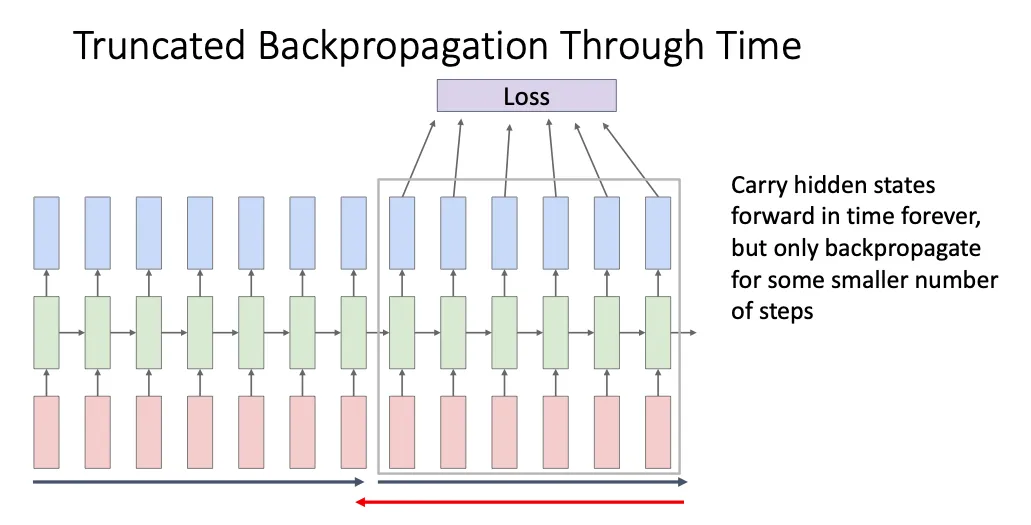
这一部分主要讲的就是一开始我们用one hot作为输入，但是这个很明显这里面包含的信息太少且太稀疏了，所以就用一个embedding layer。这个本质就是一个矩阵，one hot乘了这个矩阵本质就是提取这个矩阵中对应的一列，他和one hot同样可以表示相同的值，但是他的维数会更低，信息会更密集，更主要的是这个layer是可以学习的，他可以学习词与词之间的关系，从而调整矩阵的权重，这样他里面的一列他就可以包含更多的信息。 那么他是怎么更新权重的呢？ 首先自然而然的就是把所有时间步的损失加起来，然后最后反向传播更新权重，但是这样的做法有一个很大的弊端就是他太占用内存的空间了，没有那么多显存。 于是就有下一个方法 我们将这个序列分成一小块一小块的，每次计算完一小块的loss我们就更新他的权重，这样确实节省了很多内存，但是这时候就有一个问题就是他很难学习到很远的内容之间的联系，直观上看，他只是根据一小块里面的内容来更新权重，所以他学习到的权重应该只是那一小块的。

Visual Modeling#

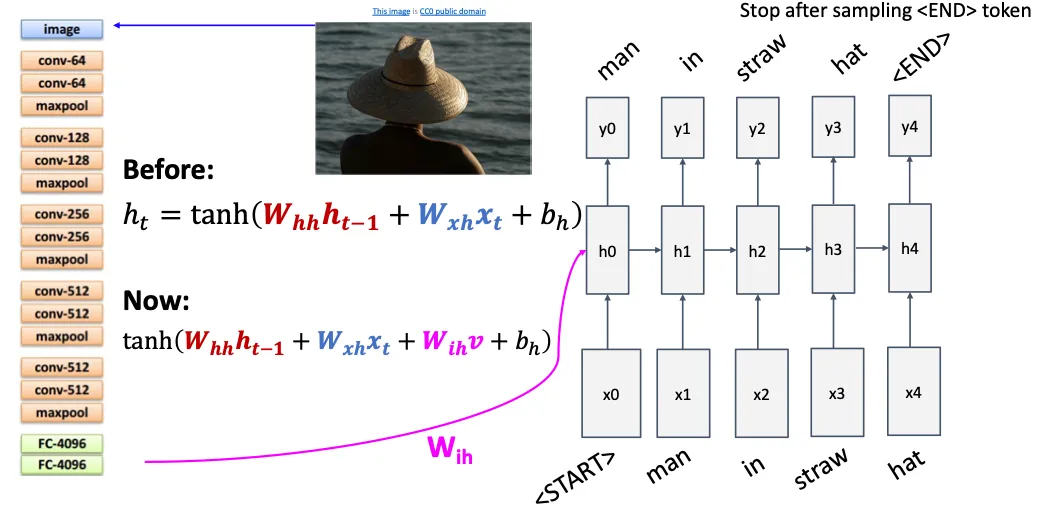
回到视觉上面的话，这里我们考虑的是一对多的场景，给一幅图片然后生成描述文字，我们先用CNN提取出图像特征，然后将这个特征输入到RNN中，他的函数就多加一个$W_{ih}v$ 。

然后值得一提的就是我们一开始输入了<START>然后最后输出<END>,当模型输出<END>的时候我们就终止继续生成。由此解决之前的问题。

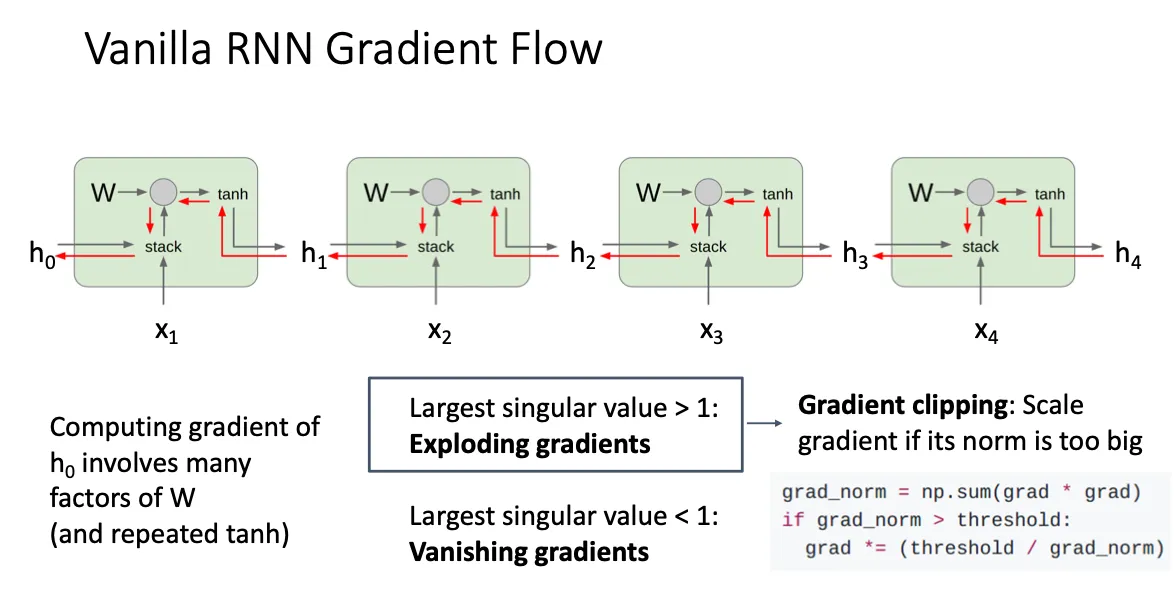
Vanilla RNN Gradient Flow#

我们之前讲的属于Vanilla RNN模型，然后他的梯度计算就像是图中所示 仔细推导一下他的反向传播，假设我们现在有3个时间步

$$\begin{array}{r} h_1 = \tanh(W * h_0 + U * X_1) \\ h_2 = \tanh(W * h_1 + U * X_2) \\ h_3 = \tanh(W * h_2 + U * X_3) \end{array}$$

整合一下就是

$$h_3=\tanh(W\cdot\tanh(W\cdot\tanh(Wh_0+Ux_1)+Ux_2)+Ux_3)$$

然后令

$$\begin{aligned} & & & a_1=Wh_0+Ux_1 \\ & & & h_1=\tanh(a_1) \\ & & & a_2=Wh_1+Ux_2 \\ & & & h_2=\tanh(a_2) \\ & & & a_3=Wh_2+Ux_3 \\ & & & h_3=\tanh(a_3) \end{aligned}$$

那么对W的梯度就应该是

$$\frac{\partial h_3}{\partial W}=\frac{\partial h_3}{\partial a_3}\cdot\left(\frac{\partial a_3}{\partial W}+\frac{\partial a_3}{\partial h_2}\cdot\frac{\partial h_2}{\partial a_2}\cdot\left(\frac{\partial a_2}{\partial W}+\frac{\partial a_2}{\partial h_1}\cdot\frac{\partial h_1}{\partial a_1}\cdot\frac{\partial a_1}{\partial W}\right)\right)$$

初步计算一下转化为

$$$$

注意到这个是式子中相当于有很多的W连乘，然后对于一个矩阵W，我们可以对他进行奇异值分解

$$W = U * Σ * V^T$$

其中U,V属于旋转矩阵，Σ是个对角矩阵，他里面的值就是奇异值，他就会对向量进行伸缩，当我们对W进行不断的连乘的时候如果他的奇异值大于1，那么他就会一直放大某个方向上的分量，这就会导致所谓的梯度爆炸；相反，如果奇异值小于1，那么他就会一直压缩某一方向上的分量，这就叫梯度消失。

对于RNN中的梯度爆炸问题，解决方法就是梯度裁剪（Gradient Clipping） 设一个参数的总梯度是向量 $g$，我们限制它的 2-范数（L2 范数）不超过某个阈值 $\tau$。 设有函数$f(x_1,x_2,\ldots,x_n)$,其梯度为：

$$\nabla f=\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\ldots,\frac{\partial f}{\partial x_n}\right]^\top$$

梯度向量的范数 (通常是 2-范数) 表示该梯度的“整体变化强度”:

$$\|\nabla f\|=\sqrt{\left(\frac{\partial f}{\partial x_1}\right)^2+\cdots+\left(\frac{\partial f}{\partial x_n}\right)^2}$$

如果：

$$\| g \|_2 > \tau$$

就进行缩放：

$$g \leftarrow \tau \cdot \frac{g}{\| g \|_2}$$

也就是按比例缩小它，使总长不超过 $\tau$。

那么对于梯度消失而言呢，为什么不采用同等的方式对梯度进行放大呢，感觉这个就有点经验性了，有的解释就是他的梯度变得越来越小，也就是他里面有用的信息越来越少，如果我们对他放大，很有可能放大的就是噪声。而经验告诉更好的做法反倒是重新改进结构。

Long Short Term Memory (LSTM)#

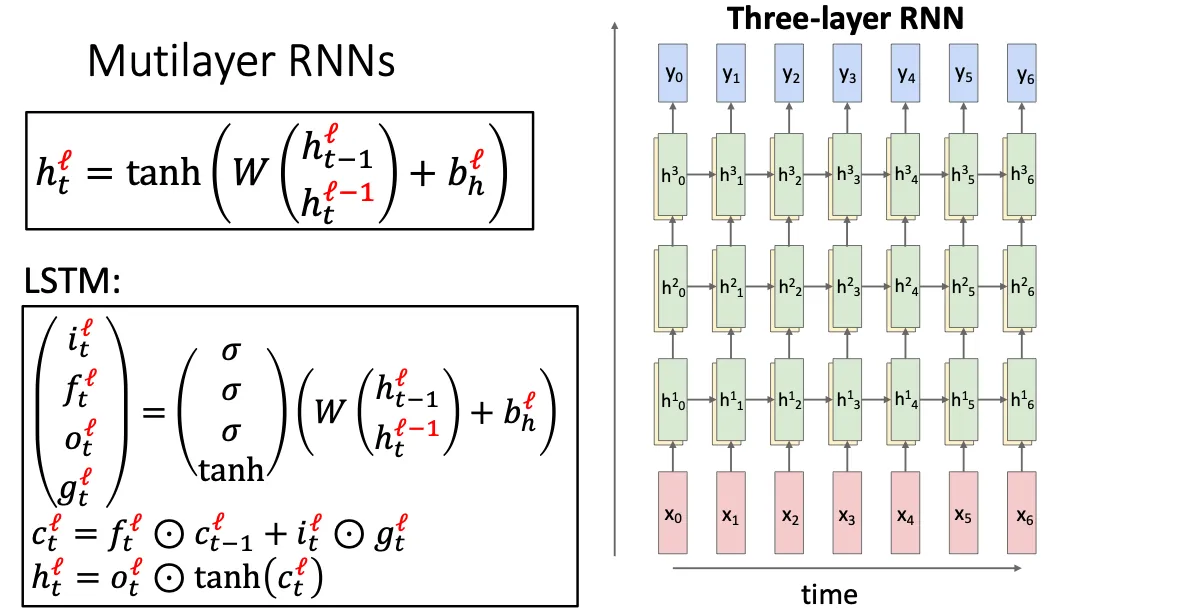
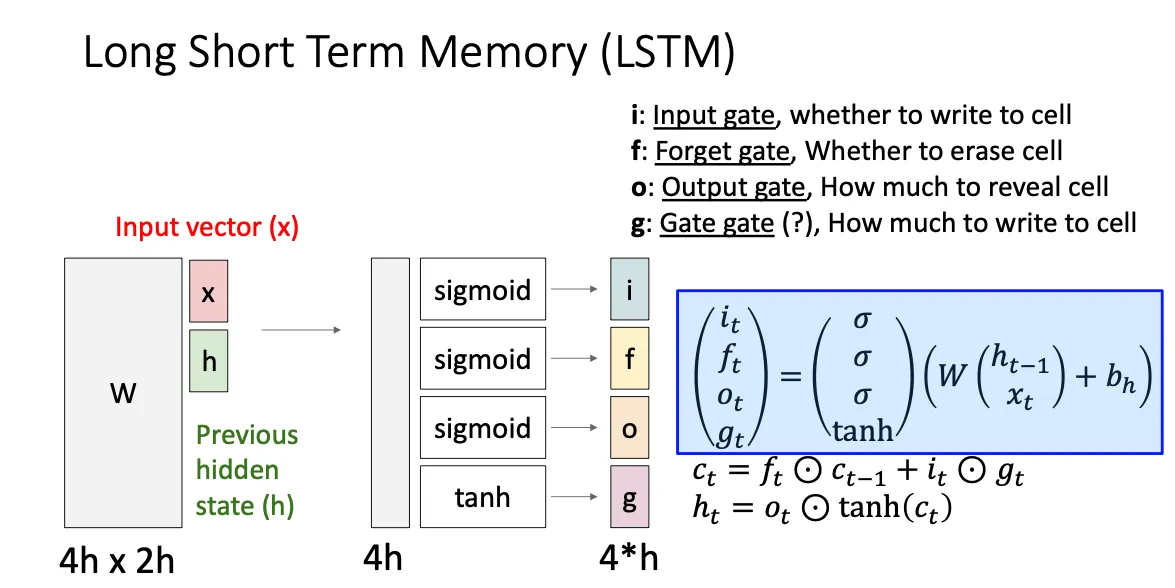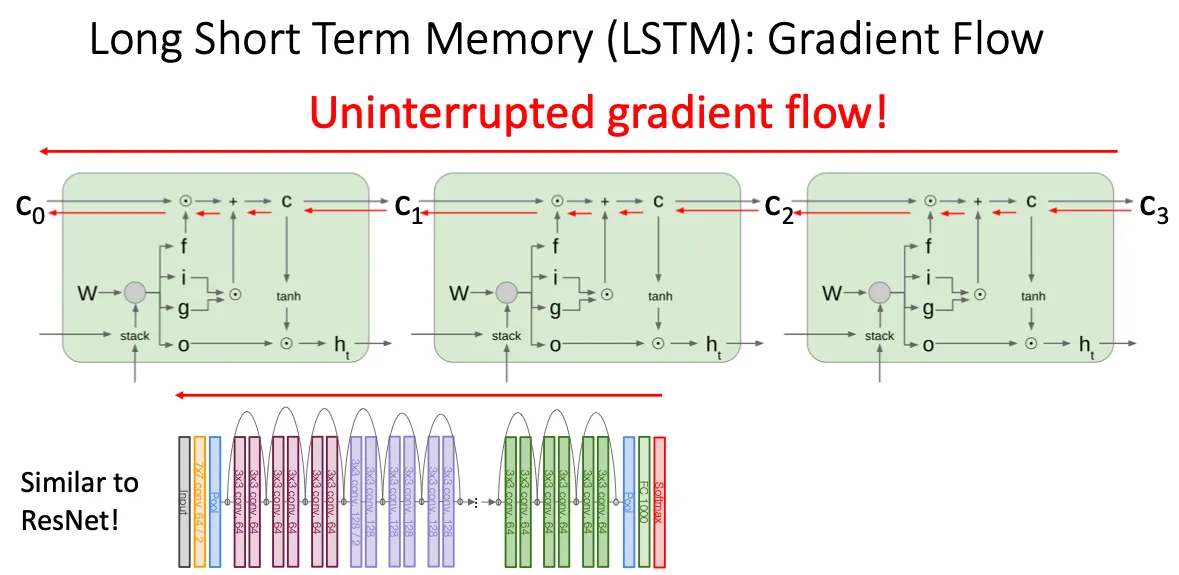
为了解决梯度消失的问题，人们就想出LSTM，这想法感觉很神奇。他引入了一个c，叫做cell state，主要思想就是将h和x结合起来和W相乘之后，将每一列取出来分别作为gate，然后执行不同的运算 如下图所示，大概就是这样，然后他的解释就是上图那些gate的定义，感觉就很tricky 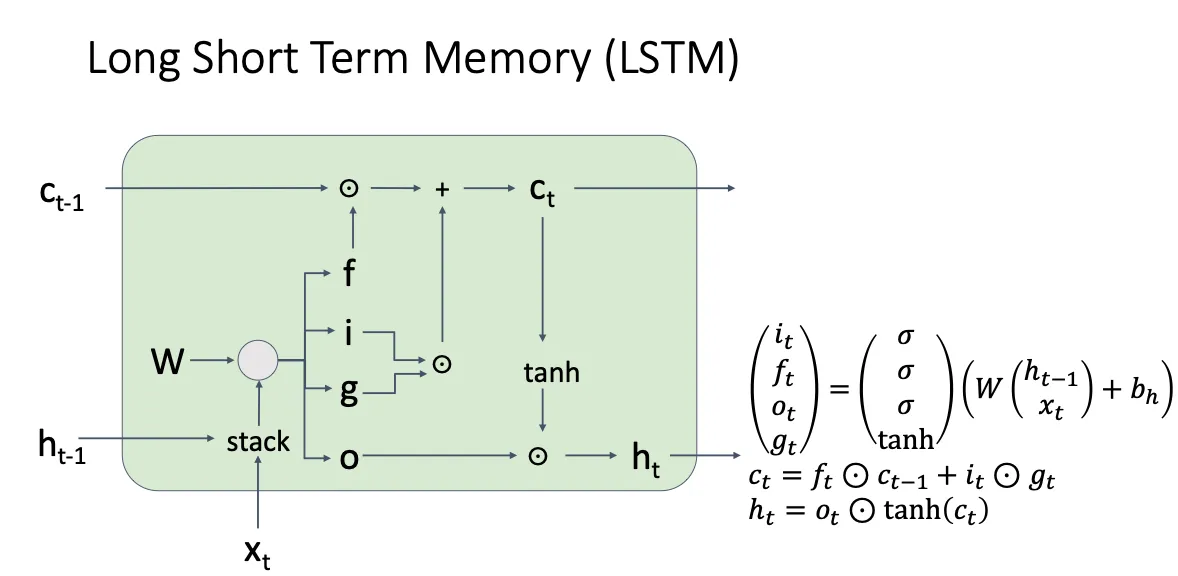所以他到底是怎么解决梯度消失的呢，主要思想就是对于C而言，这条通路上的梯度几乎没有什么损失，虽然说我们在对W进行梯度更新的时候还是会有激活函数，矩阵乘法这种求导会有损失，但他的思想就是他保留了一部分，至少没有损失的一部分。从而避免像Vanilla RNN中的W的更新一直是损失的，这个思想其实和ResNet很像，就像提供了一条高速路一样。 有意思的是上课有同学提到到底是怎么想到这种结构的，答案就是research，很搞笑，就是很多人不断的试，不断的验证新的点子，总有人最终会想到一个有用的点。好听一点叫Trial and error，地狱一点叫炼丹，这时候才想起来有人曾经说过的一句话，我们需要出现deeplearning中的香农，太有感觉了。

最后的内容就是我们可以将CNN中多层的思想放到RNN中，我们将hidden state的输出直接作为下一层的输入。通常来说每一层的W是不一样的，然后一般不会像CNN一样放很多层。