学生期末考试排列启发式算法

起因#

最近期末考试压力有点小大，正好最近在复习算法，回宿舍的途中，我就在想，我既然学了这么多算法，那是不是世界中的所有问题都可以有一个算法来解决呢。正好当时想到军训的时候有同学问选课的事情，学生问了具体什么问题忘记了，但老师回答说，如果出现这种问题，可以找教工部。然后我就在想，教工部是如何给学生的期末考试进行排序的呢。

想要达到的目的一个是优先时间最短，就是怎么样安排，使得整个的期末考试持续时间最短，第二个优化的目标就是在时间最短的前提下怎么让教室安排的数量最少，意思就是我让我所需的最小教室数最小。

带着我觉得我学了算法，我就应该可以解决生活中的很多问题，于是路上我就开始思考，本博客就记录一下。

思路#

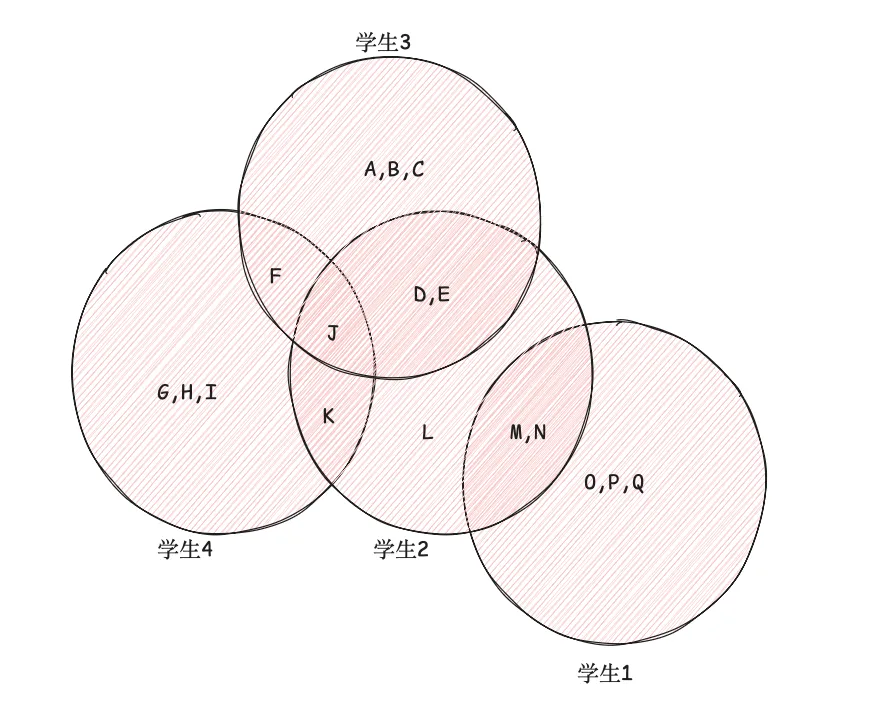
首先，我们将所有学生的选课放入一个集合中，每一个学生就有自己对应的一个集合。然后这些集合之间就有交集，然后我们就把所有学生的集合放到一起，组成一个复杂的图案。 如图就是就假设学生1这学期修的课程是O,P,Q,M,N，然后以此类推。那么我们可以根据这个有一些发现

1. 同一个圆圈(集合)内的课程不能被安排在同一个时间段，这是一种冲突
2. 两个集合除了交集之外可以并行考试
3. 交集表示学生共同上的课程，给其中一个学生安排交集中的课程，就要同时给所在这个交集中的其他学生也安排上这个课程

ok，那么我的思路就是把图中没有包含在任何交集中的课程拿出来，然后对于在同一个集合中的这些课程我们看作是一组。比如图中，O-P-Q是一组，G-H-I是一组以此类推，然后我把这一组叫做一条并行链，每一列表示一个时间段。那么我们可以画出4条并行链：

链1	A	B	C
链2	O	P	Q
链3	G	H	I
链4	L

随后，剩下的课程都是在集合中的交集部分，随后我们依次遍历所有集合中的交集部分的元素，然后添加进表中，比如对于链1而言，我们依次添加进F,J,D,E 同时也把该课程添加进该课程所在的别的链中。此时注意，如果我们在添加课程到别的链中的时候，发生冲突，则向后找合适时间段，找到第一个合适的时间段就放入。

链1	A	B	C	F	J	D	E
链2	O	P	Q
链3	G	H	I	F	J
链4	L				J	D	E

然后以此类推到链二

链1	A	B	C	F	J	D	E
链2	O	P	Q	M				N
链3	G	H	I	F	J
链4	L			M	J	D	E	N

链三

链1	A	B	C	F	J	D	E
链2	O	P	Q	M				N
链3	G	H	I	F	J				K
链4	L			M	J	D	E	N	K

链四没有变化

于是乎我们就得到了一个没有冲突的安排表，并且一定程度上的并行了一些课程。

当想到这一步的时候，我觉得我应该找到最优解，但是当我把这个问题问GPT的时候，他跟我说这是一个NP=P的问题，意思就是目前为止我们没办法得出一个不是O(n!)方法来找到最优解。

确实如此，本质上来说，我的做法就是贪心，局部最优不一定全局最优，比如图中我可以这样安排

链1	A	B	C	F	J	D	E
链2	O	P	N	M	Q
链3	K	H	I	F	J	G
链4	K	L	N	M	J	D	E

这是一个全局最优解，因为总的期末考试时间>=最大学生的选课数 ，所以至少需要安排7场考试才能满足所有学生。

问题到这里，还没有结束，原本我以为我的贪心做法是最优的时候，我就继续去找安排课室数量的最优，但很可惜，在有限的时间内我想过将表中的点连起来，有共同的就用一根线连起来，在一条并行链中的也用线连起来，空的就用一个空符号连一起，这样就变成一个图的问题。类似这种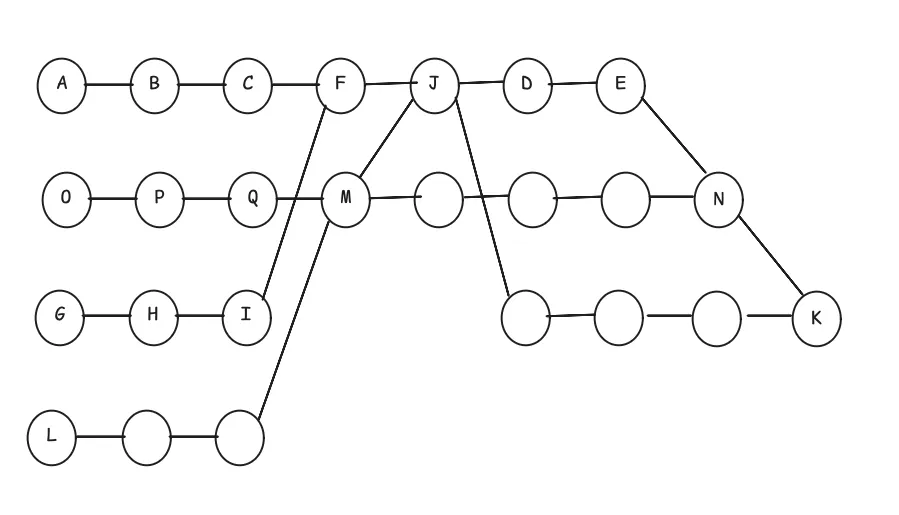： 或者这种，类似华容道一样排列这些 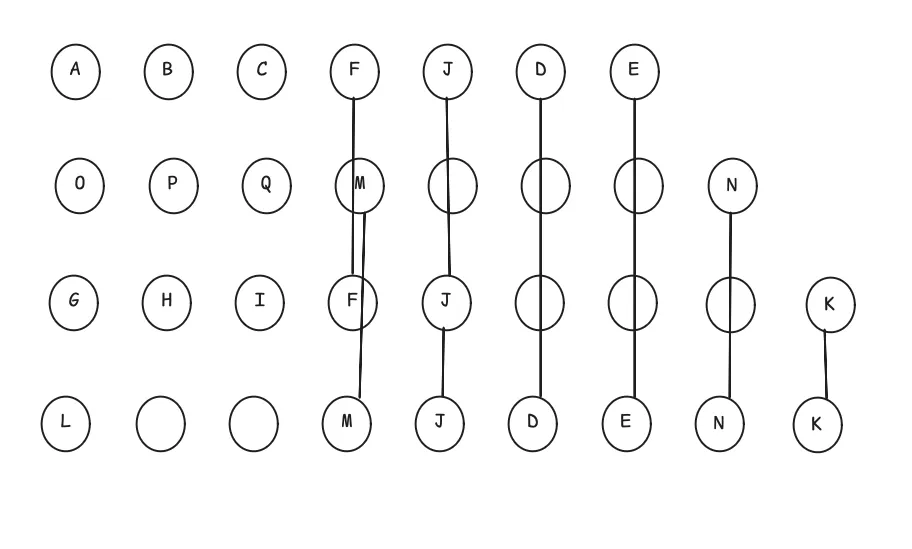使得空间利用最大化

感悟#

当思来想去，很复杂，也不是很清楚，于是到此我就查询了ChatGPT，于是才得知这是一个NP=P的问题，而且还有更简单的建模方法，叫图着色问题，然后有一系列的算法试图去解决它。

查了才知道，我这种属于启发式算法，在求解复杂问题时，不追求“绝对最优解”，而是使用基于经验、规则或贪心策略的近似方法，以较低计算代价快速得到“足够好”的可行解。还是有一定意义的。

怎么说呢，有种凭自己接触到边界的感觉，这种感觉还挺少有的，当晚可能脑子太兴奋了，以至于晚上2，3点才睡着。

怎么说呢，这篇博客写于一个应该复习算法考试的下午，只是简单的记录一下一次思考吧，我感觉我的博客也可以添加进去这些。