Lecture8 CNN Architectures

AlexNet#

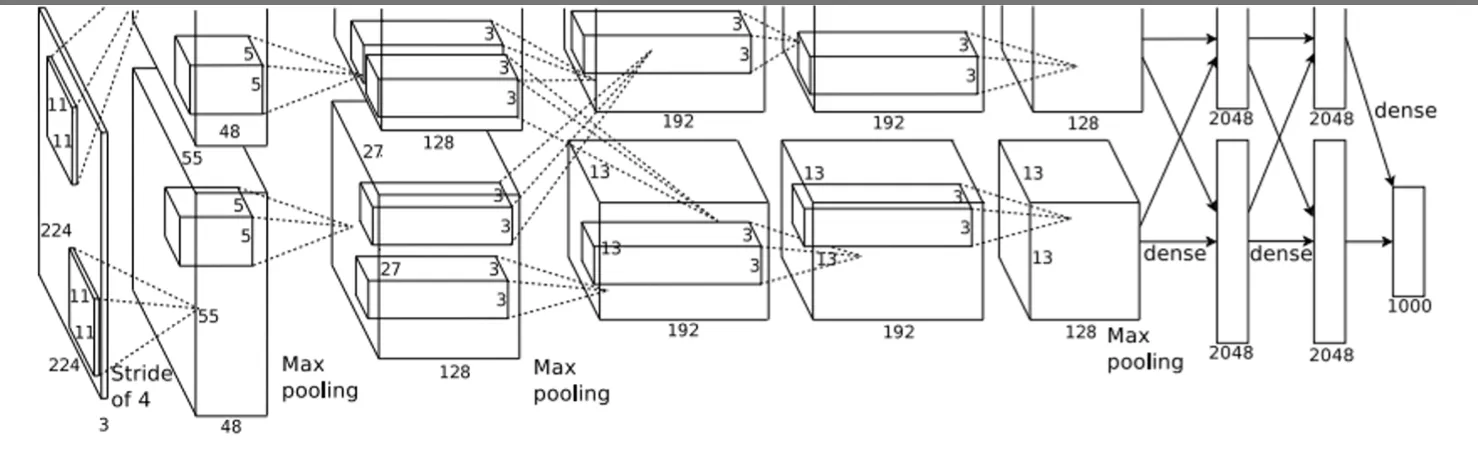alt text 这是最早的卷积神经网络，参数如下

227 x 227 inputs
5 Convolutional layers
Max pooling
3 fully-connected layers
ReLU nonlinearities 他这里Trained on two GTX 580 GPUs – only 3GB of memory each! Model split over two GPUs

值得一提的是需要知道的是模型的计算量(FLOPs)，参数量(Params)，占用内存(Memory)。这些和训练及其相关，当你更改神经网络的结构的时候，如果你希望公平对比性能、避免引入冗余，你需要确保计算量（FLOPs）基本持平。 alt text 这里拿AlexNet的卷积层为例子

Memory：#

\begin{aligned} \text { Number of output elements } & =C * H^{\prime} * W^{\prime} \\ & =64 * 56^* 56=200,704 \end{aligned}

Bytes per element = 4 (for 32-bit floating point)

\begin{aligned} \mathrm{KB} & =(\text { number of elements }) *(\text { bytes per elem }) / 1024 \\ & =200704 * 4 / 1024 \\ & =784 \end{aligned}

Params：#

\begin{aligned} & \text { Weight shape }=C_{\text {out }} \times C_{i n} \times K \times K \\ & =64 \times 3 \times 11 \times 11 \\ & \text { Bias shape }=C_{\text {out }}=64 \\ & \text { Number of weights }=64 * 3 * 11 * 11+64 \\ & \qquad \begin{aligned} & =23,296\end{aligned}\end{aligned}

FLOPs#

alt text 这里值得一提的是他们把一个乘法和一个加法看作一个运算，因为现在的设备已经可以在一个时钟周期里面完成这两个运算

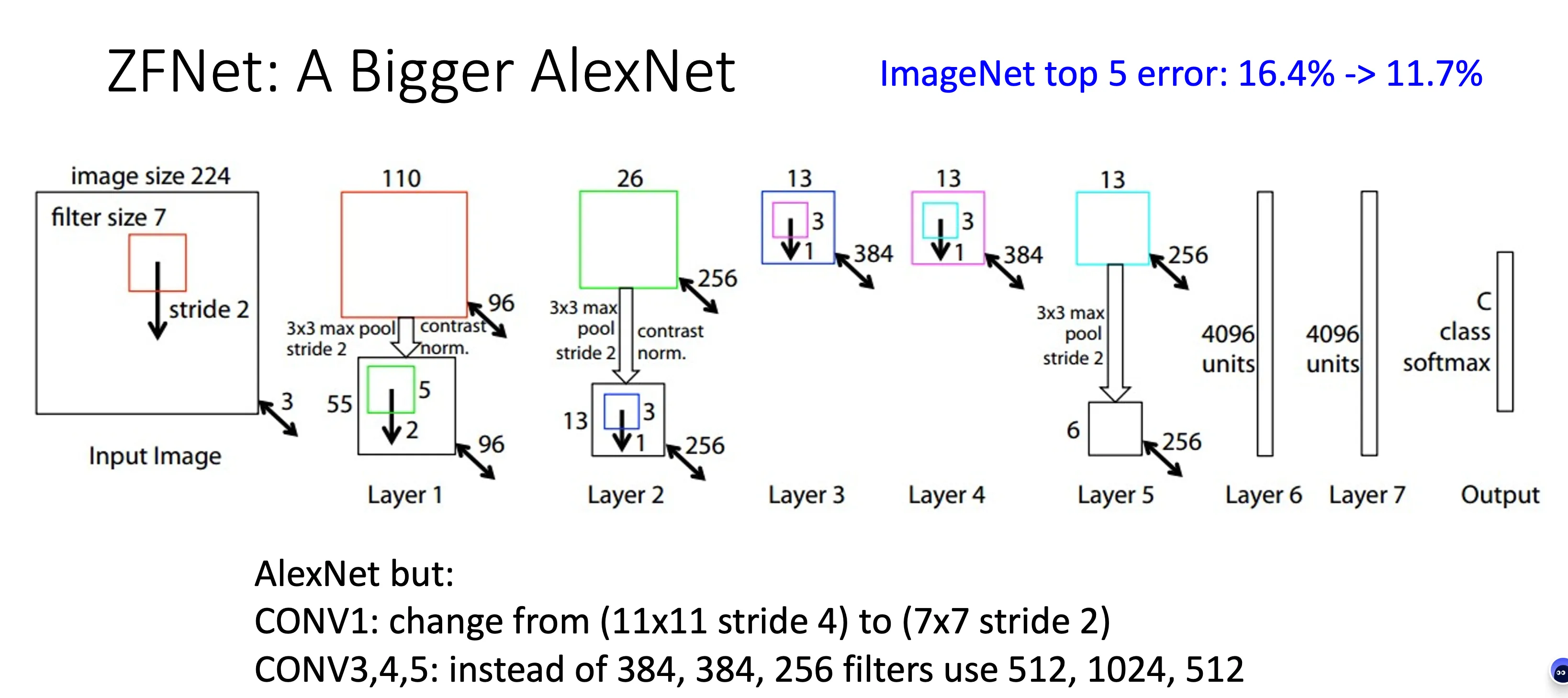
ZFNet#

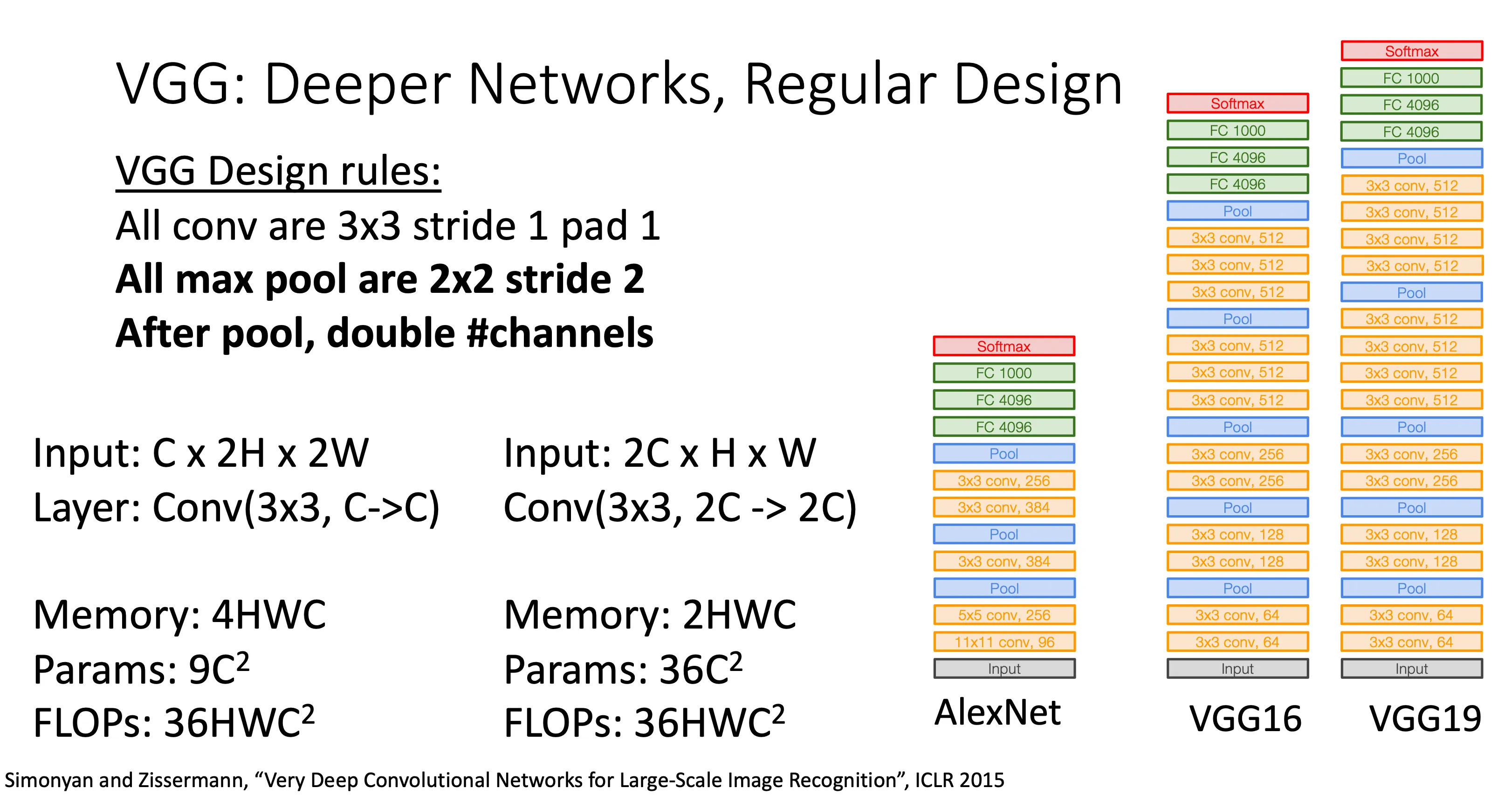
更大的AlexNet alt text

VGG#

alt text

他的改进之处就是相比于前两个，他更规范，意思就是前两个每个层的超参数以及怎么知道在哪个地方放什么层，这些都是Trial and error反复试错的结果，一旦我想要更大规模的结果，我就要重新Trial and error这些配置。所以VGG就把这个规范化，就有一个design rules(如上图)，然后这样子就方便扩大网络的规模。

GoogleNet#

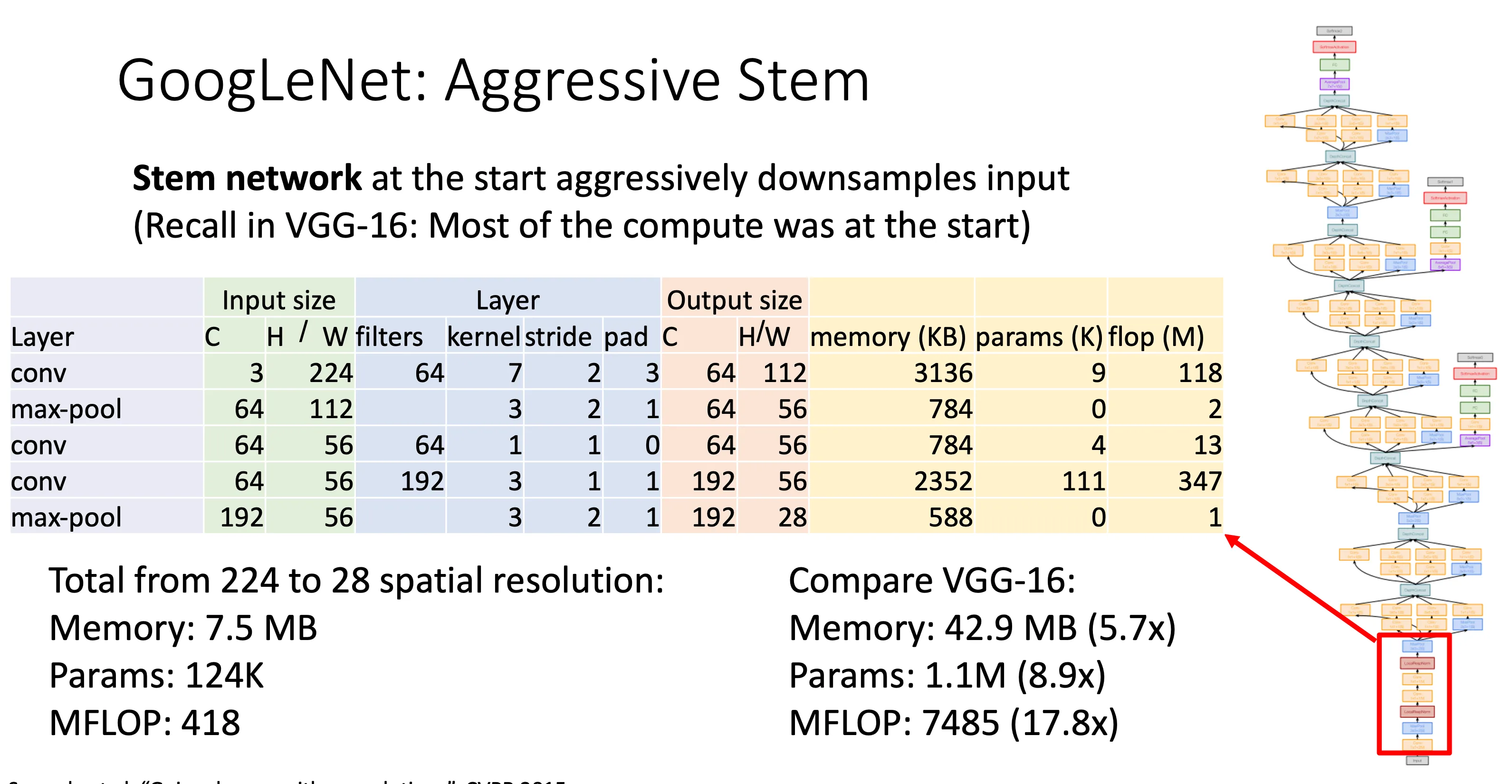alt text 这里最值得提的是，他没有一昧的追求扩大模型规模，而是关注模型的效率，他把最后的全连接层去掉了，而是用一个全局平均池化（GAP）来代替 GAP 是一种 把整个特征图（feature map）直接变成一个数 的方法，它对每个通道取平均值：假设某一层输出为大小 H×W×C 的特征图
→ GAP 会对每个通道 c 求： $y_c=\frac1{H⋅W}\sum_{i=1}^H\sum_{j=1}^Wx_{i,j}$ 最后变成一个长度为 C 的向量，作为最终的输出（可直接接 Softmax）。好处就是极大的减少了计算量，因为全连接层的参数量是最大的，想想全连接层中的矩阵，节约了这些的计算量

但是模型发展到这里遇到了瓶颈，当你堆叠很多层神经网络时，理论上模型应该越来越好，但实际中会出现：

训练误差先下降后上升（不是过拟合，而是梯度消失¹、优化困难）
网络越深，反而效果变差（退化问题²）为了解决这个问题，著名的残差神经网络(Residual Networks)就发明了(何恺明就提出的)

Residual Networks#

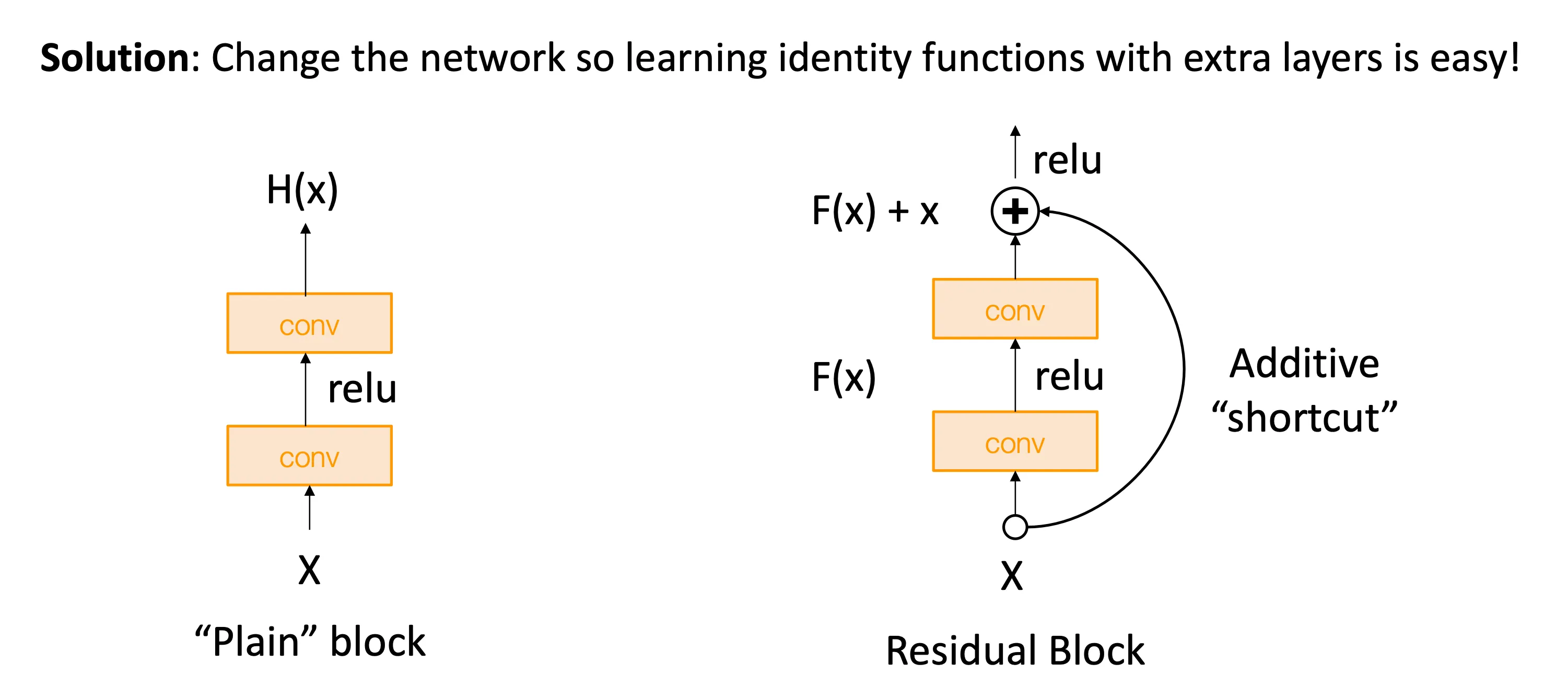alt text 灵感就是越深的神经网络却不如浅的神经网络，意味着神经网络甚至很难学到恒等函数，直接将浅层搬到深层中，然后让其他层都输出输入，理论上就得到和浅层一摸一样的网络。

但是问题就是很难学到恒等函数，残差神经网络的思想就是将输入直接跳过中间的层直接加到输出中，这样做的意义是：如果模型最优的输出就是输入本身，那它只需要学 F(x)=0 就可以了，比起直接拟合复杂函数更容易。

然后这就有一个问题残差连接只保证深层网络“不比浅层差”，但它凭什么就一定能“更好”？

答案就是：

1. 残差连接解决的是优化困难

没有残差连接时：网络越深越难训练（梯度消失、退化）
有了残差连接后：深层网络不再难以训练了，你才能“有可能”学得更好

也就是说，不是残差让网络更强，而是它让深层网络“有机会”变强

为优化器提供了更大的函数空间，理论上模型能力更强

意思就是模型可以学到更多的函数，有时候不需要很复杂的函数，这让网络可以灵活决定要不要学习复杂变换

在反向传播（Backpropagation）时，深层网络中的梯度在一层层传播回去的过程中变得越来越小，最后几乎为0，导致：前面几层的权重几乎不更新，收敛非常慢，甚至根本无法学习 ↩
当你加深神经网络层数时，理论上模型表现应该更好，但实际上会出现:训练误差反而更高,模型不如浅层网络,不是过拟合，因为训练集上都学不好。这是因为：网络太深，优化难度变大，层数多了反而“干扰”了已有特征的表达。 ↩