Lecture6 BackPropagation

Computational Graphs#

之前提到我们不断训练模型的时候，我们希望模型中的权重能够朝梯度下降的方向进行调整，我们通过损失函数来定义当前的这些权重好不好，然后我们希望损失函数计算出来的结果越来小，因此我们的权重希望能够朝着梯度下降的方向调整。

这时候我们就想要获得损失函数上点的梯度，以便我们向着梯度减小的方向调整参数。那这时候就产生一个问题，我们怎么计算梯度，一个想法就是暴力，对这个损失函数硬算梯度，但是这种方法显而易见的很不计算机，对于每一个损失函数，我们都要计算一遍梯度，也并不是很模块化。所以我们就有了反向传播算法计算梯度。

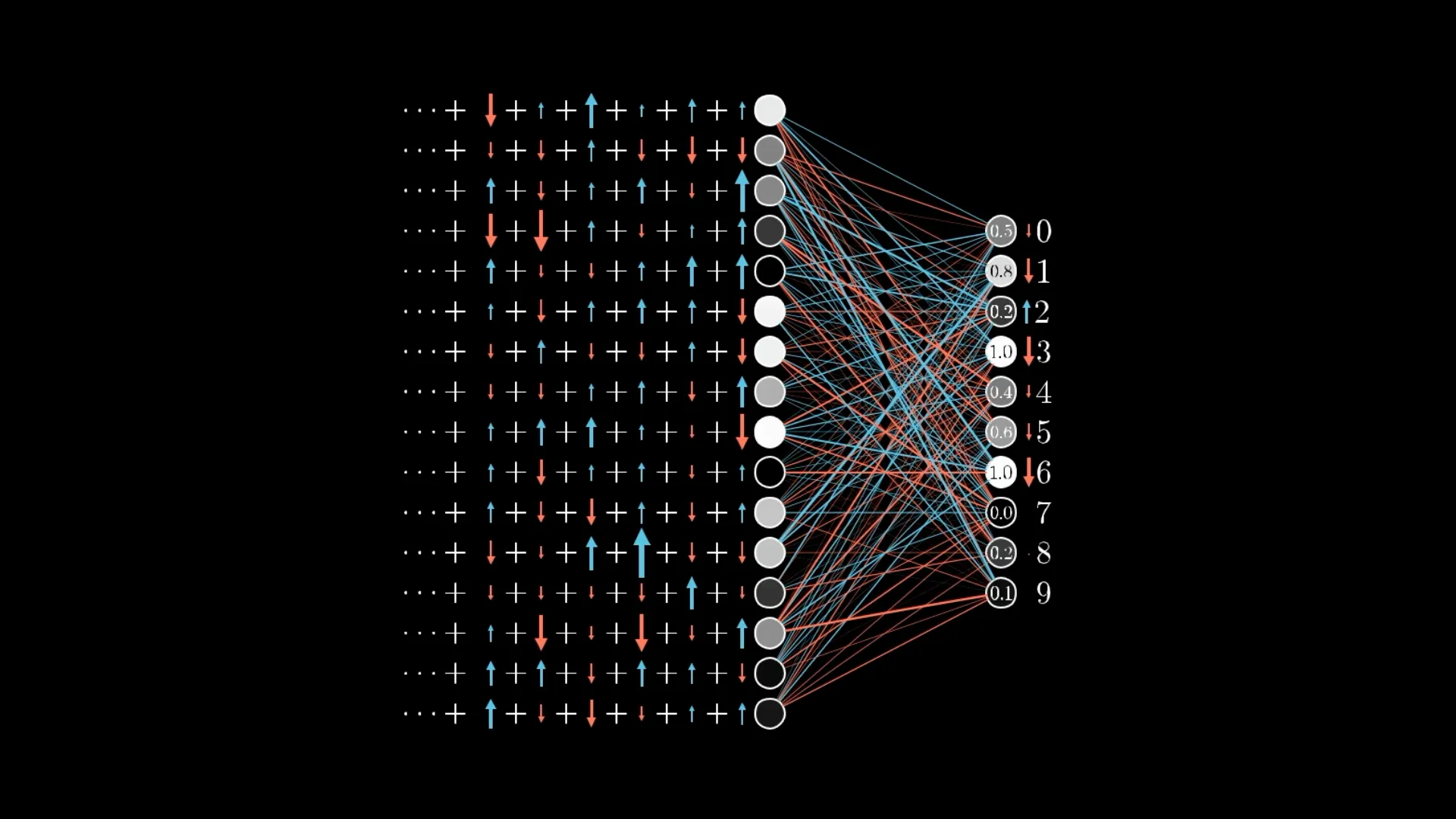
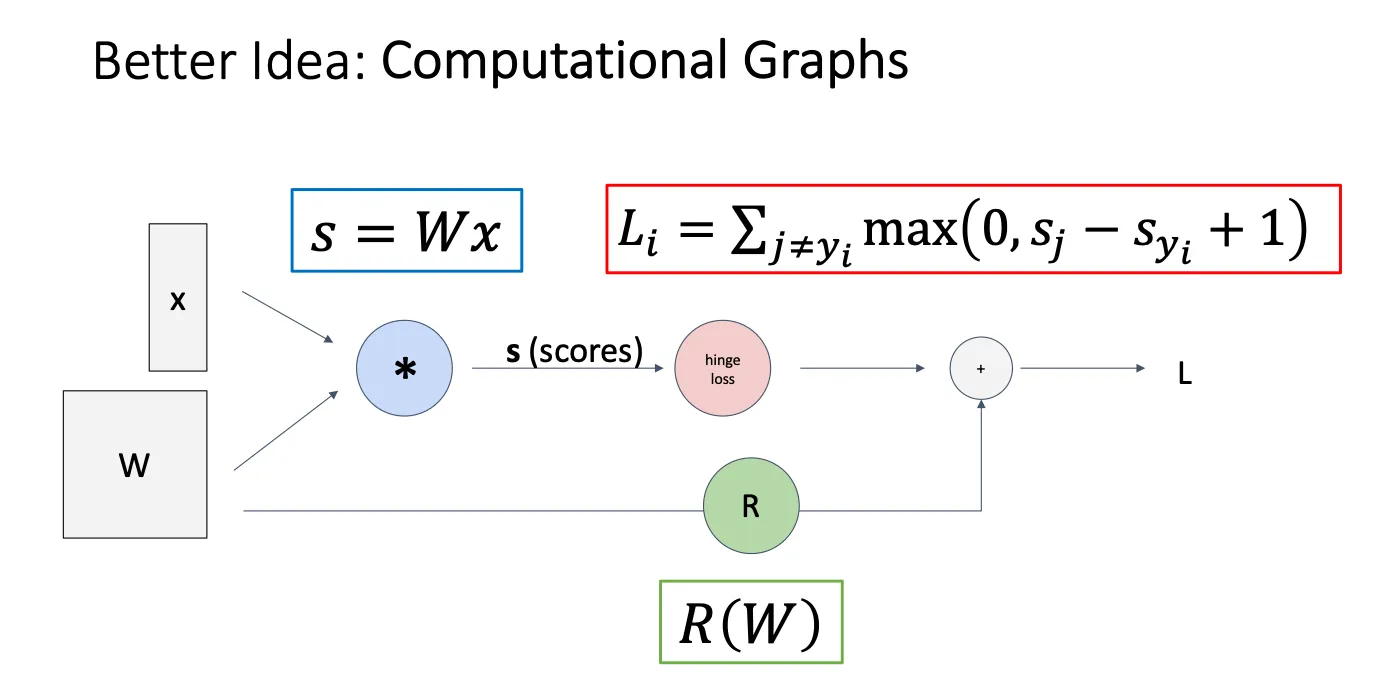
我们用Computational Graphs来表示我们模型的内部结构，包括输入的x，权重矩阵W，正则化R，最后的到我们的损失函数L

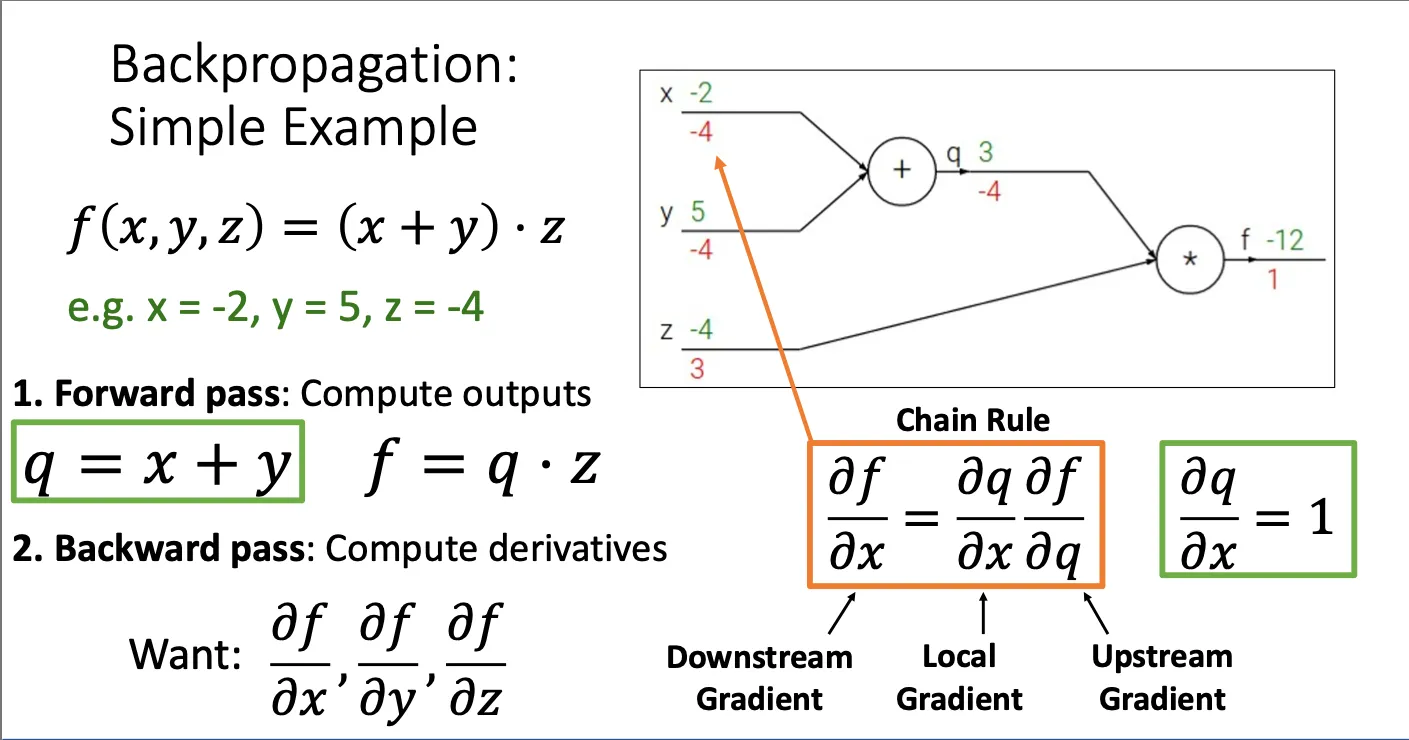
举个例子说明一下反向传播算法是怎么实现的：

假设现在我们有一个损失函数$f(x,y,z)=(x+y)z$ 然后现在我们想求$x=-2,y=5,z=-4$ 这个点的梯度是什么，然后我们先进行的是forward pass，就是计算出之后的结果，q等于什么，f等于什么 之后进行backward pass，算出相邻后一个对前一个的导数然后一步步往下推，本质上就是链式法则。这种做法的好处就是非常的模块化，每一个节点的计算不再看其他节点是什么，只用看传到这个节点的导数是什么并传递给下一个就可以。我们给每个点要处理的导数命名，downstream gradient，local gradient，upstream gradient。

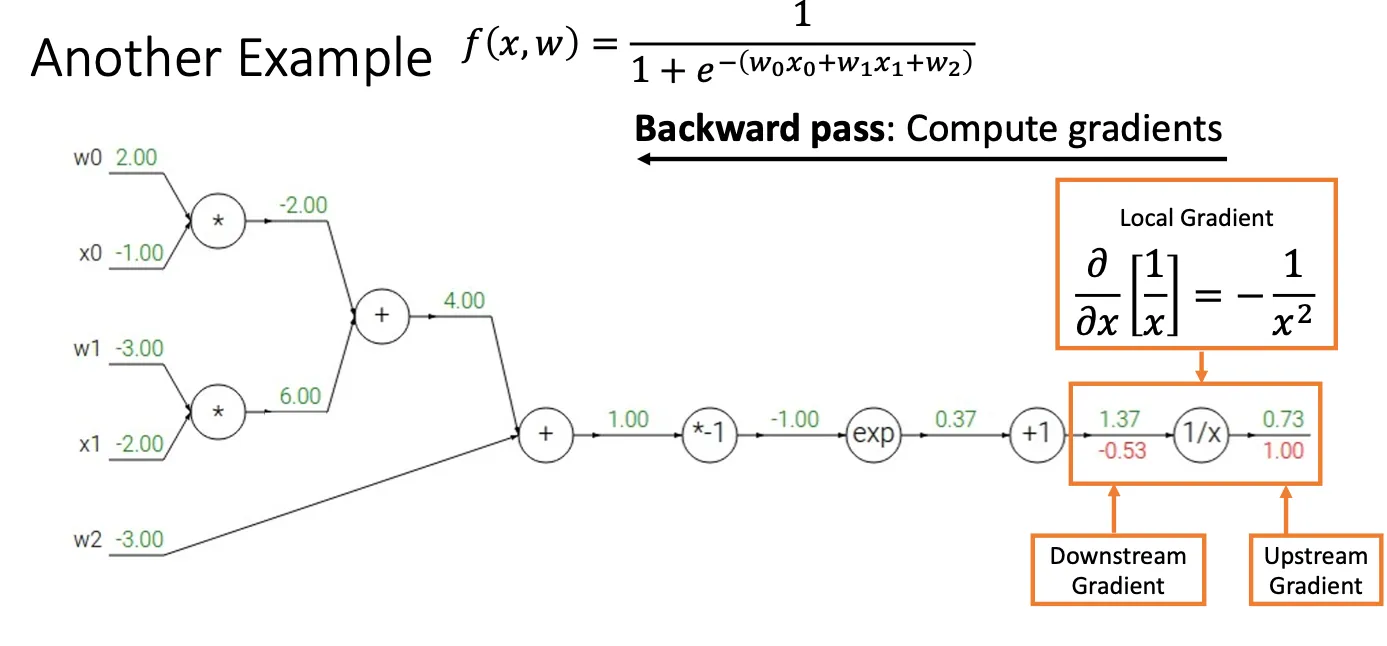
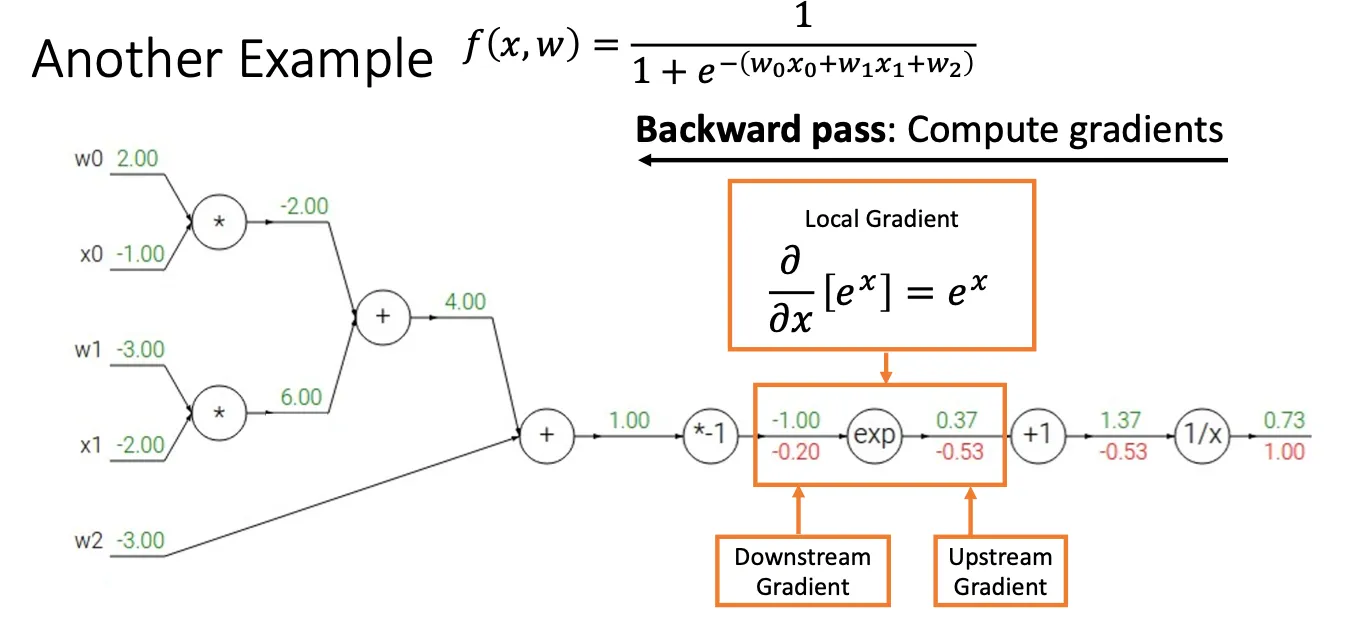
下面看一个再复杂的例子： 对于图中框出来的那个节点，假设前面所有的节点统一为x，当x经过倒数运算的时候，他得到了最终结果f，简单来说就是$f=\frac{1}{x}$ 然后我们想计算 $\frac{ \partial f }{ \partial x }$ 然后当前x的值为1.37，所以最终结果就为$-\frac{1}{x^2}=-\frac{1}{{1.37}^2}=-0.53$
再看后面： 我们再次把框中节点以前看作x，他经过$e^x$ 操作之后得到结果p($p = e^x$ )，然后我们想知道 $\frac{ \partial f }{ \partial x}$ 但这时候我们的计算方法就是 $\frac{ \partial f }{ \partial x} = \frac{ \partial p }{ \partial x}* \frac{ \partial f }{ \partial p}$ ,然后$\frac{ \partial f }{ \partial p}$ 已经一步一步传下来了-0.53，所以我们在当前节点中计算$\frac{ \partial p }{ \partial x}$ 因此得到$\frac{ \partial f }{ \partial x}$

改进#

根据这种计算方法，我们发现一些函数普遍的出现在模型中，比如图中蓝色框出来的部分，s型函数，这个函数挺普遍的，然后他的梯度的公式也很简单，于是我们就可以将这种函数压缩成一个节点，直接用先前算好公式带入，而不是将这些节点拆分的非常原子。这种做法的好处就是我们可以不用再存这么多节点，也不用每次都计算一下这个函数的梯度，可以加快反向传播的速度。

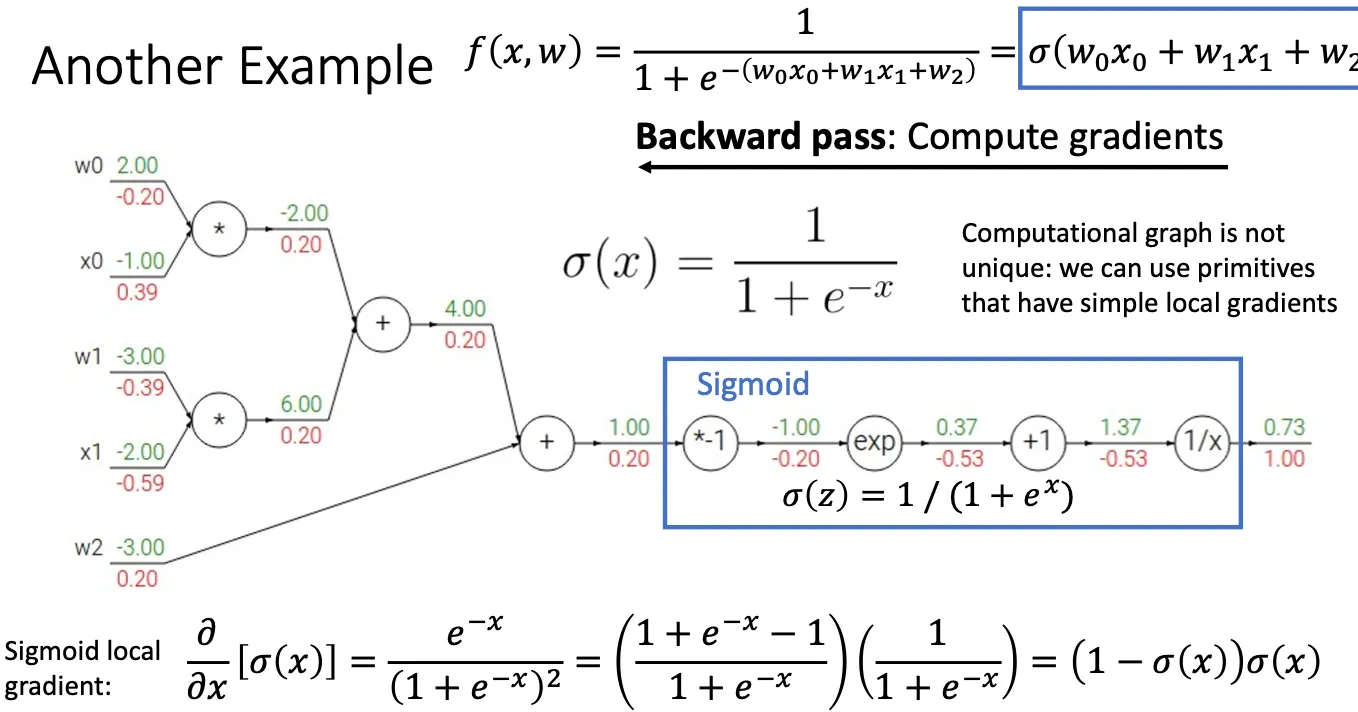
现在我们就可以将很多种这些运算封装成一个个函数，这样当我们需要进行某个运算的时候我们直接调用就可以。这样子我们就实现模块化设计，不用根据每种损失函数都些一遍代码。

Vector#

上面到目前为止都是标量的计算，我们求的是损失对标量$x$ 的导数，但是在实际的神经网络中我们的输入是一个一维的向量，这表示一个图片。然后我们要求的是损失L对W的导数，对X向量的导数，准确来说一般称之为梯度而不是导数。

假设现在我们中间某个节点有 $y=xw$ 然后这些都是矩阵，我们从上游传递到这个节点的导数是$\frac{dL}{dy}$ 然后我们想计算一下L对x的导数和L对w的导数，然后这就是他们的公式，但是很奇怪x和y不应该都是向量吗，为什么这里都是矩阵。

视频中还提到一点就是我们显示计算每个矩阵的雅可比矩阵然后来相乘，意思就是我们不会先计算出整个雅可比矩阵 J 再与 $v^T$ 相乘，而是直接逐步计算结果。

感觉视频讲的有点云里雾里的，不如deepseek举个例子

正向累积（Forward Accumulation）&& 反向累积（Reverse Accumulation）#

对于计算梯度而言，我们的式子可能是这样

$$\frac{dL}{dx_0}=\frac{dx_1}{dx_0}\frac{dx_2}{dx_1}\frac{dx_3}{dx_2}\frac{dL}{dx_3}$$

这时候就有两种顺序来算这个链式法则式子，一个是从右边往左边算，一个是从左边往右算，前者就是反向累积，他的意思就是对于一个计算图，我们从计算图的右边每次逐渐计算到左边

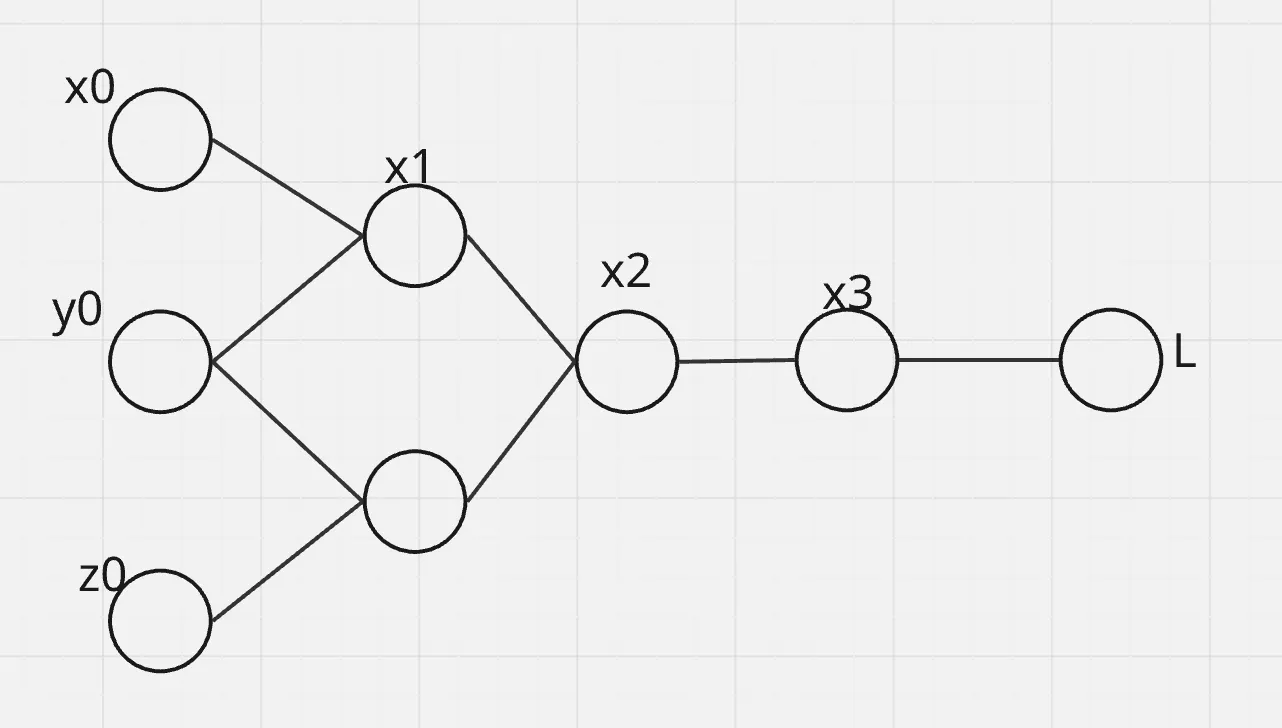
然后这种顺序所需要的就是一开始前向传播的时候我们要记住中间值，时间复杂度为O(n),空间复杂度也为O(n)。

然后前向累积就是先计算式子左边，然后推到式子右边，这种方法相比之下就不需要存储中间值，从最左边开始不断向右求导，空间复杂度为O(1),但是这种做法的坏处就是对于每一个变量$x_0,y_0,z_0$ 而言，他们各自的梯度都要单独算一遍，也就是说假设有m个变量，他的时间复杂度就是O(mn).