Lecture7 Convolutional Networks

Filter#

当我们将一张图片压缩成一个一维的长向量的时候，这个图片的空间结构被破坏了。

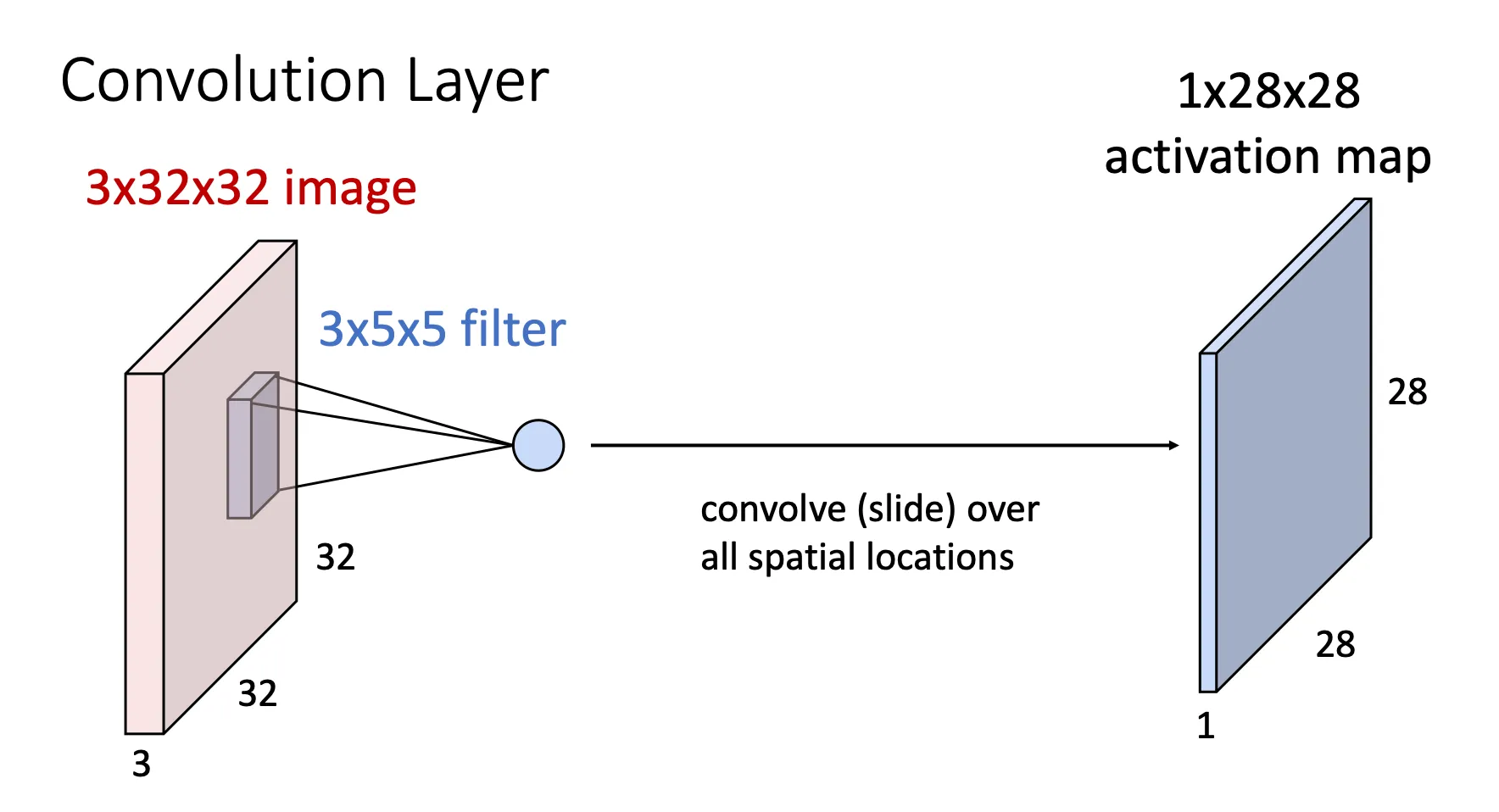
所以，为了解决这个问题，就有了Convolutional Networks（卷积网络），我们将图片转化成3*32*32的张量（假设图片是RGB三原色，32*32长和宽），其中3表示的是depth/channels。

这时我们用filter（卷积核）来处理这个图片，filter也和图片的depth一样，大小这里取了5*5 然后用这个filter和图片的每一块进行内积，用这个filter扫过这个图片，每次扫的区域经过内积得到一个数，然后这些结果就可以形成另一个depth为1的张量，一共有28*28的区域相内积。所以我们得到一个1*28*28的图。

Filter layer#

事实上，我们并不是只有一个filter，我们有很多个不同的filter，每一个filter都扫一遍这张图片，得到多个activation map，当多个filter堆在一起的时候，我们就有卷积层。filter的数量就是一个超参数，可以自定义。这个卷积层就是一个4维的张量，计算出的activation map就是一个三维的张量。还有就是每一个filter都有一个偏移量，当filter和图片中的每一块内积完之后要加上这个偏移量，于是这些偏移量组成一个向量。

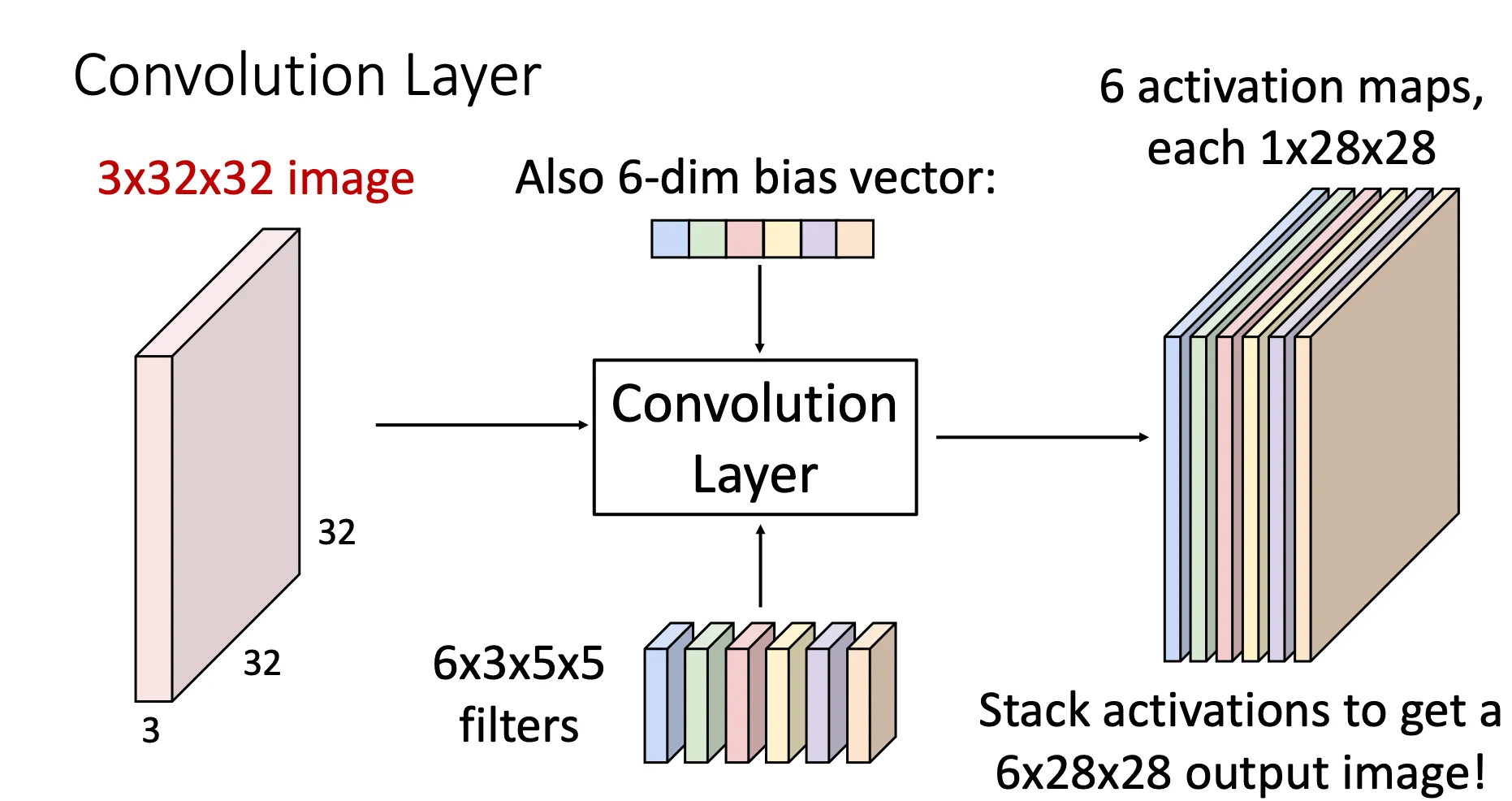
每一个activation map都可以看作是图片的某种特征的集合，他们通过filter将这些特征提取出来组成一个集合，这些特征反应的就是图片的空间信息。

我们的输入可以不只是一个三维的张量，我们可以有多个三维的张量，形成一个四维的张量，对图像的进行批量处理。所以卷积层的一般性就长这样。

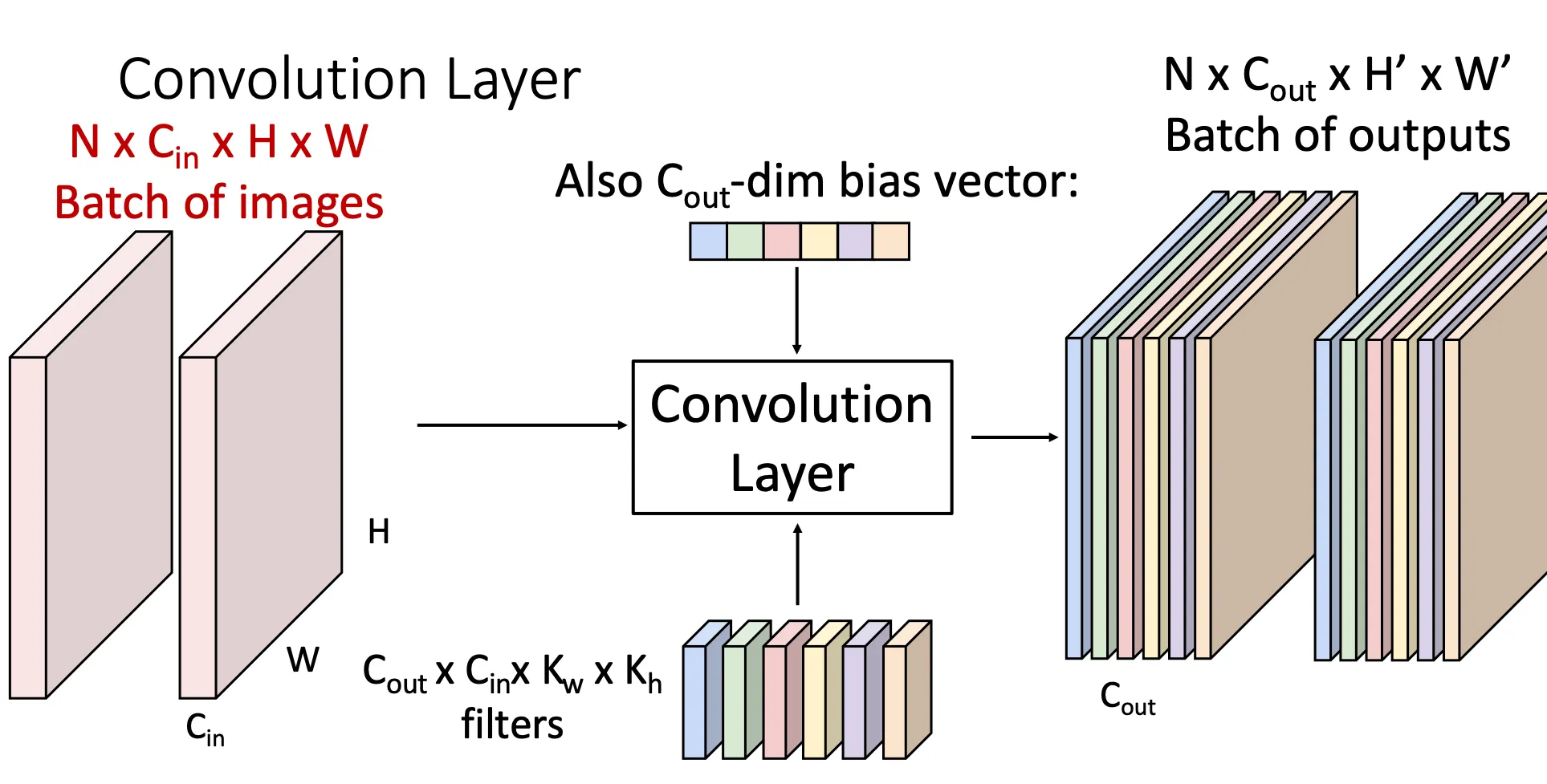
然后，我们就可以抛弃原本的那种神经网络，之前的权重矩阵W不再只是和一维向量的一次线性组合。而是变成filter，于是我们就由Linear Classifiers 转变成卷积神经网络。每一个图片经过filter的运算后再经过激活函数，这样就既可以保留图像的空间信息，又避免只是线性的进行分类。

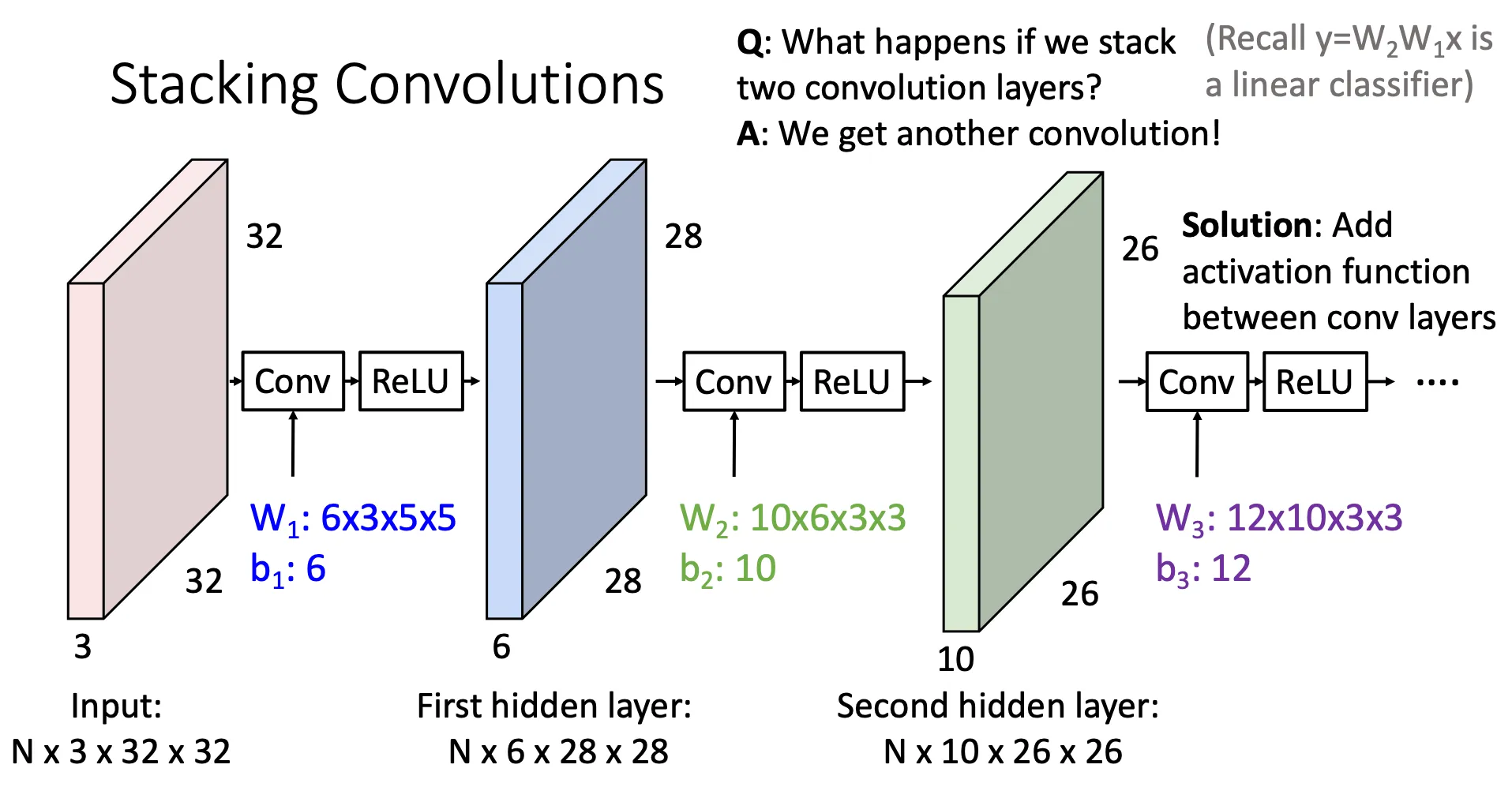
Pedding#

值得注意的是，当我们将一个图片经过一个卷积核处理之后，他的大小就会减小，假如我们的图片是M*M的，我们的卷积核是K*K的，那么我们最后的图片就是（M-K+1）*（M-K+1）的，意味着每经过一层卷积层我们的图片大小就会减小。因此提出一种方法，我们对图片进行一个填充，给图片的外围填充一圈，然后再进行卷积操作。其中有不同的填充策略，比如外围全都用0来填充就叫zero pedding。一般来说zero pedding很通用，效果也很好。还有一个超参数P是填充层的层数，一般来说经过处理后图片的大小是（M-K+1+2P）*（M-K+1+2P），然后P就是$\frac{k-1}{2}$ ,这样可以保证输出的图像的大小和之前的一样。这种填充方式就叫same pedding。

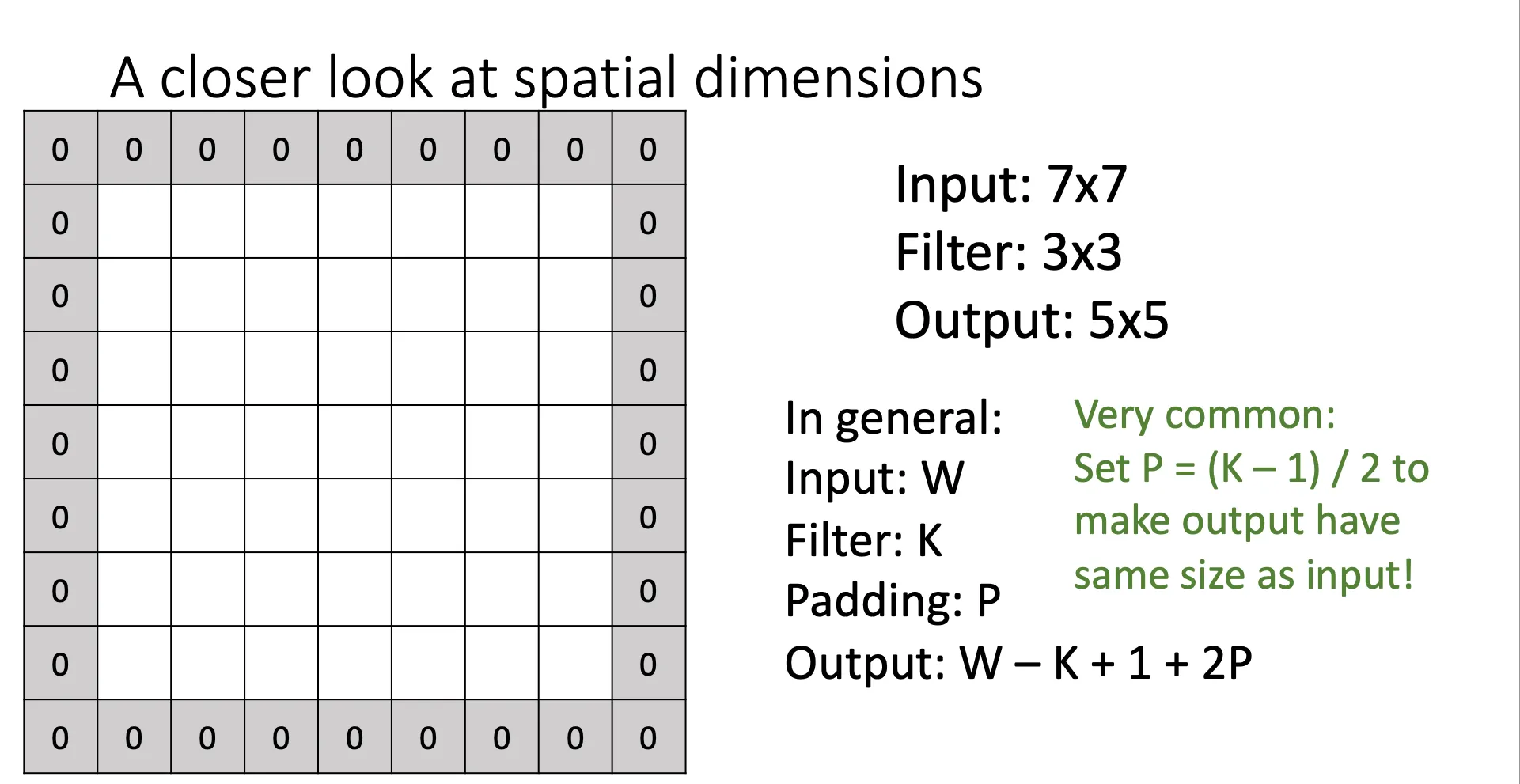
Receptive Field(感受野)#

感受野（Receptive Field）指的是神经网络中某个神经元或卷积层神经元所能“感知”到的输入数据区域的大小。简单来说，感受野描述了每个神经元在输入图像上对应的区域大小，或者说它所能获取的信息量。

具体来说：

1. 卷积神经网络（CNN）中的感受野：在卷积神经网络中，感受野通常指的是输入图像中经过若干卷积层后的某个特定神经元能够“看到”的区域大小。随着网络的深度增加，每一层的神经元会连接到更大的区域，从而扩大感受野。

2. 感受野的扩展：通常情况下，通过增加卷积层的数量或者增加每一层的卷积核大小，可以扩展感受野。例如，如果第一层卷积核是3x3，第二层也是3x3，那么第二层的每个神经元就能感知到更大的输入区域。

3. 感受野的重要性：感受野越大，网络就能捕捉到输入数据的更多上下文信息。对于一些任务（比如图像分类），需要较大的感受野来捕捉全局信息；而在一些更注重细节的任务（比如目标检测）中，较小的感受野可能更合适。

Stride(步长)#

有的时候我们想要快速的快速降低特征图尺寸的任务，或者希望更快速地捕捉全局信息的任务。比如我们有一个1024*1024的图片，那么我们就要有一个很多层的卷积层来对他进行处理。

这时我们就引入一个新的超参数 步长（stride）这个的作用是控制每次卷积核扫过图片的速度。以前的话当我们用步长为1的话，他就会遍历，每次只移动一个单位，但是当我们调整我们的步长的时候，他可能就每次移动2个或更多的单位，我们就可以更快的扫完整个图片，快速的减少每一次卷积之后图片的大小，同时也保留图片的特征。这时他也就可以更快的增加感受野，然后处理过后的图片的大小就是（W-K+2P）/S+1。当然如果这个S不能刚好被整除，那么这就可以向上取整，截断等等。但是通常情况我们会将S设置的刚好可以被整除。

1*1 filter#

在卷积神经网络中，1x1的卷积核（filter）是指卷积核的尺寸为1x1，也就是说它在输入的每个位置只覆盖单个像素点。虽然它的尺寸很小，但在实际应用中，1x1卷积核非常重要，具有多种功能和用途。

作用：

1. 通道间的混合：

   • 最常见的用途之一是用于改变特征图的通道数（也就是深度）。1x1卷积通过将每个像素点的多个通道（特征图的深度）组合在一起，生成新的特征图。

   • 比如，假设输入有一个大小为 $H×W×C_{in}$​ 的特征图，其中 H 和 W 是空间维度，$C_in$​ 是输入的通道数。通过使用 1x1 卷积核，输出可以生成大小为 $H×W×C_{out}$​ 的特征图，其中 $C_{out}$​ 是输出的通道数。

   • 例子：假设输入特征图的大小是 32×32×64，我们使用一个 1x1 的卷积核，将通道数从 64 降到 32，那么输出的特征图大小将是 32×32×32。

2. 减少计算量和参数：

   • 1x1卷积的另一个优势是它可以减少计算量和参数数量，特别是在卷积网络中，其他大尺寸卷积（如3x3或5x5）的参数非常多。通过在卷积网络中引入1x1卷积，先减少通道数，再执行更大的卷积核操作，可以显著减少计算复杂度。

   • 例如，假设输入特征图为 H×W×256，通过一个 1x1 的卷积核将通道数减少到 64，然后可以进行 3x3 或 5x5 的卷积操作，减少了后续卷积层的计算量。

3. 非线性变换：
   • 1x1卷积还能实现输入特征的非线性变换，这类似于全连接层的作用，只不过是在卷积的框架下进行。每个像素点都经过一个1x1卷积进行映射，虽然每个位置的卷积核只有1个参数，但它能有效地将不同通道的信息融合。
4. 瓶颈层（Bottleneck layer）：
   • 在一些网络架构（比如ResNet和Inception）中，1x1卷积被用作瓶颈层。瓶颈层通过减少特征图的通道数来降低计算量和内存需求，然后再通过较大的卷积核（如3x3）进行特征提取。这样的设计可以加速训练和推理。
5. 增加网络的非线性能力：
   • 通过在1x1卷积后加入激活函数（如ReLU），网络可以增加其表达能力，进行复杂的特征转换和组合。

Pooling Layers(池化层)#

这部分的作用其实就是单纯的downsample（下采样），就是指通过某种方式减少数据的空间或时间维度，在图像处理中，通常是通过减少图像的分辨率来达到减少计算量和存储的目的。同时这一部分没有学习参数。

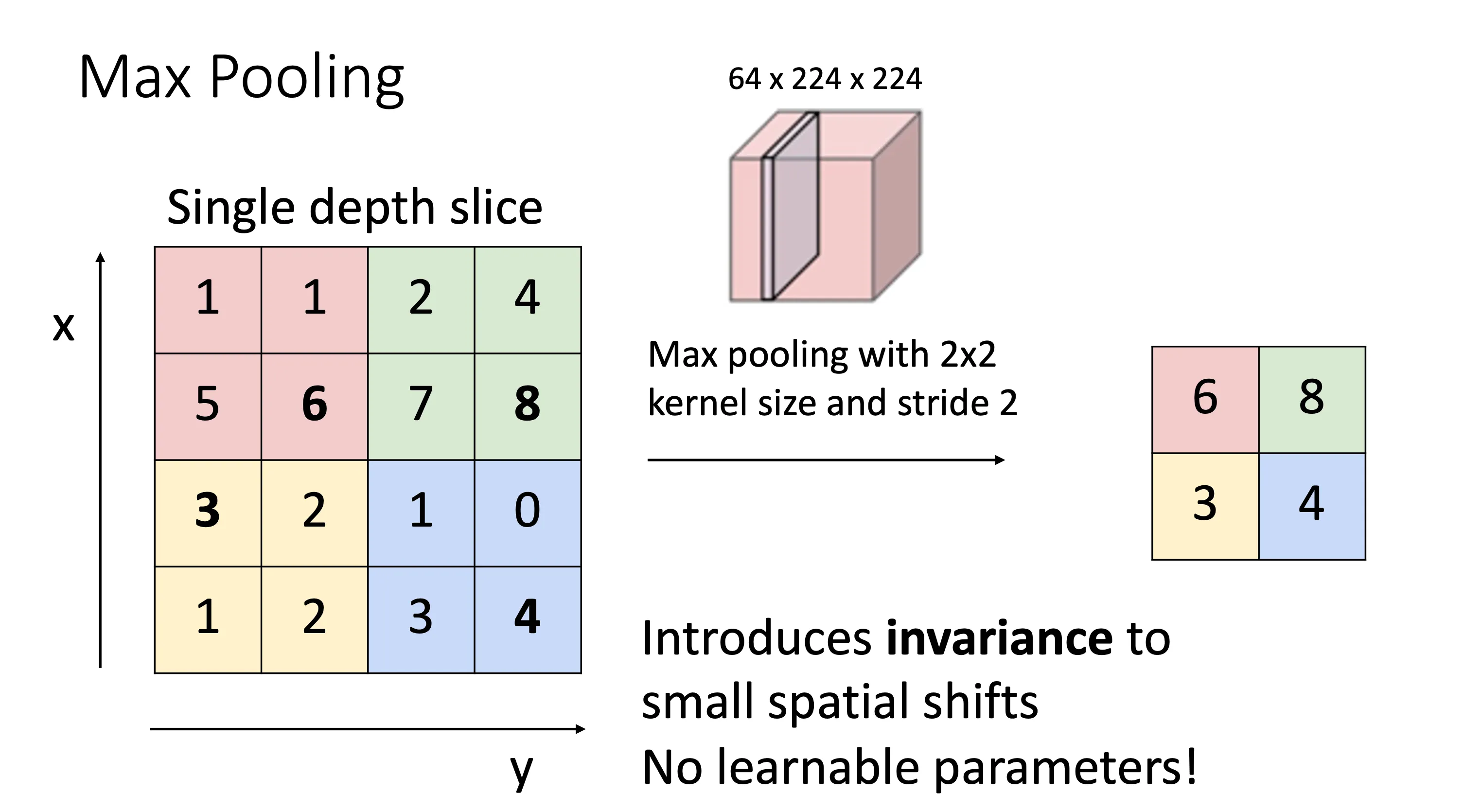
Max pooling#

这个就是给定一个n*n的 max pooling ，然后就计算图片中n*n的最大值，将一个n*n的数据downsample为一个数，一般而言我们将max pooling的步长设置为和size一样的大小n。这种方法某种程度上引入了一定的不变性，假设图片上面的某些东西轻微的移动了一下，那么这部分的max value可能不会有变化。

Average pooling#

类似就是选取这个区域的平均值

Convolutional Networks#

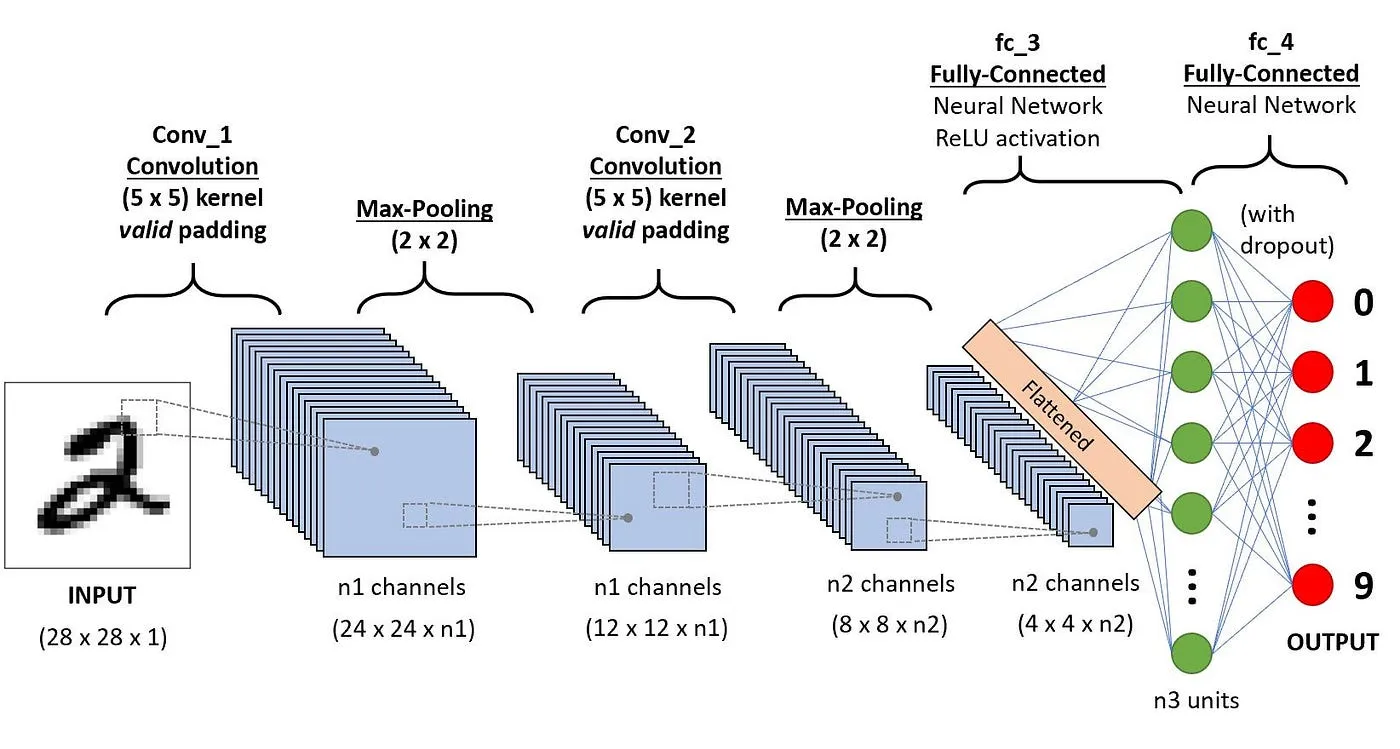
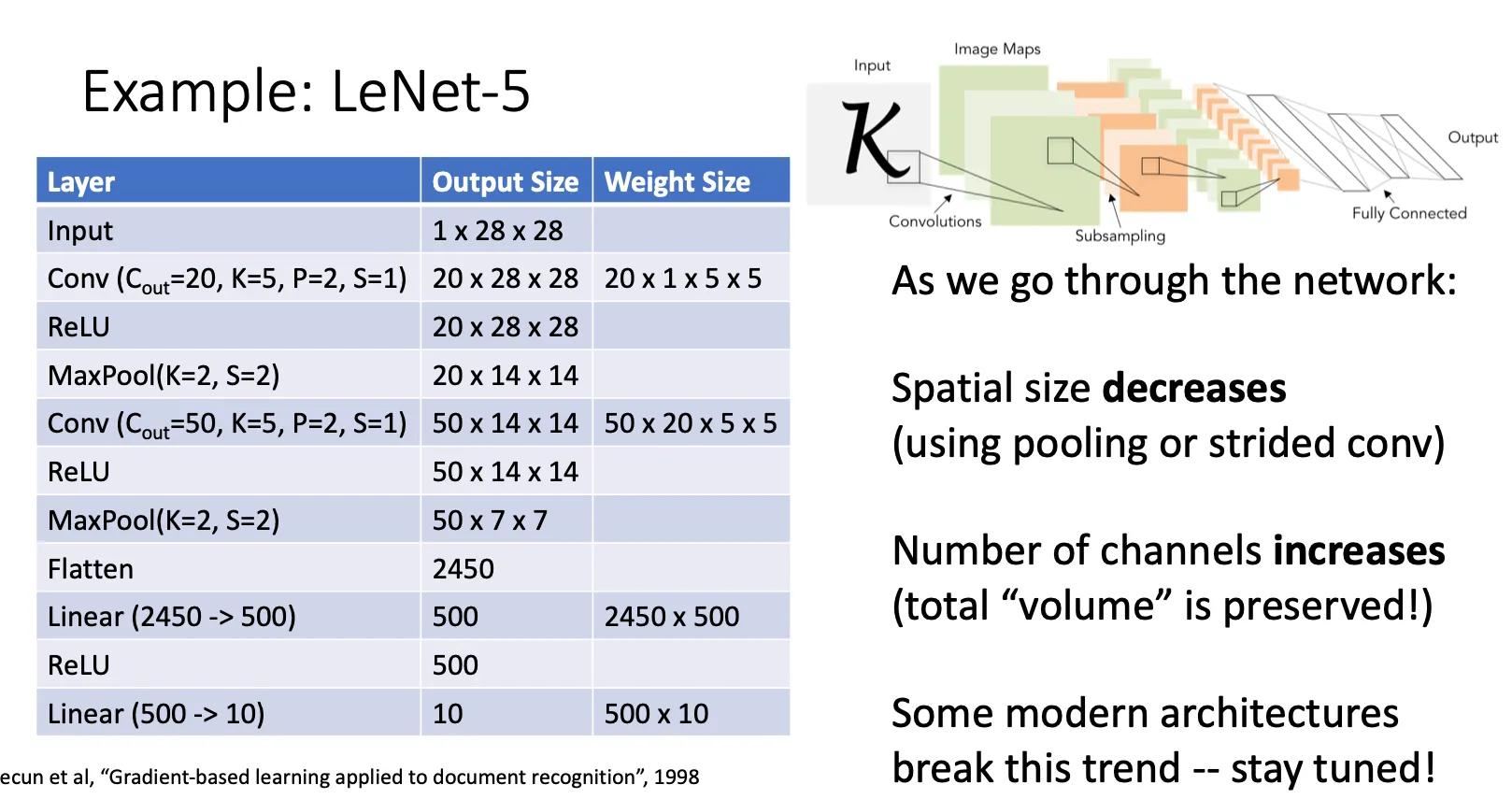如图，我们将卷积层，池化层，激活函数，全连接层全部连接起来，我们就得到大名鼎鼎的卷积神经网络，当然卷积神经网络不一定只有一种方式。 这里举杨立昆的LeNet为例子

1. 我们将一张28*28的一张灰度图，所以通道数就是1，先输入进卷积层，用的是same pedding，然后卷积层有20层，然后是5*5的卷积核
2. 之后经过激活函数处理
3. 再经过池化层
4. …
5. 值得注意的是后面有一个flatten的操作，将原本的50*70*70的图片转化成一个一维的向量，这样子就像之前的linear classifier一样，最终得到一个大小为10的一维向量，表示想要识别的标签

这里有趣的是我们在用max pooling的时候其实就已经引入非线性函数了，所以说其实ReLU并不是必要的，但是在现代的神经网络构建中仍然保留，表现你的神经网络的规范性。

Normalization#

当我们真正用这个传统架构去训练的时候，我们会发现一个问题，就是他十分难收敛，主要原因有说法是internal covariate shift。在深度神经网络中，每一层的输入实际上是前一层的输出。随着网络训练的进行，前一层的参数在不断变化，因此，后一层的输入数据（即前一层的输出）也会随之变化。这个过程可能导致神经网络的每一层都在不断地接收不同分布的输入数据。具体而言，训练中的每一层会接收到来自上一层的输入数据，而这些输入数据的分布是随着网络参数更新而不断变化的。 这种变化对训练过程产生了负面影响，因为：

1. 网络的每一层都需要不断适应输入分布的变化，这会使得梯度传播变得更加复杂和不稳定。
2. 网络的优化过程可能会变得非常缓慢，甚至会导致收敛性问题。
3. 神经网络的训练依赖于稳定的输入分布，而内部协变量偏移的存在导致这种稳定性丧失。 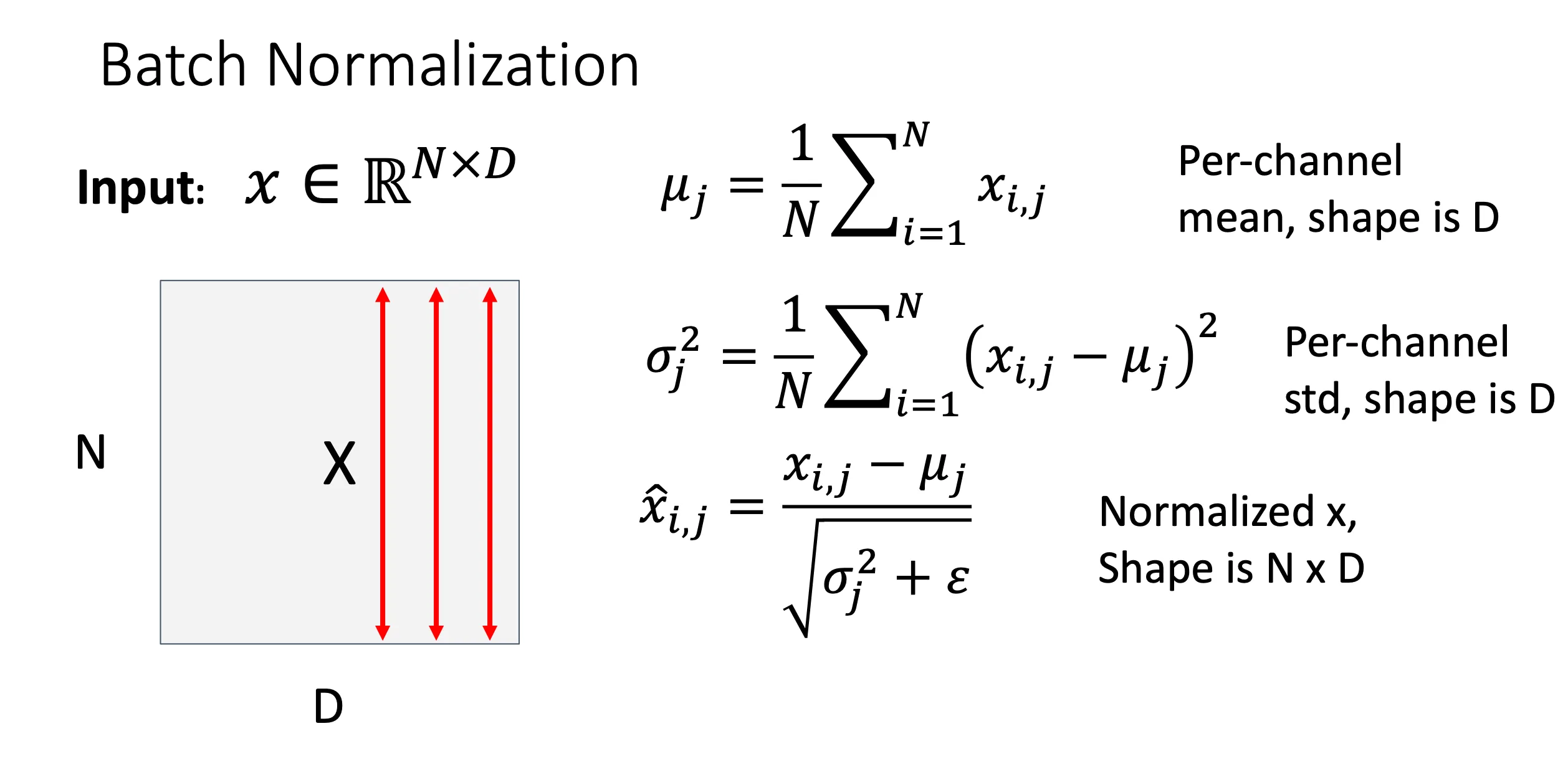如图，这里的计算就是假设我们有N个图片组成一个batch，然后每个图片是H*W*$C_{in}$
   然后在Batch Normalization的时候，他就会把N个图片，每一个图片的通道 $j\in C_{in}$ 的图片拿出来，这时候，这个图片就是一个H*W的二维的图片，然后对这些图片求和时候求均值，求方差以及标准化。具体来说$x_{i,j}$ 就是第 i 张图片，第 j 个通道，这是一个二维的矩阵，大小为H*W。

然后避免方差$\sigma^2$ 为0导致标准化的时候除以0，引入一个很小的 $\epsilon$ 。这种的变化下能使得每一通道的输入数据具有零均值和单位方差。

虽然标准化操作通过使每个通道的均值为 0 和方差为 1 来加速训练和提高稳定性，但这种标准化可能会限制网络的表达能力，特别是在需要特定数据分布的任务中。例如，假设网络需要某个通道的数据具有不同的方差和偏移量，这时标准化会让它失去灵活性。

为了克服这个问题，我们引入了缩放因子 γ 和 平移因子 β，这两个参数是可训练的，允许网络对标准化后的数据进行线性变换，从而恢复网络的表达能力。

具体来说，Batch Normalization 的输出是:

$$y_{i,j}=\gamma_j\cdot\hat{x}_{i,j}+\beta_j$$

• $γ_j$ 是第 j 个通道的缩放因子，用来控制标准化后的数据的方差。
• $β_j$​ 是第 j 个通道的平移因子，用来控制标准化后的数据的均值。

通过这两个参数，网络可以对每个通道的数据进行自由缩放和平移，恢复网络的学习能力，并根据具体的任务需求进行调整。

但是这样又有一个问题：

• 训练阶段： 在训练过程中，我们每次使用一个批次的数据进行计算，并计算该批次的均值和方差。这意味着每个批次的均值和方差是根据该批次的数据来计算的。由于训练中的数据是动态的，批次之间的分布可能会有所不同。因此，每个批次的均值和方差也会有所不同。
• 测试阶段： 在测试阶段，通常输入数据是单独的一张图片或一个小批次的数据。由于测试数据量较少，而且分布通常与训练时的批次分布不同（例如，测试集上的数据可能比训练集更加均匀），如果仍然使用测试时的批次级别的均值和方差，会导致不稳定的预测结果，因为这些均值和方差无法代表整个训练集的统计信息。

所以为了确保 测试时的标准化稳定性，在训练过程中，我们会计算并保存每个通道的 全局均值 和 全局方差。这些值是在训练过程中，基于所有批次的统计数据，计算出来的。这些全局统计量是固定的，用于测试时的数据标准化。具体来说：

• 在训练时，我们会根据每个批次的均值和方差来更新全局均值和方差。
• 在测试时，我们不再计算当前批次的均值和方差，而是直接使用训练阶段积累的全局均值和方差。

这样做还有一个好处就是当测试的时候这些均值和方差就是常数了，所以Normalization这一步就相当于一个线性变换，于是我们就可以将这一步和前面的卷积融合在一起，直接融合到卷积核里面，于是好处就是我们节省了Normalization这一步的开销。

Normalization的好处有很多，比如他可以加快训练速度，我们可以因此加快学习率等等 但是这个理论仍然没有很好的被理解，到底是为什么，就像是一个实验性的结论，还有就是我们要在训练和测试的时候替换那个均值和方差，这可能是很多程序bug的来源。

The essence of Convolutional in deeplearning#

当我们看待深度学习中的卷积的时候，我们的卷积核其实就是一层小的模版，当我们用这个卷积核扫过图片的每一部分的时候，实际上我们是想看图片的这一块区域和这个模版是不是相像。举个例子假如说我们现在有一个3*3的卷积核

$$\begin{pmatrix} -1 & 0 & 1\\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{pmatrix}$$

当我们用这个卷积核去扫图片中每个3*3大小的区域的时候，这个区域和这个卷积核做内积，也就是说，当这个区域符合这种第一列为负数第三列为正数的时候，他们之间的内积就会变得很大。如果说这个区域的颜色都是相同的时候，内积的结果就是0。这实际上相当于识别图像的竖向向的边界。

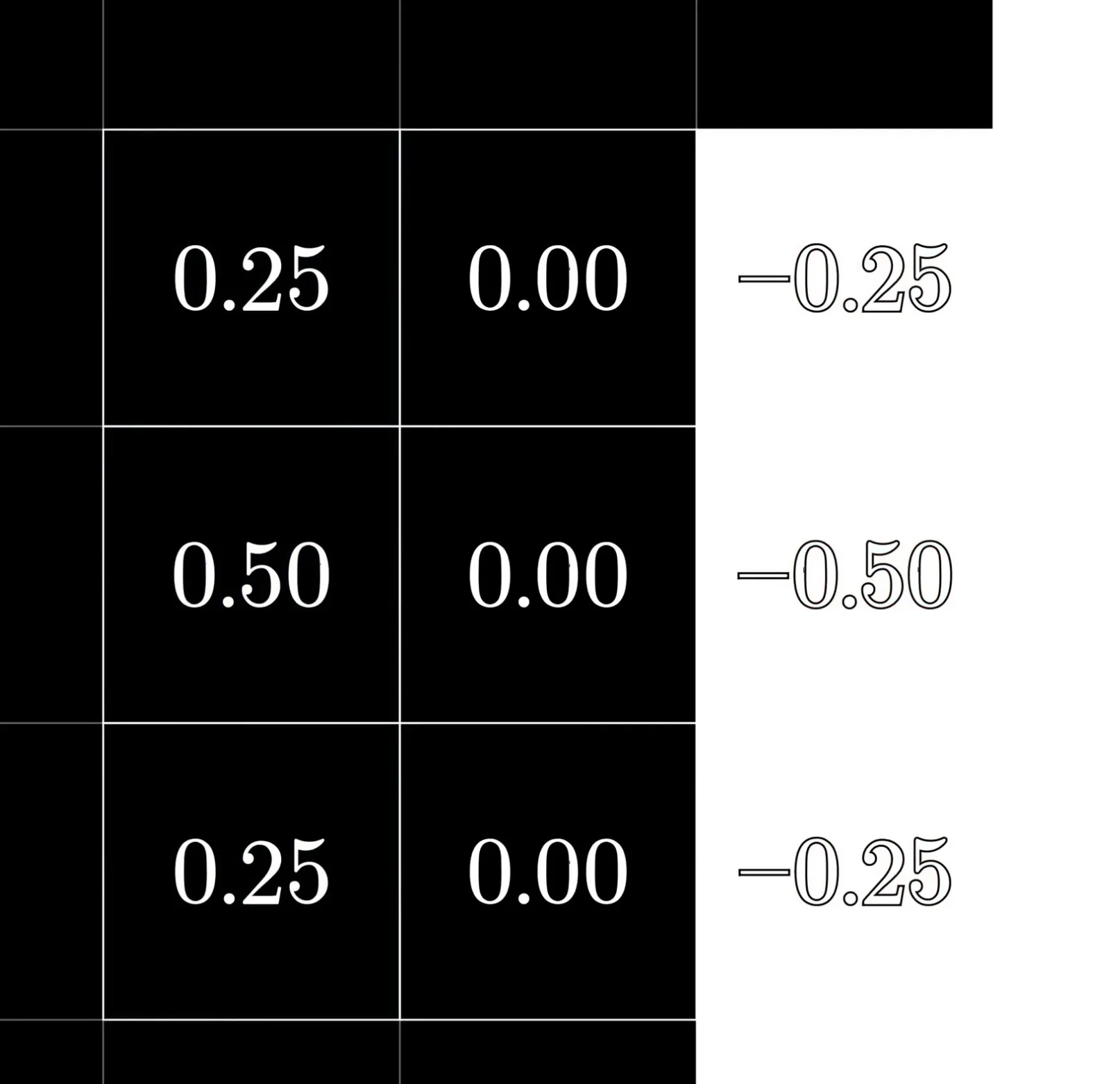
比如图中白色的部分会和第三列内积，黑色部分和左边两列内积

如果我们将这个卷积核翻转一下，他就可以识别图像的横向边界

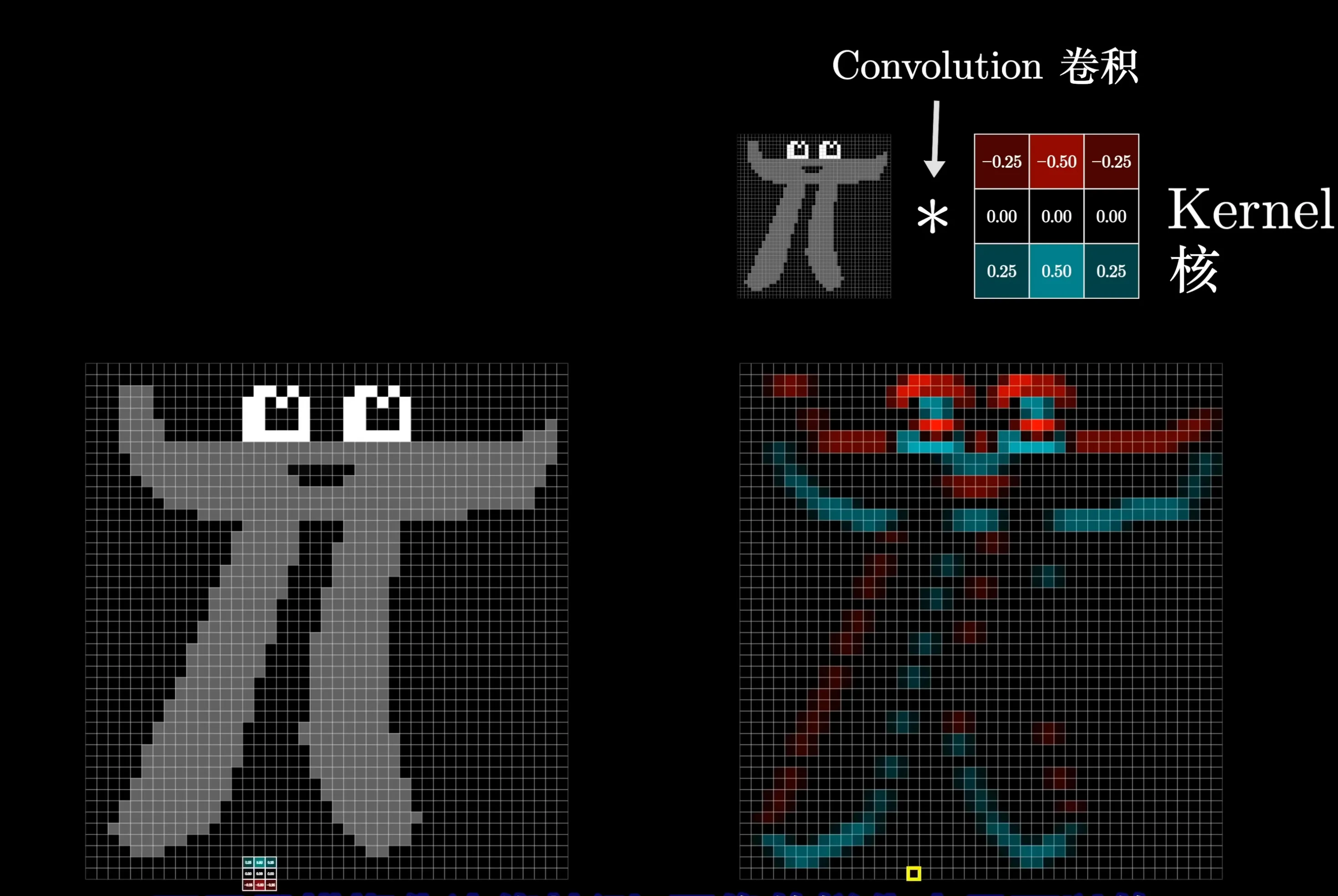
如果我们将这两种卷积核操作过后的结果结合一下，我们就可以得到整个图像的轮廓。

事实上，在神经网络的训练中我们并不设定这个卷积核应该提取什么特征，而是经过损失函数评判，反向梯度传播之后，我们不断调整卷积核里面的参数。卷积核的学习过程，就是在训练中“变形自己”，最终变成一个“对目标任务最有帮助的特征检测器”。每一层都在提取更抽象、更有用的图像特征。

卷积的含义#

deeplearning中的filter为什么要叫卷积，要知道这可不是数学定义上的卷积，称之为卷积的原因是他在本质上和数学的卷积有点类似。在本质上，无论是概率论还是深度学习中，卷积都是在做一个“滑动+相乘+求和”的操作。deeplearning中的卷积是一种离散型的卷积。

在概率论中我们定义的卷积是想要知道两个随机变量加和之后的分布，假设现在有连续型随机变量X和Y，他们之间相互独立，他们的然后我想知道x+y=z, z的概率是什么。

$$f_Z(z) =(f * g)(z) = \int_{-\infty}^{\infty} f_X(x) f_Y(z - x) dx$$

我们就可以看作是g函数翻转后平移z个单位之后与f函数相乘再相加的结果，当我们改变x的取值的时候就相当于“扫/滑动”这个过程。

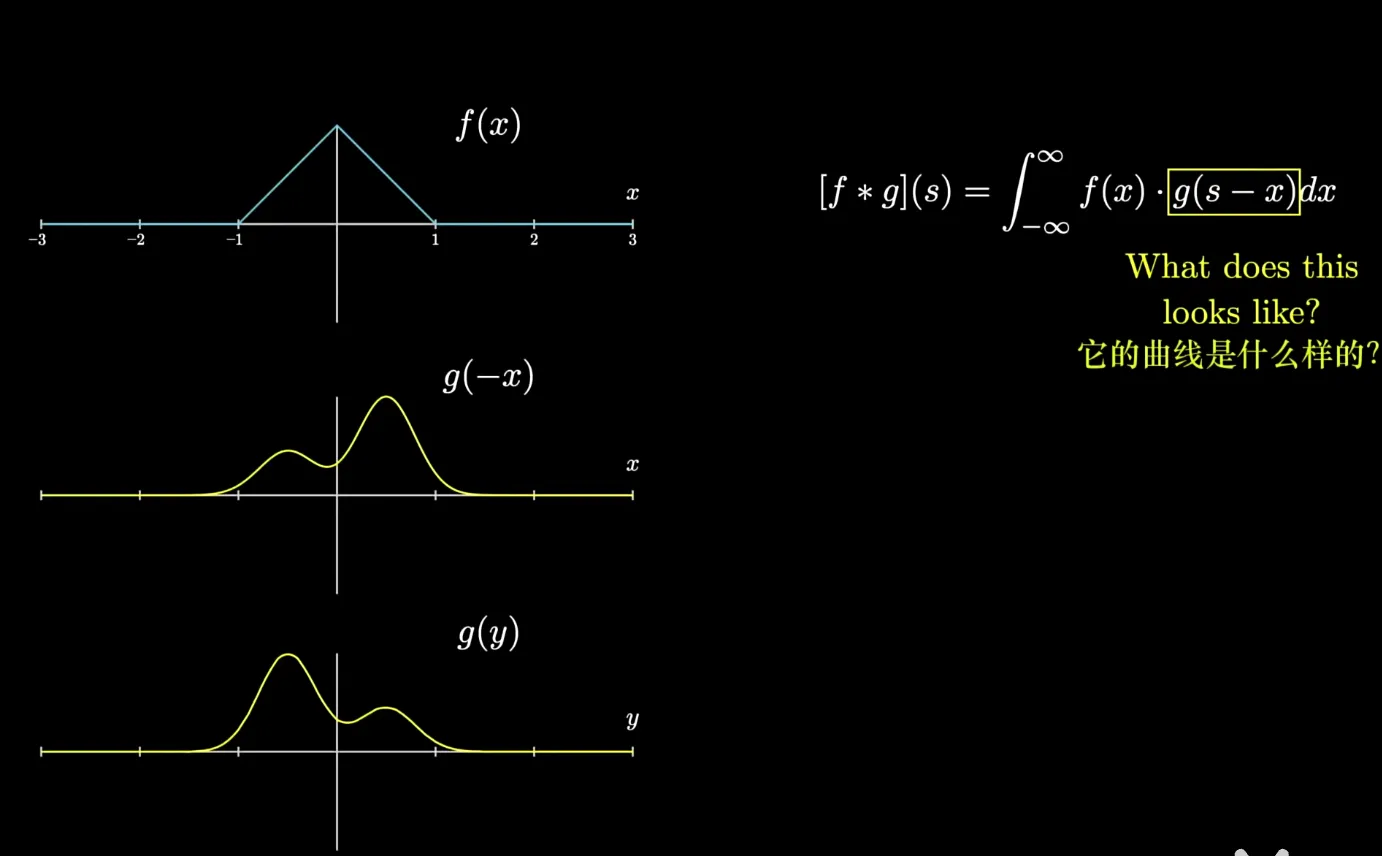
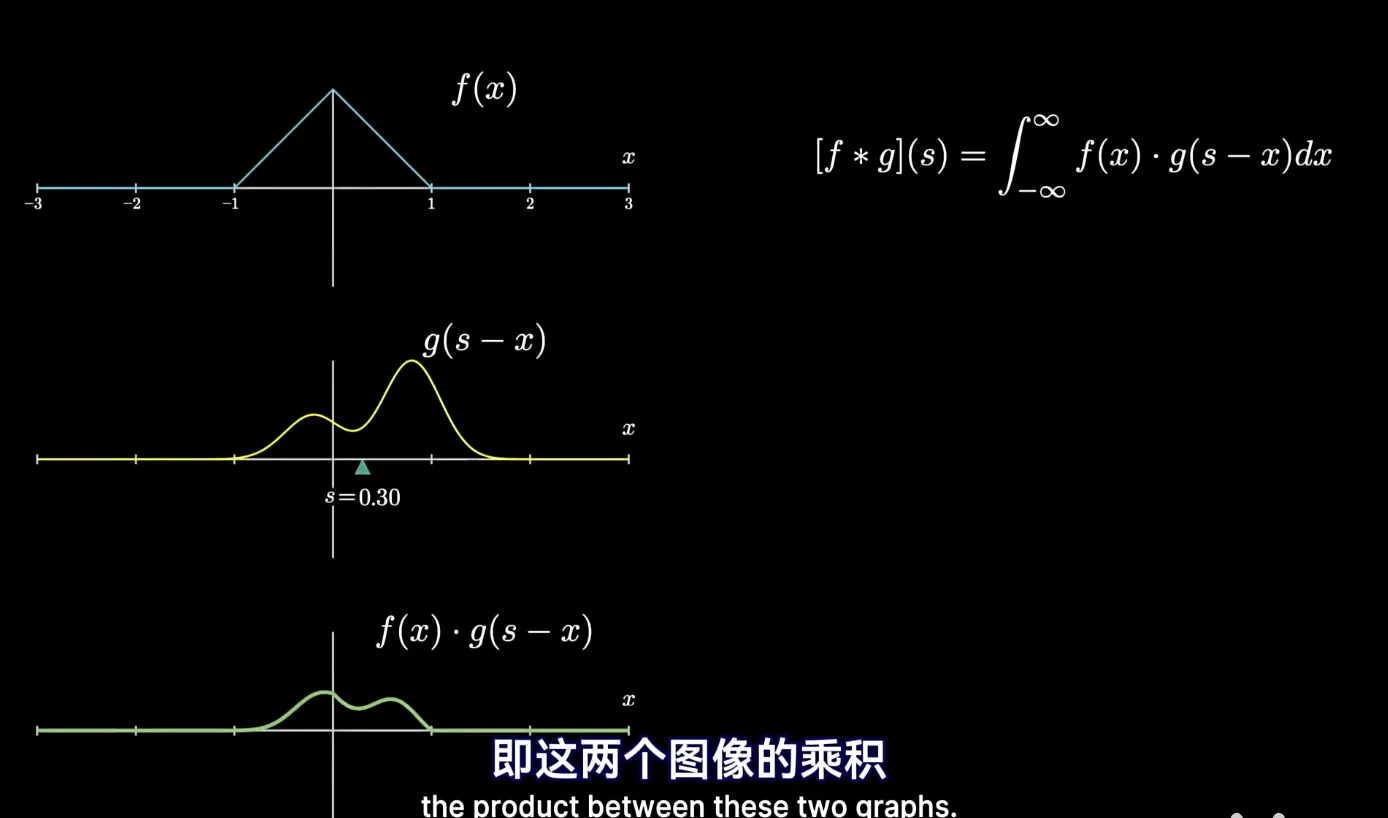
这个卷积的含义还可以有别的方式理解，这里主要想讲一下deeplearning中的卷积和概率论中的卷积中的相似之处，更深刻的理解概率论中的卷积可以参考3Blue1Brown的视频 ↗，以及他的离散型卷积的理解 ↗ 讲的非常生动。