论文笔记

Authors: “Weixing Xie, Junfeng Yao, Xianpeng Cao, Qiqin Lin, Zerui Tang, Xiao Dong, Xiaohu Guo”

Date: ‘2024-01-01’

URL: “https://link.springer.com/10.1007/978-3-031-72089-5_58 ↗”

对内窥镜视频的动态重建（Dynamic reconstruction）对于机器人手术是关键的。动态重建的目的比如能用2D的视频重建出3D场景，然后投影到2D，可以为医生提供别的视角而不只是摄像头的单一视角，以及将可以将手术仪器这些移除，以此看到被手术仪器遮挡的部分。

之前的重建技术都是基于NeRFs，虽然取得不错的成绩但是这种技术不能处理一些细节并且不能实时渲染，不止如此，受限制的单视感感知和遮挡仪器还提出了手术现场重建的特殊挑战。所以本篇论文就介绍了他们的基于3D Gaussian的新技术叫SurgicalGaussian，最终的效果就是能够去除视频中的手术工具，并且能有一个高质量的渲染，以及更快的渲染速度和GPU利用率。

Introduction#

一开始介绍了一下3维重建的历史，手术场景的3维重建的重要性

然后一开始人们基于 point clouds and surfels（点云和表面元素）对手术场景进行离散的建模，但这种技术不能够处理剧烈运动和拓扑变化引起的颜色改变问题，比如角度不同，导致光照不同，最终导致颜色发生变化。

然后NeRF技术就产生，相比于点云，这个方法用的是连续表示场景，这种方法在生成高质量的外观和几何图形方面具有优势。然后EndoNeRF改进了NeRF，EndoNeRF相比于NeRF引入depth suervision(深度监督)。同时还有LerPlane这个技术，他对采样点的时空特征进行了有效编码，减少了动态组织建模的工作量。但是基于NeRF的这些方式需要消耗大量的计算资源，很难进行实时渲染。

所以就有了3D Gaussian Splatting (3DGS)，他能产生逼真的渲染效果，同时训练速度也比NeRF快。具体来说，这个方法就是将场景用三维高斯来表示，并且用可变光栅管道来渲染图像。

本篇的在3DGS的基础上进行了一些改进：

他们提出了deformable 3D Gaussians framework （可形变三维高斯框架）
有效的高斯初始化策略（GIDM）
通过颜色正则化和形变正则化，分别解决了遮挡区域的颜色预测和高斯形变场的噪声问题。
高质量的重建质量和实时渲染速度

Method#

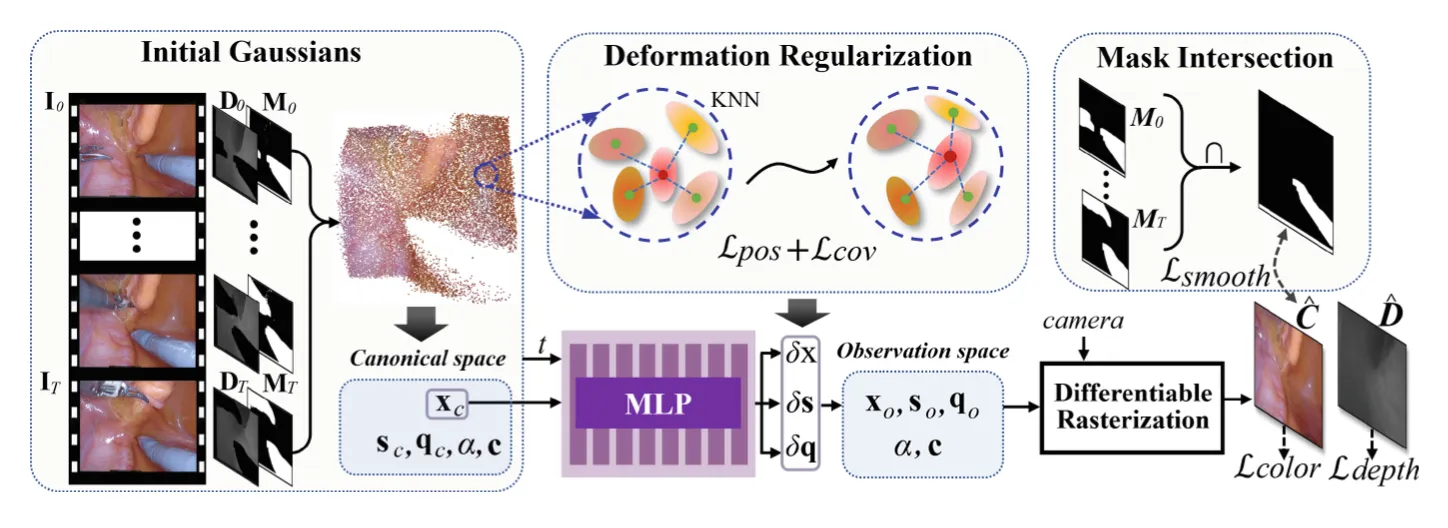
将视频作为输入, $V = {I_i,D_i,M_i:i∈[0,T]}$ , $I_i$ 表示第i帧的图像， $D_i$ 是深度图（Depth Map），用于表示图像中每个像素点到摄像机的距离。 $M_i$ 表示mask，用1来表示图中手术工具的部分，其他用0表示。给定这些输入，能构产生可以去除手术器械并以高质量恢复变形的软组织的场景

Preliminaries(前言)#

本质上3DGS的方法就是输入一组图片（视频帧），根据这些图片，训练一个模型使之能够根据这些构建一个3D的场景，这个场景就是一个3D 高斯点云，然后根据这个3D场景，我们可以选择不同的视角，然后将这些点投影到对应视角的2D图像上。

每一个3D高斯点我们就表示为Gaussian primitives $\mathcal{G}$ （高斯基本单元）这不是一个无结构的单点，而是一个 椭球形的 3D 形状，由协方差矩阵 Σ 控制其方向和大小。当我们从某个视角观察一个 3D 场景时，每个高斯分布会投影到 2D 屏幕上，形成一个 高斯形状的斑点（splat），类似于散景模糊的点。
渲染时，所有这些 2D 高斯点会叠加在一起，形成最终的 2D 图像。 $G(x)=exp(−\frac{1}{2}(x−μ)^TΣ^{−1}(x−μ))$

这里的 Σ 为协方差矩阵，他控制高斯的形状和方向，向量 $x\in R^3$ 表示世界坐标系中的点，这里默认的高斯中心μ为0，其中其中 $Σ=RSS^TR^T$ ，S是缩放矩阵，R是旋转矩阵。

然后文章中只用向量 $s\in R^3$ 来记录S的对角线元素，这个向量表示沿着 x、y 和 z 轴的缩放因子。 $q\in R^4$ 记录旋转矩阵的四元数,以此不用记录整个矩阵从而节省空间

每一个高斯点还需要 $\alpha$ 表示透明度，c表示球面调和函数系数（Spherical Harmonics Coefficients）用于存储和计算球面上的光照或颜色分布

因此高斯基本单元就可以表示为 $\mathcal{G}$ = {(x,s,q, $\alpha$ ,c)}

然后通过视图变换矩阵V：通过视图变换将三维物体的坐标转换到相机坐标系中，这样物体相对于相机的方向和位置就确定了。

投影变换的仿射近似的雅可比矩阵 J来将该视角的3D场景投影到2D中。

然后对于2D图片上每一像素 r 我们可以根据公式得出他的颜色和深度信息

\hat{C}(\mathbf{r}) = \sum_{i} (\alpha_i' \prod_{j=1}^{i-1} (1 - \alpha_j')) c_i,\\ \hat{D}(\mathbf{r}) = \sum_{i} (\alpha_i' \prod_{j=1}^{i-1} (1 - \alpha_j')) d_i. \tag{1}

GIDM Initialization Strategy(GIDM初始化策略)#

当一开始我们训练将2D转化为3D高斯点云的模型的时候，我们需要初始化这些高斯点的参数，通过投影然后和真实场景的2D图像对比，来不断调整这些高斯点的参数。一个好的初始化策略可以加速模型的收敛。

一开始的3DGS用SFM来初始化这些参数，但是对于内窥镜这种复杂多变的场景，他的准确率就不太高。因此提出GIDM初始化策略。

文章中的初始化策略就是帧与帧之间相互补充信息，在别的帧中出现的组织信息就被补充进点云中，最终点云中有的就是所有帧中组织信息的并集，缺失的就是所有帧中mask(手术仪器)的交集，以此来初始化。

公式就是这个

\mathbf{P}^* = \{ \mathbf{D}^* \mathbf{K}_e^{-1} \mathbf{K}_i^{-1} (\mathbf{I}^* \odot (\mathbf{1} - \mathbf{M}^*)) \}, \mathbf{M}^* = \bigcap_{i=0}^T \mathbf{M}_i. \tag{2}

$P^∗$ : 这是生成的点云的集合，每个点是空间中的一个三维点。
$D^∗$ : 这是深度图（depth map）中的深度信息，表示相机与场景中每个点之间的距离（深度值）。
$K_e$ : 这是相机的外参矩阵（extrinsic matrix），通常用于描述相机在世界坐标系中的位置和朝向。它描述了相机的旋转和平移变换。
$K_i$ : 这是相机的内参矩阵（intrinsic matrix），描述了相机的焦距、主点、以及像素坐标系与相机坐标系之间的关系。
$I^∗$ : 这是输入的图像或深度图像，表示场景中每个像素的颜色或灰度值。在此上下文中，可能代表场景图像的颜色通道或亮度。
$M^∗$ : 这是一个掩码（mask）图像，用于指示哪些区域有效。掩码通常用于处理图像中的背景或无效区域（例如，深度信息缺失的区域）。
⊙: 这是哈达玛积（Hadamard product），表示逐元素乘法。在此上下文中，它是将图像信息（例如，颜色信息或灰度值）与掩码 $(1−M^∗)$ 相结合，剔除无效区域。

Deformable 3D Gaussian Representation#

当我们处理处理动态场景时，我们将一开始获得的是组织的高斯点云，但是这个点云是静态的，这些点云一开始存储在Canonical Spac（标准空间）中，他不会随着组织发生的形变而产生变化，于是我们就用deformation network（形变场）来建模这些点随时间是怎么运动的，他的的核心作用是：

映射标准空间的高斯点到任意时间步的实际位置，从而使得这些点能随时间变化。
学习物体的运动规律，可以建模简单的刚体运动（Rigid Motion，如平移、旋转），也可以建模复杂的非刚体形变（Non-Rigid Deformation，如人脸表情、衣物摆动等）。

相当于给定时间 t 和高斯点的初始坐标，我们就可以得到t时间对应高斯点的坐标。这种方法在处理多个高斯点的时候非常的灵活，同时还可以节省空间，不用记录下每个高斯点的每个时间的位置。

文章中，他们的这个形变场用的就是MLP来进行建模，将一开始生成的高斯点云输入进去，然后训练的这个MLP，让他预测之后点云的形状，然后再把预测后的点云投影到2D中，和实际的视频帧进行比对，以此来训练。

训练完成后，他就可以输入一个高斯点的坐标 $x_c$ ，和时间 t ，他就可以计算出这个高斯点的偏移。 $(δx,δs,δq) = F_Θ((γ(x_c),γ(t)).$

位置变化 δx
缩放变化 δs
旋转变化 δq
形变场 $F_Θ$
位置编码函数 $γ()$ , 位置编码的作用是：

增强 MLP 的表达能力：如果直接输入坐标 (x,y,z)，MLP 可能难以学习到高频变化的运动。
通过特定频率的编码，让 MLP 学习复杂的运动模式。

然后 t 时间的高斯点就变成 $\mathcal{G_0} = {(x_0,s_0,q_0,\alpha,c)}$ 其中 $x_0 = x_c + δx,s_0 = s_c· exp(δs),q_0 = q_c· δq$

$\alpha,c$ 不变，因为他们是高斯的固有属性。

Optimization#

他们的这个框架同时优化MLP形变场的参数以及2D转成标准空间下的3D高斯点云质量，以及去除手术器械。

\mathcal L_{\text{color}} = \left\| (I_i - \hat{C}_i) \cdot (1 - M_i) \right\|_1

真实彩色图像 $I_i$ 和预测图像 $\hat{C}_i$ 相减，然后取出手术器械部分 $(1-M_i)$ 然后求 L1 范数，就是矩阵的每个数的绝对值加起来，这个公式就是损失函数

\mathcal L_{\text{depth}} = \left\| (D_i - \hat{D}_i) \cdot (1 - M_i) \right\|_1. \tag{5}

和上面式子意思类似，是深度的损失函数

Deformation Regularization.#

在处理单视角时候，形变场会后一些限制，这会造成噪声。于是文章提出一种正则化方法，让一个高斯点附近的高斯点之间有相似的形变。

\mathcal{L}_{pos} = \sum_{i=1}^{N} \sum_{k=1}^{K} \left\| d\left(\mathbf{x}_c^{(i)}, \mathbf{x}_c^{(k)}\right) - d\left(\mathbf{x}_o^{(i)}, \mathbf{x}_o^{(k)}\right) \right\|_1. \tag{6}

位置损失函数 $\mathcal{L}_{pos}$ ，计算标准空间中每个高斯点 i 和他周围K(文章中K=5)个点的的距离，和观察空间中点i和他周围K个点的距离，然后求范数，就得到损失函数

\mathcal{L}_{cov} = \sum_{i=1}^{N} \sum_{k=1}^{K} \left\| d\left( \mathbf{Σ}_c^{(i)}, \mathbf{Σ}_c^{(k)} \right) - d\left( \mathbf{Σ}_o^{(i)}, \mathbf{Σ}_o^{(k)} \right) \right\|_1. \tag{7}

这个是协方差矩阵的损失函数 $\mathcal{L}_{cov}$ ，与上面的公式类似

Occlusion-Based Color Regularization（基于遮挡的色彩正则化）#

因为NeRFs是用连续的办法表示场景，因此可以很好的弥补从头到尾被手术仪器遮挡的部分，但是3DGS是基于离散的高斯点，mask $M^*$ 让这部分的图像缺失，所以在从头到尾被手术仪器遮挡的部分他会使得渲染的图片中有个空洞，于是文章中引入a total variational loss，利用周围的点的颜色可以帮助弥补缺失的那部分颜色。

\mathcal{L}_{smooth} = \frac{1}{n} \sum_{p,q} \left( \| \mathbf{C}^{p,q} - \mathbf{C}^{p-1,q} \|_{2}^{2} + \| \mathbf{C}^{p,q} - \mathbf{C}^{p,q-1} \|_{2}^{2} \right), \mathbf{C} = \hat{\mathbf{C}}_{i} \odot \mathbf{M}^{*}, \tag{8}

这个公式的意思就是比较 (p,q) 位置的像素值和(p-1，q),(p,q-1)位置像素值的差异，用欧几里得范数的平方来度量，求和n个像素之后取平均。

Total Loss#

最后他们再添加3DGS中的SSIM loss 得到最终的损失函数

\mathcal{L} = (\mathcal{L}_{color} + \lambda_1 \mathcal{L}_{ssim} + \lambda_2 \mathcal{L}_{depth}) + (\lambda_3 \mathcal{L}_{pos} + \lambda_4 \mathcal{L}\_{cov} + \lambda_5 \mathcal{L}_{smooth}). \tag{9}

Experiments#

这里就讲了一下他们实验的结果，交代数据集，和其他之前已有的模型进行比较,分析之前方法的缺陷，进行消融实验（Evaluation Metrics）¹，交代他们的实验细节。

Conclusion#

概括了一下他们的创新点，成果，明显好于SOTA²，说本文为手术场景建模提供一种新思路。

消融实验的目的在于移除系统中的特定的部分，来控制变量式的研究这个部分对于系统整体的影响。如果去除这一部分后系统的性能没有太大损失，那么说明这一部分对于整个系统而言并不具有太大的重要性；如果去除之后系统性能明显的下降，则说明这一部分的设计是必不可少的。当然，如果出现了第三种情况，也就是去除之后模型的性能不降反升，那么建议找一下bug或者修改设计。 ↩
SOTA 是 State-of-the-Art 的缩写，表示某一领域当前最先进的方法、技术或结果。它常用于学术论文、机器学习和人工智能研究中，指 在某项任务上性能最优的方法或模型。 ↩