Lecture3 Linear Classifiers • Laurie's Site

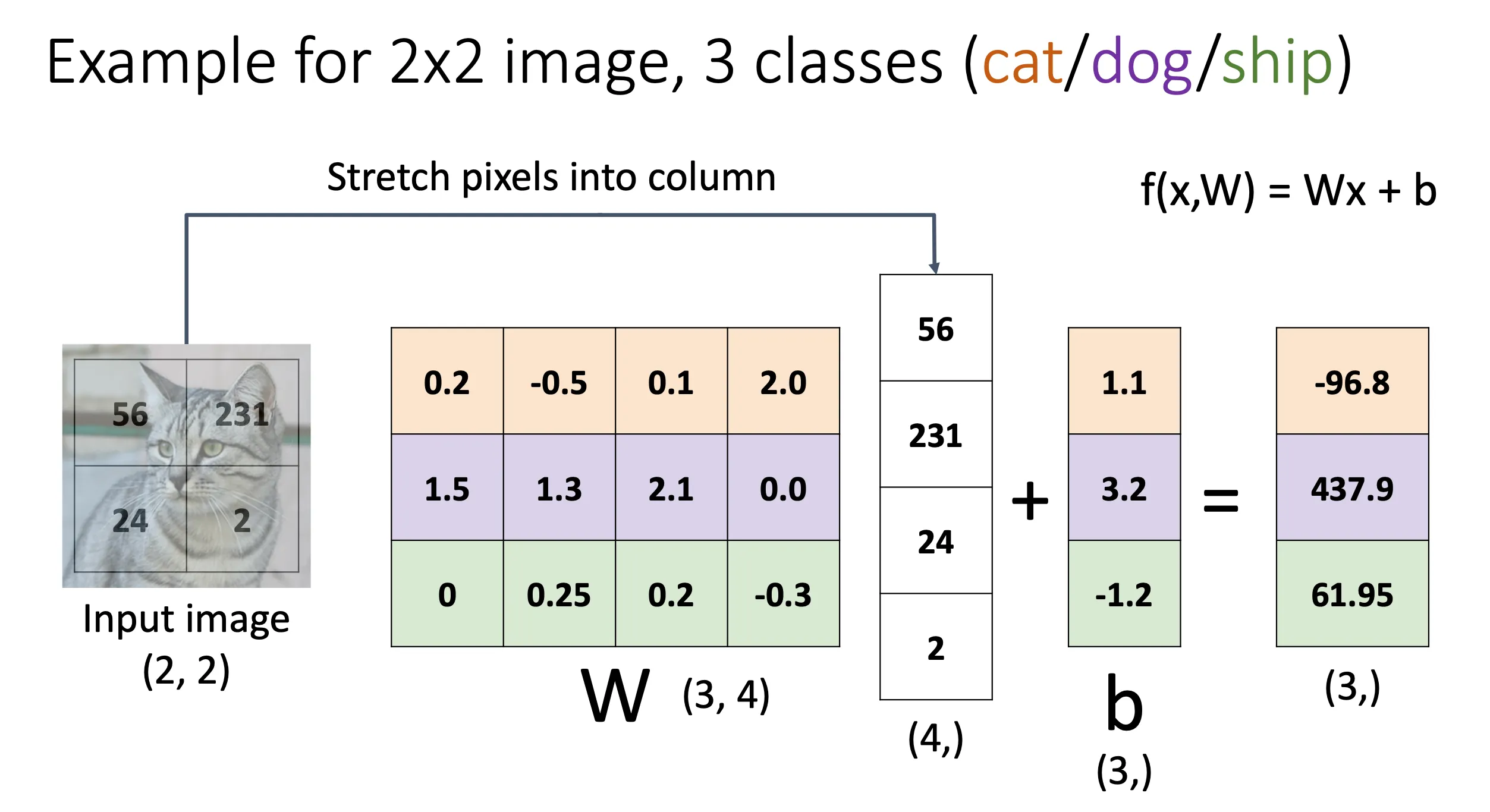
Parametric Approach(参数法)#

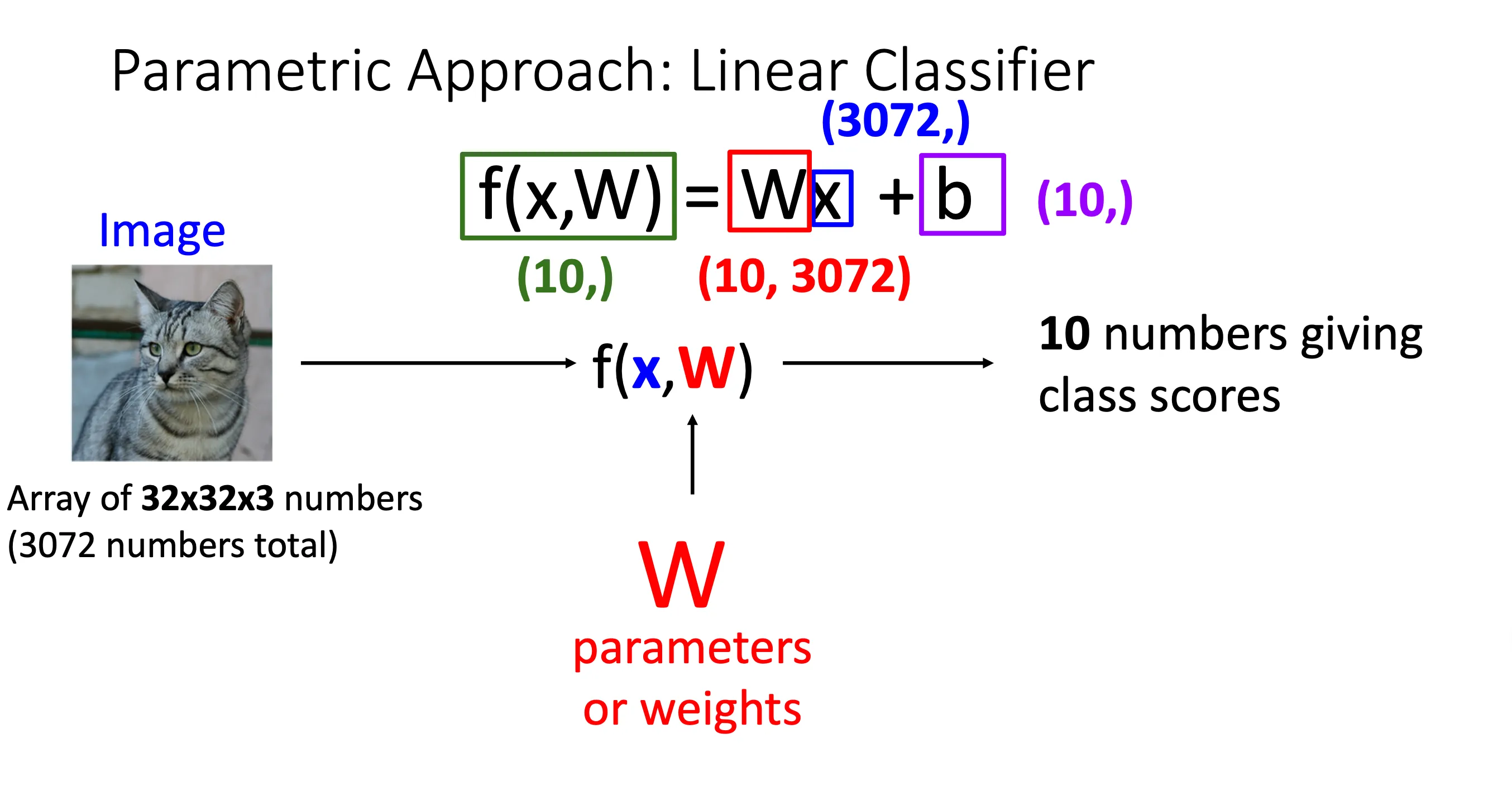
alt text

$f(x,W)=Wx+b$ 这一个的方法就是先根据照片的长宽像素以及RGB 3 bit生成一个一维向量，如图就是 $32\times32\times3=3072$ 的一维向量。然后去乘一个矩阵，这个矩阵的大小是一维向量的大小和想要区分的标签的大小，比如图中就是总共有10个我们想要进行分类的标签，所以矩阵的大小就是 $10\times3072$ 这样的话我们乘出来的结果就是一个 $10\times1$ 的矩阵，这就代表这张图片在这10中标签中的分数情况。我们还可能加一个偏移量矩阵b，来对结果进行调整。

alt text

Algebraic Viewpoint(代数角度理解)#

Bias Trick#

我们可以将b这个偏差合并到W矩阵中，并且在x中多加一个1，得到的结果不变

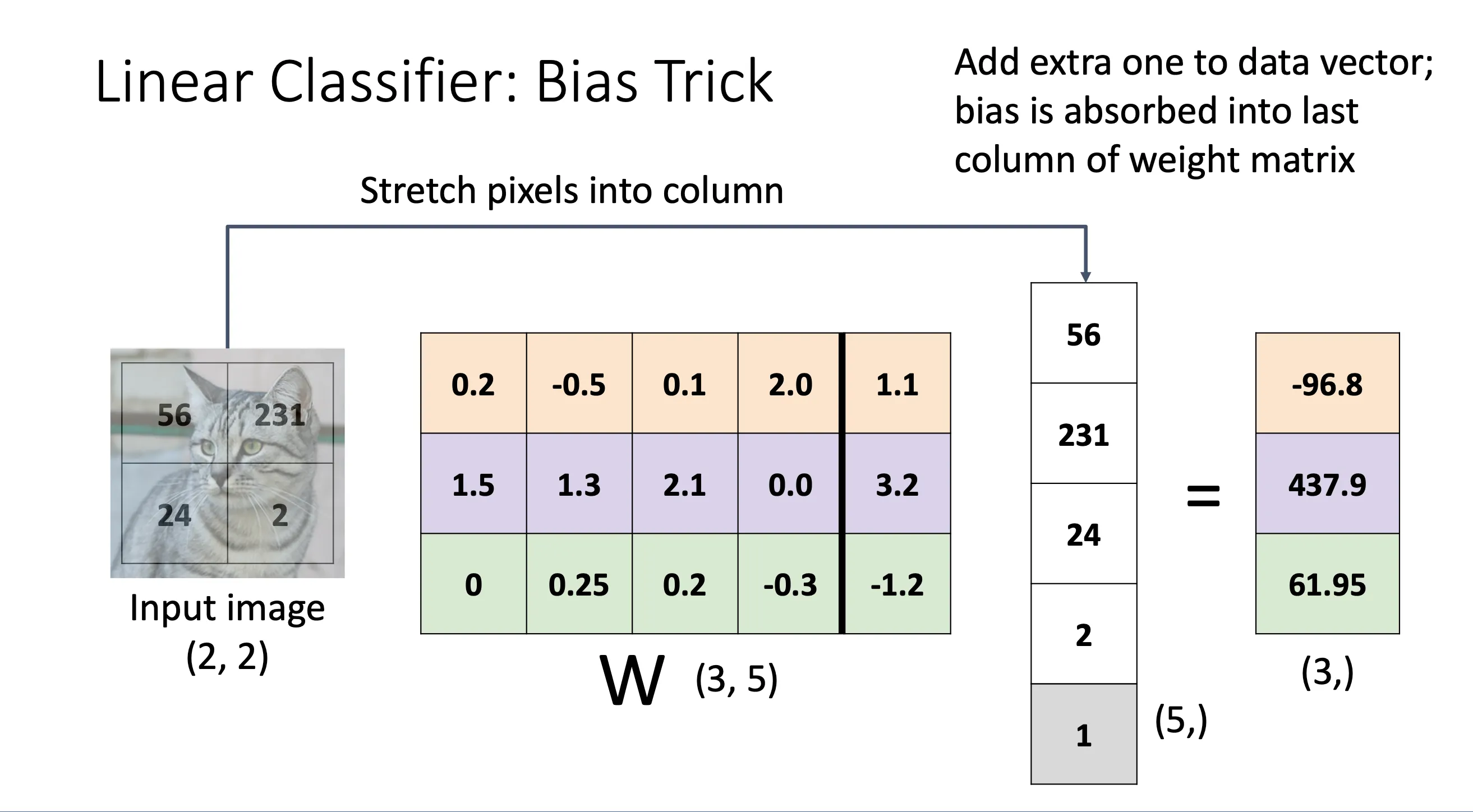alt text 这种做法从代数角度会很有帮助转化后： $f(x′,W′)=W′⋅x′$ 偏置 b 现在就是扩展权重的一部分，代数形式统一为点积运算。

每一个像素乘0.5

Visual Viewpoint#

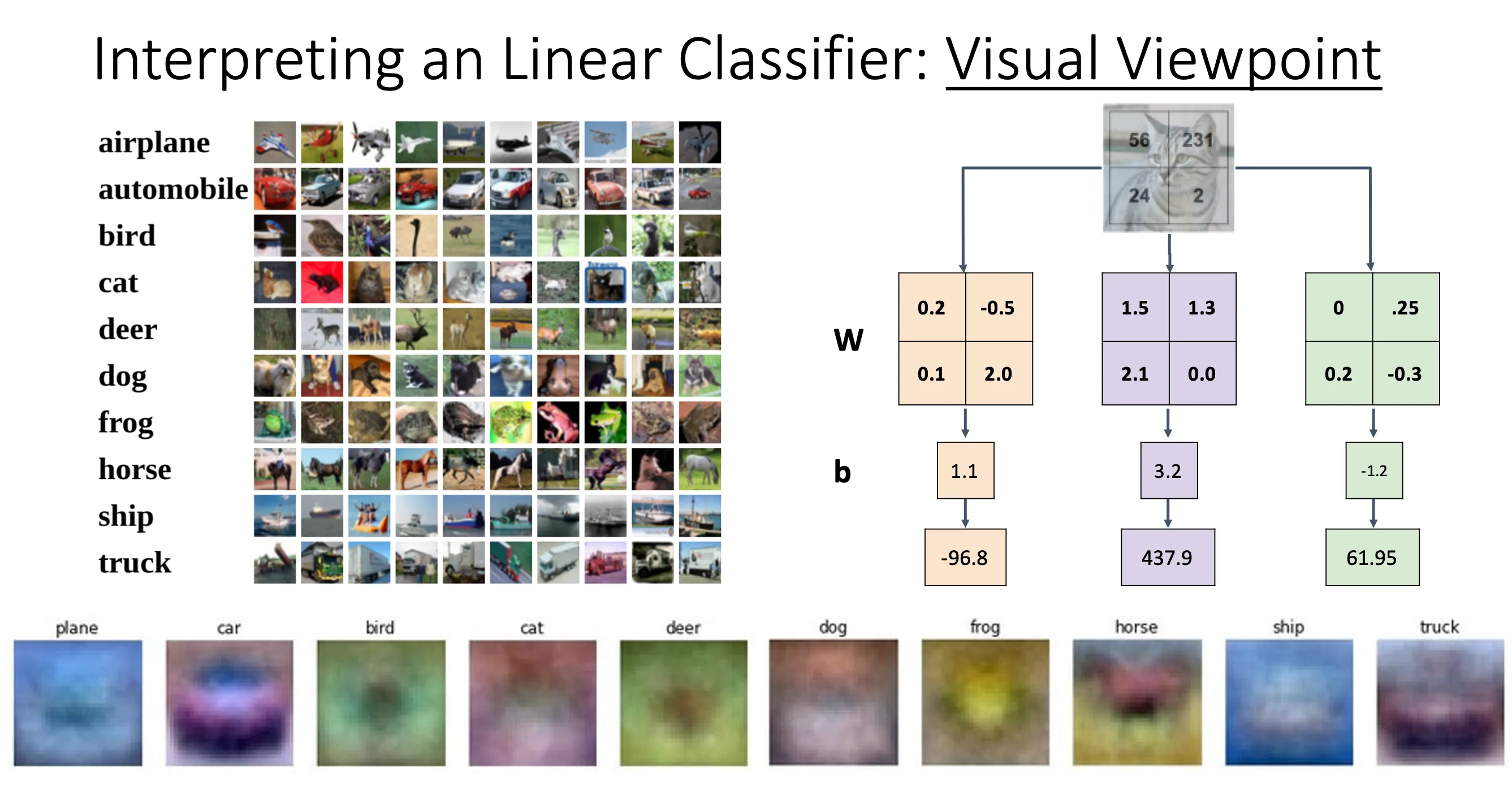alt text 我们不再将图片拆成一维向量，而是将矩阵W拆成图片的形状，这样子可以直接得出每一个标签相应的分数。这种做法有点像拿着不同标签的模版来比对（template matching），每一个标签都有一个模版，根据模版的矩阵内积来评价这张图片的分数

但是从这样的角度我们就可以看到Linear Classifiers的局限性，比如我们要识别一张在森林里面的图片，更有可能的是Linear Classifiers会很大可能将这个识别为deer因为同样背景都有很多绿色，然后car因为中间都差不多有车的模样。以及他特别依赖训练集，比如我们可以看到我们用很多红色的车来训练，所以他的模版就是红色的。但是这样一来当我们有一辆绿色的车之类的他就识别不出来。

还有就是就是A single template cannot capture multiple modes of the data，比如上图中的马看上去有两个头，这是因为当我们训练的时候，有朝向左边的马也有朝向右边的马，这些图片最终会合成一个模版（因为每一个标签只有一个模版），所以我们用一个模版来表示的话就会造成这种两头马。本质上来说就是Linear Classifiers试图用一张图片来涵盖训练集中所有的特征。

Geometric Viewpoint#

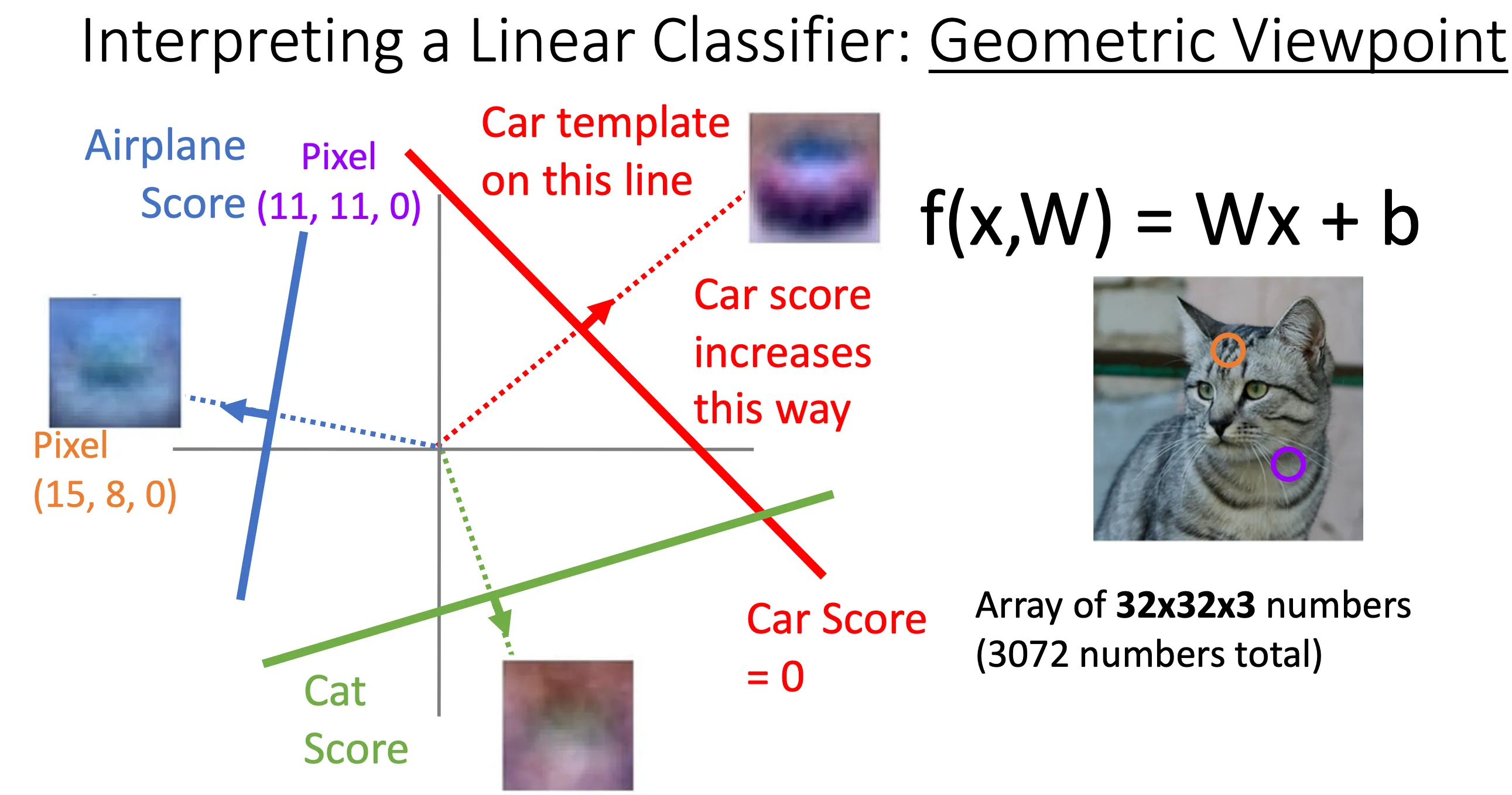alt text 这个角度就是先从图上抽两个像素点，他们的值作为x，y轴，当其他像素点的值保持不动的时候改变他们的值，然后在三维空间中形成一个面，z轴就是对应的分数。

W矩阵中的每一行就对应了一个面，也就对应一个模版，将整个图片和这一行相乘就得到这张图片对应的这个模版的分数。那么就是说W中有多少行（想要识别的标签），他就有多少个平面。一个好的W就应该一个图片在相关的标签的分数应该要比别的模版高。

然后图中的这些线就是面与x，y平面的交线，表示对应的分数为0，然后数学上来看的话就是垂直这条线的话，分数就会增长，前面讲的模版的话就是这个正交线，~~但是分数不一定沿着图中的箭头方向增长吧。有可能延相反方向增长？起点也不一定在原点？~~

然后如果我们将2个像素拓展到整个图像，那应该就是超维的一个平面。从这个观点看，超平面就会将空间切开。

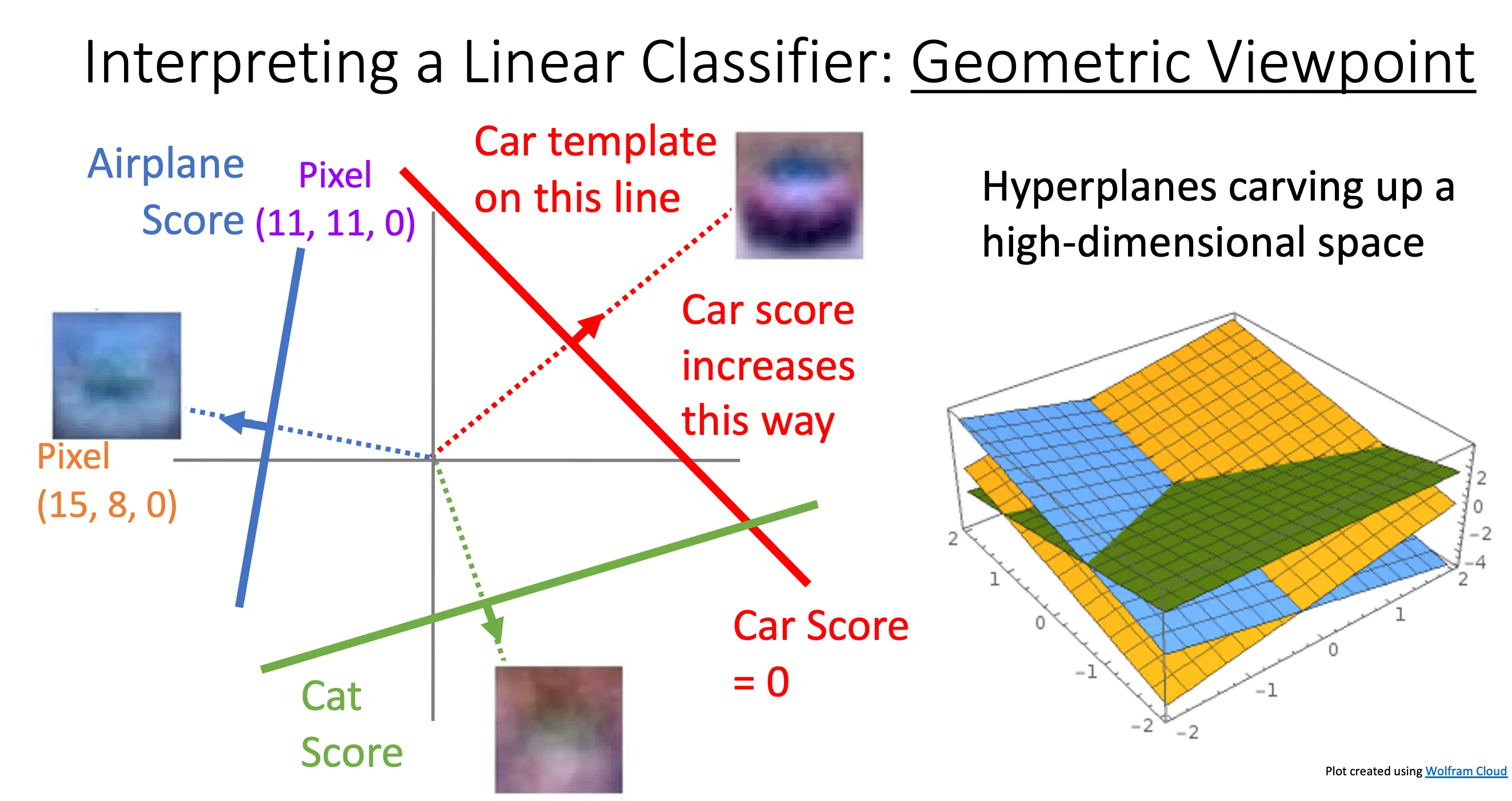alt text 这种方法就会暴露一个问题，linear classifier不能将这些图像通过一个线性的超平面将这些颜色分开来。比如说图中的蓝色部分经过蓝色模版的计算他的分数要比红色的要高，那么就意味着蓝色平面在蓝色部分要比红色平面要高，但在三维中无论平面怎么排列，都可能模拟出下图，因为这只是线性的。

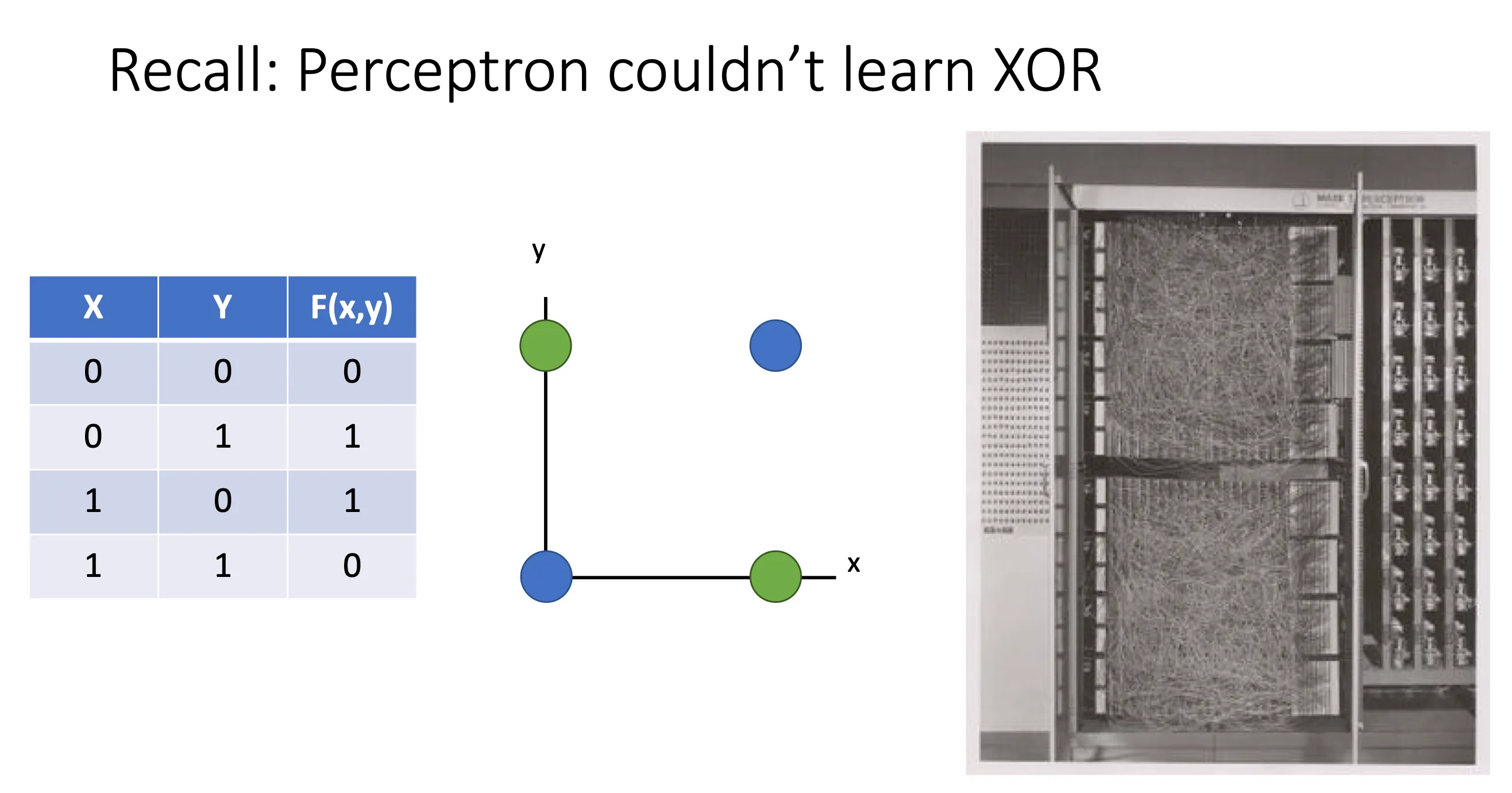
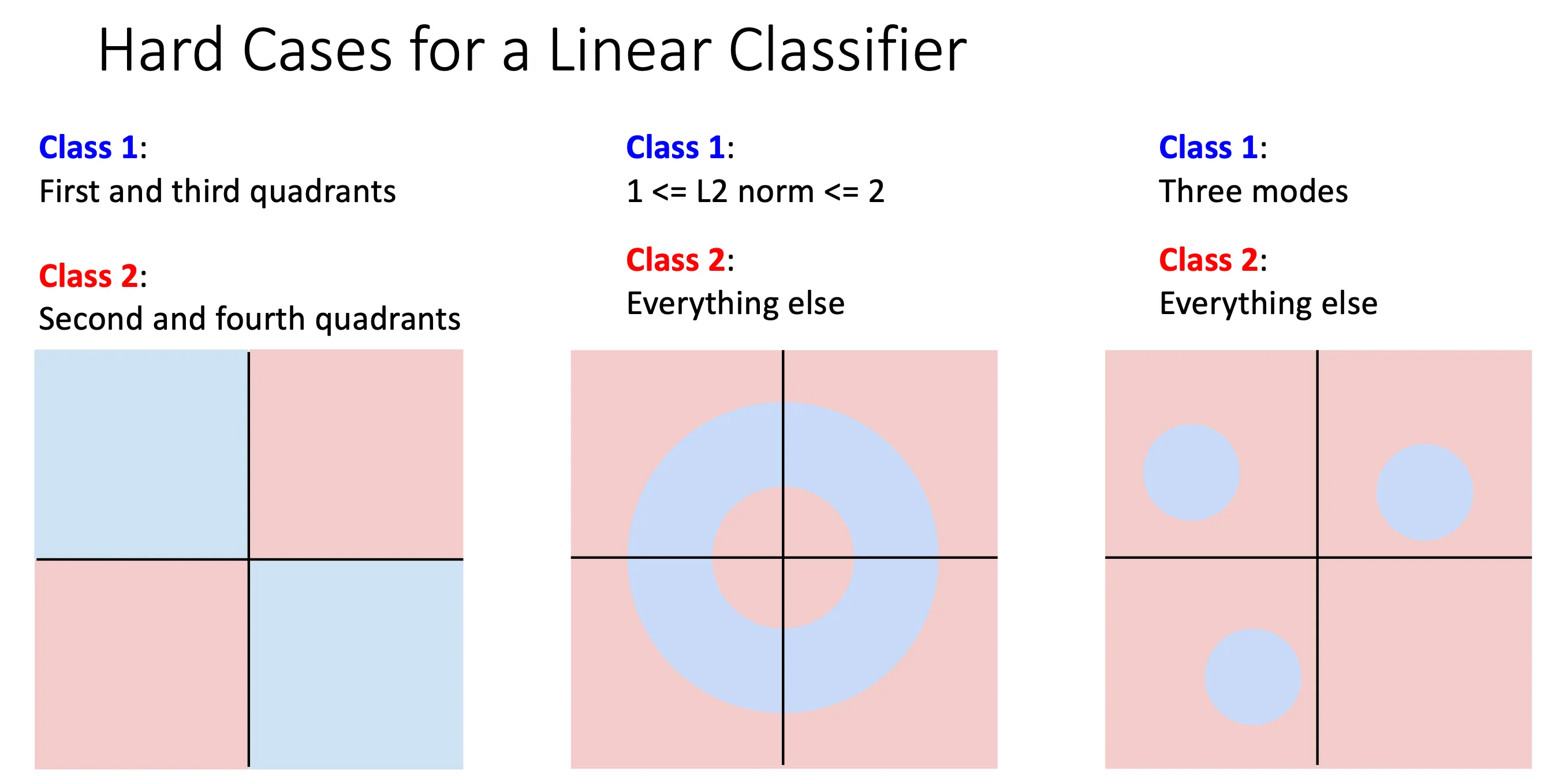alt text 这就是一开始感知机不行的原因，他一开始就是Linear Classifiers，他就连XOR都不能识别

alt text

Choosing a good W#

现在我们的目的就是怎么找到一个合适的W，方法

Use a loss function to quantify how good a value of W is
Find a W that minimizes the loss function(optimization)

Loss Function(损失函数)#

A loss function tells how good our current classifier is Low loss = good classifier High loss = bad classifier

一个数据集可以表示成这样：x表示一张图片，y表示对应标签的index $\{(x_i,y_i)\}^N_{i=1}$

那么一个损失函数通常表示成这样，f表示对于x他经过和W运算之后得到的分数 $L_i(f(x_i,W),y_i)$

平均之后就是 $L=\frac{1}{N} \sum_i L_i(f(x_i,W),y_i)$

Multiclass SVM Loss（多类别 SVM 损失）#

属于一种损失函数

alt text 根据每一个图片用W算出他的分数，如果他正确的标签得分最高，那么他的损失就是0，反之就是算差值。

alt text 假如我们得出了一个W，让他的L为0，意味着这个W可以很好的区分对应的标签，那这个W是否是唯一的呢？很明显不是，因为2W也是0，那么这时候我们就要有一个机制来判断哪一个W更好呢这时就用到正则化

Regularization#

alt text 第二部分（右侧）： λR(W)

这是正则化项（Regularization Term），用于防止模型过拟合。
λ 是一个超参数（hyperparameter），用于控制正则化的强度。较大的 λ 会增加正则化的影响，使模型更简单，较小的 λ 则更关注拟合数据。
R(W) 是对模型参数 W 施加的限制（如 L1/L2 正则化）。

正则化的目的

Express preferences in among models beyond “minimize training error”(增加一些偏好比如L1正则化注重某一个参数比重，L2注重所有参数的作用)
Avoid overfitting: Prefer simple models that generalize better（避免过拟合化）
Improve optimization by adding curvature

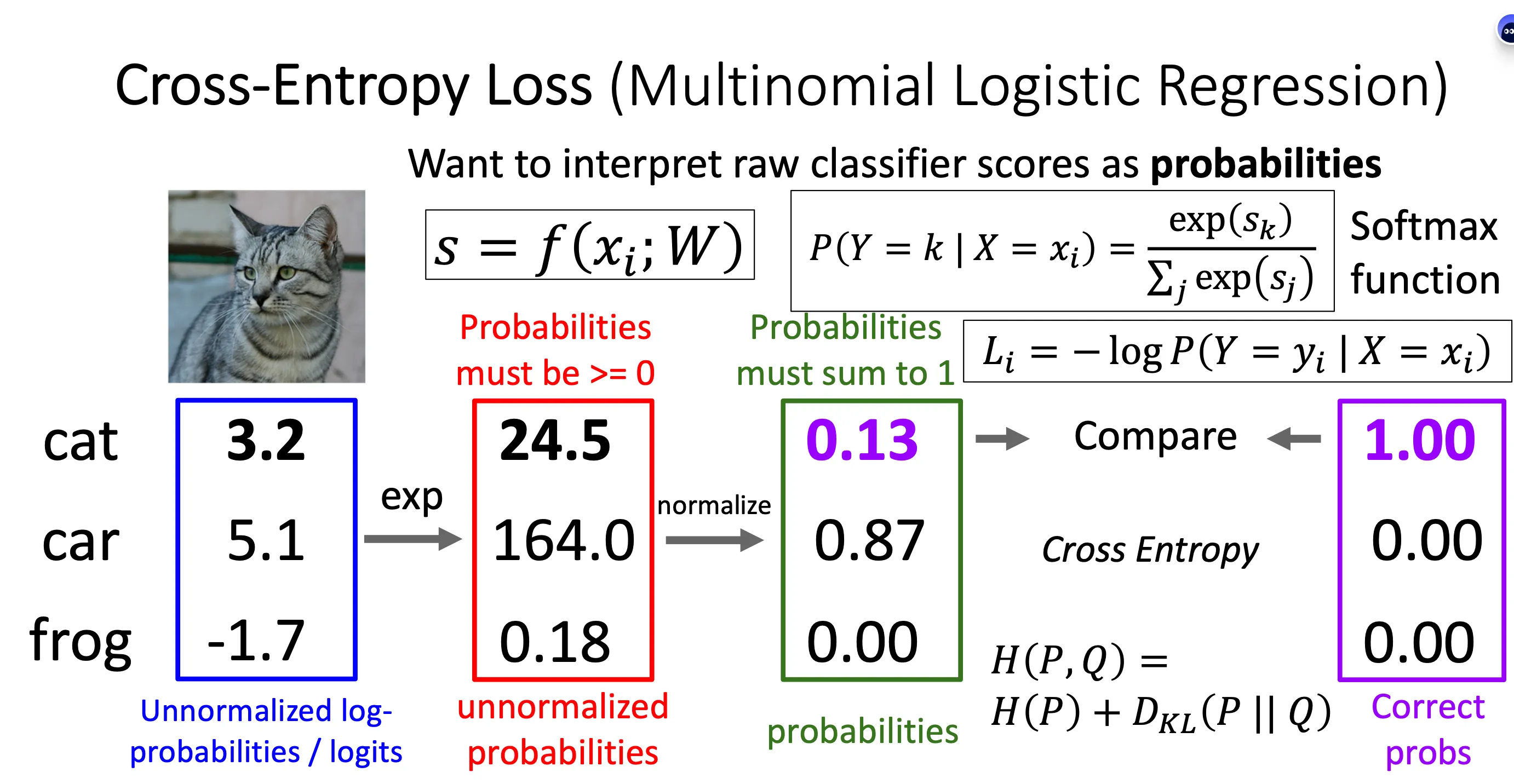
Cross-Entropy Loss (Multinomial Logistic Regression)（交叉熵损失）#

这一个办法就是将分数转化成概率

$分数：s=f(x_i,W)$ softmax公式就是将分数进行用e进行指数化，然后再归一，这样可以避免负数的影响

$Softmax function 归一化：P(Y=k|X=x_i)=\frac{exp(s_k)}{\sum_jexp(s_j)}$

$计算损失：L_i=-logP(Y=y_i|X=x_i)$

Kullback–Leibler（KL）散度是一种衡量两个概率分布之间的差异的方法，常用于信息论和机器学习。它可以理解为“当我们用分布 Q 近似真实分布 P 时，Q 造成了多少信息损失”。 KL 散度（DKLDKL）的计算公式如下： $D_{KL}(P∣∣Q)=∑_yP(y)log⁡\frac {P(y)}{Q(y)}$ 其中：

P(y)P(y) 是真实的概率分布（ground truth）。
Q(y)Q(y) 是我们希望学习的概率分布（模型的预测概率）。
该公式的核心思想是计算P 和 Q 之间的相对熵。

alt text