Lecture4 Optimization • Laurie's Site

事实上，损失函数只是告诉你当前的W造成的损失是多少，判断这个W到底好不好，但是没有告诉你怎么找这个W。

所以这时候就用到optimization $w^*$ 就是最优的w， $\arg \min_w$ 表示对于 $w$ 的所有可能取值，找到使得 $L(w)$ 最小化的 $w$

$w^* = \arg \min_w L(w)$

optimization method#

random search#

随便选W

follow the slope#

找梯度，沿着梯度下降的地方

Numeric gradient(数值梯度)#

一种是像这样对W的每一个元素都增加一个微小量，保持其他元素不变，然后计算斜率。但是这种办法非常的慢对每个元素都要，实际中W可以非常大同时这种做法只能得到近似，因为我们用的有限的差值来计算

alt text

Analytic gradient(解析梯度)#

更有效的办法就是直接用损失函数来找到他对应的梯度通过莱布尼茨，牛顿的那些数学办法找到梯度具体实现中我们用的是反向传播算法

Gradient Descent(梯度下降)#

Vanilla gradient descent#

$损失函数：L(W) = \frac{1}{N} \sum_{i=1}^{N} L_i(x_i, y_i, W) + \lambda R(W)$

$损失函数梯度：\nabla_W L(W) = \frac{1}{N} \sum_{i=1}^{N} \nabla_W L_i(x_i, y_i, W) + \lambda \nabla_W R(W)$

# Vanilla gradient decsent
w = initialize_weights()   #初始化一个w
for t in range(num_steps): #进行num_steps之后结束
  dw = compute_gradient(loss_fn,data,w) #计算dw
  w -= learing_rate * dw   #每次通过dw对w进行调整，learing rate决定调整速度

python

Hyperparameters:

Weight initialization method
Number of steps
Learning rate

alt text

Batch gradient descent—>Stochastic Gradient Descent（SGD）#

对于Vanilla gradient descent而言，我们需要每次对样本集中的每个样本进行计算，从而得到dw，然而当样本集数量很大的时候，计算的速度就会比较慢。于是，就有Stochastic Gradient Descent

$L(W) = \mathbb{E}_{(x, y) \sim p_{\text{data}}} \left[ L(x, y, W)\right] + \lambda R(W) \approx \frac{1}{N} \sum_{i=1}^{N} L_i(x_i, y_i, W) + \lambda R(W)$

$\nabla_W L(W) = \nabla_W \mathbb{E}_{(x, y) \sim p_{\text{data}}} \left[ L(x, y, W) \right] + \lambda \nabla_W R(W) \approx \frac{1}{N} \sum_{i=1}^{N} \nabla_W L_i(x_i, y_i, W) + \lambda \nabla_W R(W)$

# Stochastic Gradient Descent
w = initialize_weights()   #初始化一个w
for t in range(num_steps): #进行num_steps之后结束
  minibatch = sample_data(data,batch_size)  #选取一部份的样本
  dw = compute_gradient(loss_fn,minidata,w) #根据这一小部份样本计算dw
  w -= learing_rate * dw   #每次通过dw对w进行调整，learing rate决定调整速度

python

Hyperparameters:

Weight initialization method
Number of steps
Learning rate
Batch size
Data sampling

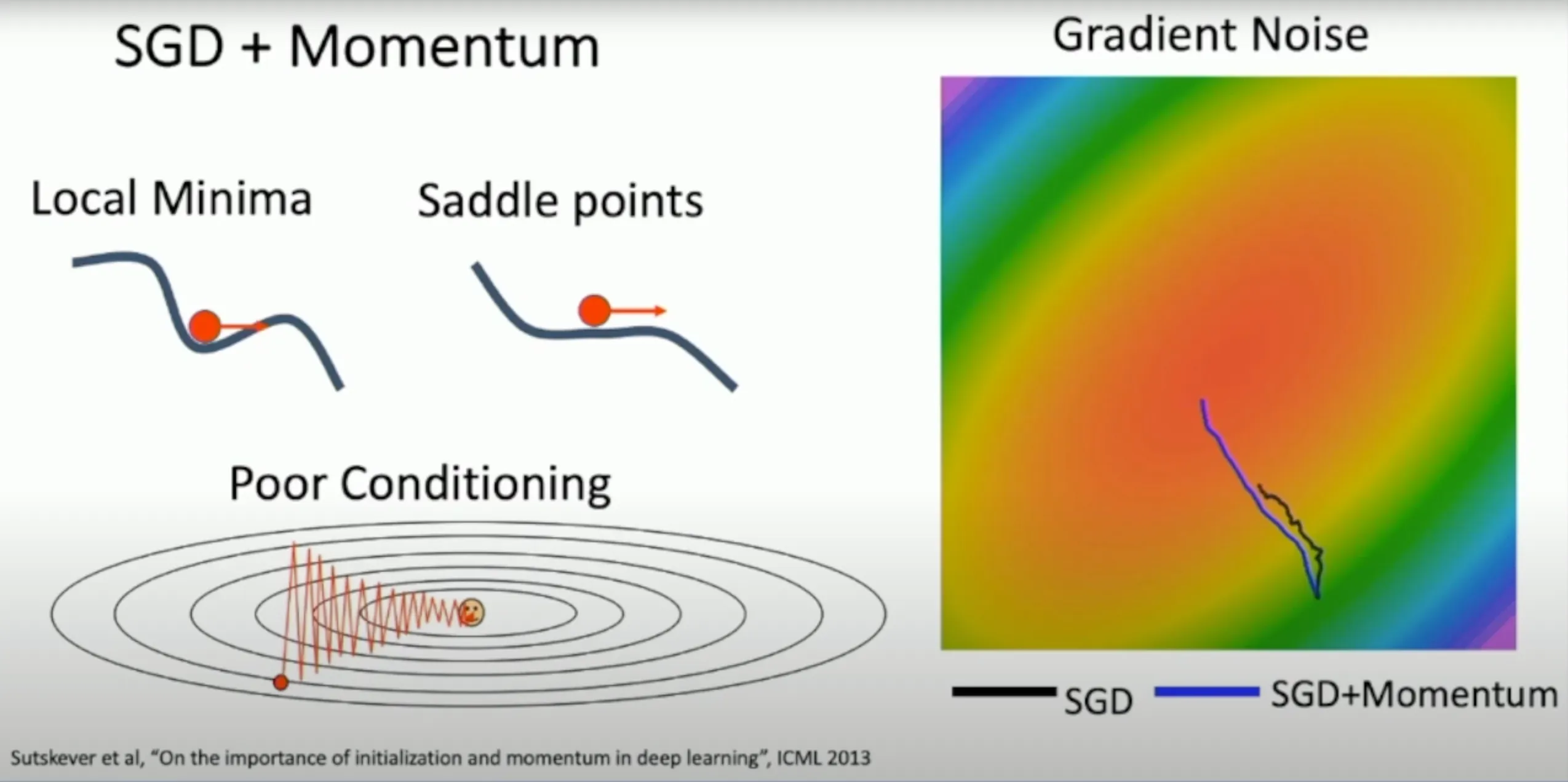
Problems#

如果我们调整的步子太大，我们可能会得到锯齿状的路线，如果过小，可能w收敛的速度会比较慢

alt text

我们会掉入到局部极小值以及鞍点中，而不是全局最小值
对于SGD而言他比较容易受到噪声干扰，因为他只是选取一部份的样本

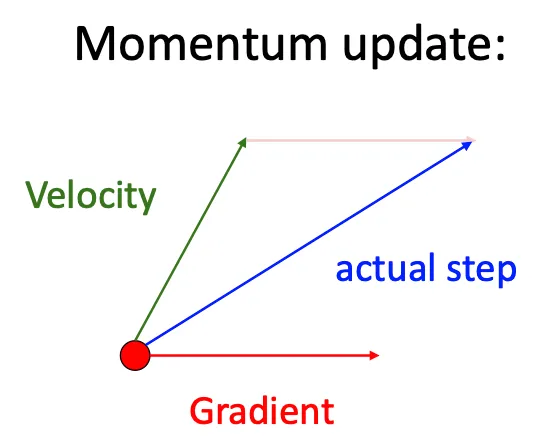
alt text

SGD+Momentum#

v = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  v = rho * v + dw       #他引入了历史的梯度影响，而不只是受到当前梯度的影响
  w -= learing_rate * v

python

这种办法就可以解决上面提到的问题

由于受到历史梯度所以类似于小球掉入局部极小值之后仍有力将他拉出去
受到历史梯度的影响，很明显就可以得出他一定会减缓震荡的幅度
由于受到历史梯度的影响，他就不再会过于敏感与噪声

alt text

这种想法就类似于下图

alt text

AdaGrad & RMSProp#

grad_squared = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  grad_squared += dw * dw
  w -= learing_rate * dw / (grad_squared.sqrt() + 1e-7)

python

每个参数都有一个独立的学习率（learing_rate），这个学习率是通过该参数的梯度历史自动调整的。具体来说，历史上梯度较大的参数会有较小的学习率，而梯度较小的参数会有较大的学习率。
这种调整机制确保了在训练过程中，参数更新较多的方向会逐渐减小学习率，避免过度更新，而较少更新的参数会有较大的学习率，鼓励它们继续更新。

AdaGrad和前面的SGD最大的不同就是他的learing_rate会根据当前的梯度大小来调整，而SGD的learing_rate是不变的。

但是这个方法也有问题就是

学习率过早衰减：由于 AdaGrad 是基于梯度的平方累积来调整学习率的，这意味着随着训练的进行，学习率会单调递减，最终可能导致学习率变得非常小，从而停止更新。特别是在训练的后期，这可能会影响模型的收敛性，导致训练停滞。
没有长时间有效的学习率：AdaGrad 的自适应机制通常会导致学习率在训练过程中迅速下降，尤其是在处理高频特征时，这可能会导致无法进一步优化模型。

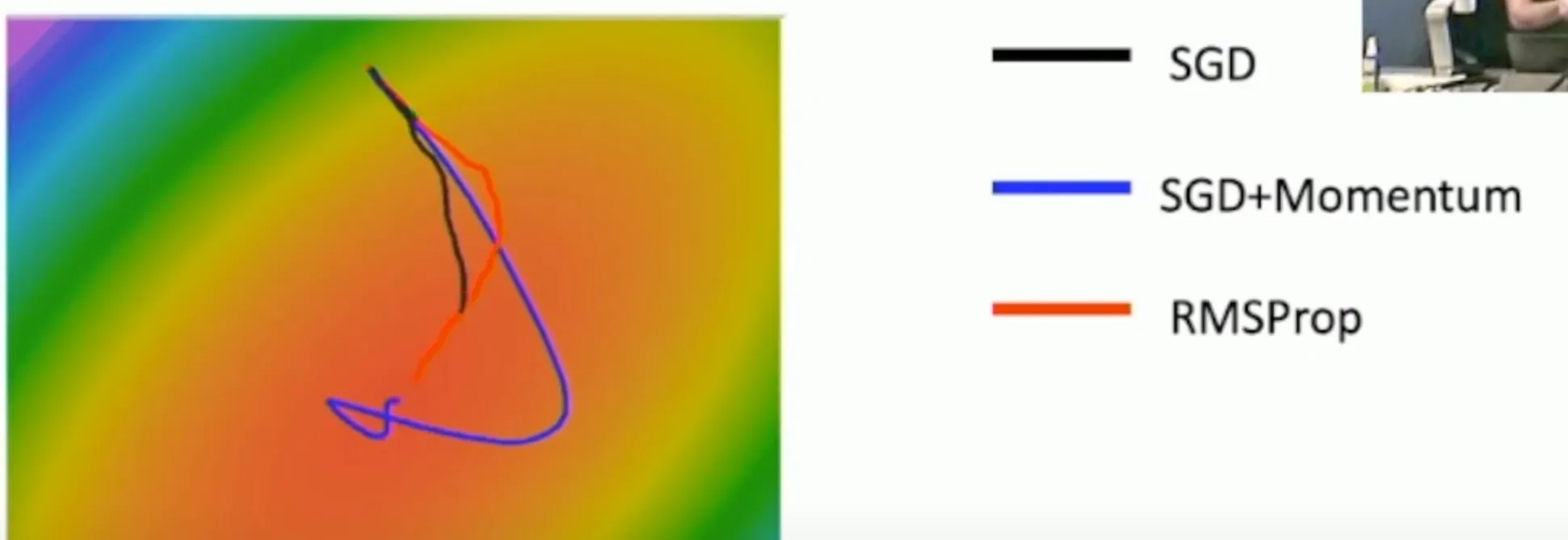
所以就有RMSProp

grad_squared = 0
for t in range(num_steps):
  dw = compute_gradient(w)
  grad_squared += decay_rate * grad_squared + (1 - decay_rate) * dw * dw
  w -= learing_rate * dw / (grad_squared.sqrt() + 1e-7)

python

这种办法可以避免grad_squared在不断的增大，导致学习率的衰减过早所以可以看到这种办法可以避免SGD+Momentum的过度更新

alt text

Adam：RMSProp+Momentum#

这种算法就将上面的两种算法结合

moment1 = 0
moment2 = 0
for t in range(1,num_steps + 1):
  dw = compute_gradient(w)
  moment1 = beta1 * moment1 + (1 - beta1) * dw
  moment2 = beta2 * moment2 + (1 - beta2) * dw * dw
  w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)

python

但是这个算法又有个问题就是如果一开始 t = 0，然后beta2=0.999/一个趋近于1的数，那么在一开始的时候，learing_rate就会变得非常大，意味着我们在一开始就迈一个很大的步伐

所以改进版就是

moment1 = 0
moment2 = 0
for t in range(1,num_steps + 1):
  dw = compute_gradient(w)
  moment1 = beta1 * moment1 + (1 - beta1) * dw
  moment2 = beta2 * moment2 + (1 - beta2) * dw * dw
  moment1_unbias = moment1 / (1 - beta1 ** t)
  moment2_unbias = moment2 / (1 - beta2 ** t)
  w -= learning_rate * moment1_unbias / (moment2_unbias.sqrt() + 1e-7)

python