MICE + Rubin's Rule

前言#

最近遇到了数据缺失需要填充的问题，一开始我以为数据填充没有什么，想法就是按照简单的来，用众数，中位数，平均数或平均数来填就行了。但是没想到这还是一个比较活跃的研究方向。于是记录一下。

概况#

根据Rubin 1976 提出的分类，数据缺失一般分为三种情况：

MCAR（Missing Completely At Random）完全随机缺失
缺失与任何变量都无关，例如系统崩溃导致某些记录丢失。
MAR（Missing At Random）随机缺失
缺失依赖于其他观测到的变量，例如收入字段缺失，但缺失概率和受教育程度有关。
MNAR（Missing Not At Random）非随机缺失
缺失依赖于未观测到的自身变量，例如重病患者可能不填写健康问卷。

常见处理方法及适用情况

方法	适用场景	特点
删除缺失值	缺失样本很少、MCAR	简单粗暴，可能丢失重要信息
均值/中位数/众数填充	连续/类别变量、近似MCAR或MAR	简单有效，但可能引入偏差
KNN 填充	缺失值不是太多，数据分布规律明显	保留一定相似性，但计算成本高
多重插补（MICE）	MAR，且需要保持估计的不确定性	当前主流方法之一，适合科研应用
回归填充	缺失变量和其他变量关系强	可以精准填补，但风险是过拟合
自编码器/深度学习填充	大量数据缺失或复杂关系	在图像/表格数据中表现较好，但难以解释
模型内处理	如 XGBoost、LightGBM 支持缺失值	不需要额外处理，但可能影响解释性

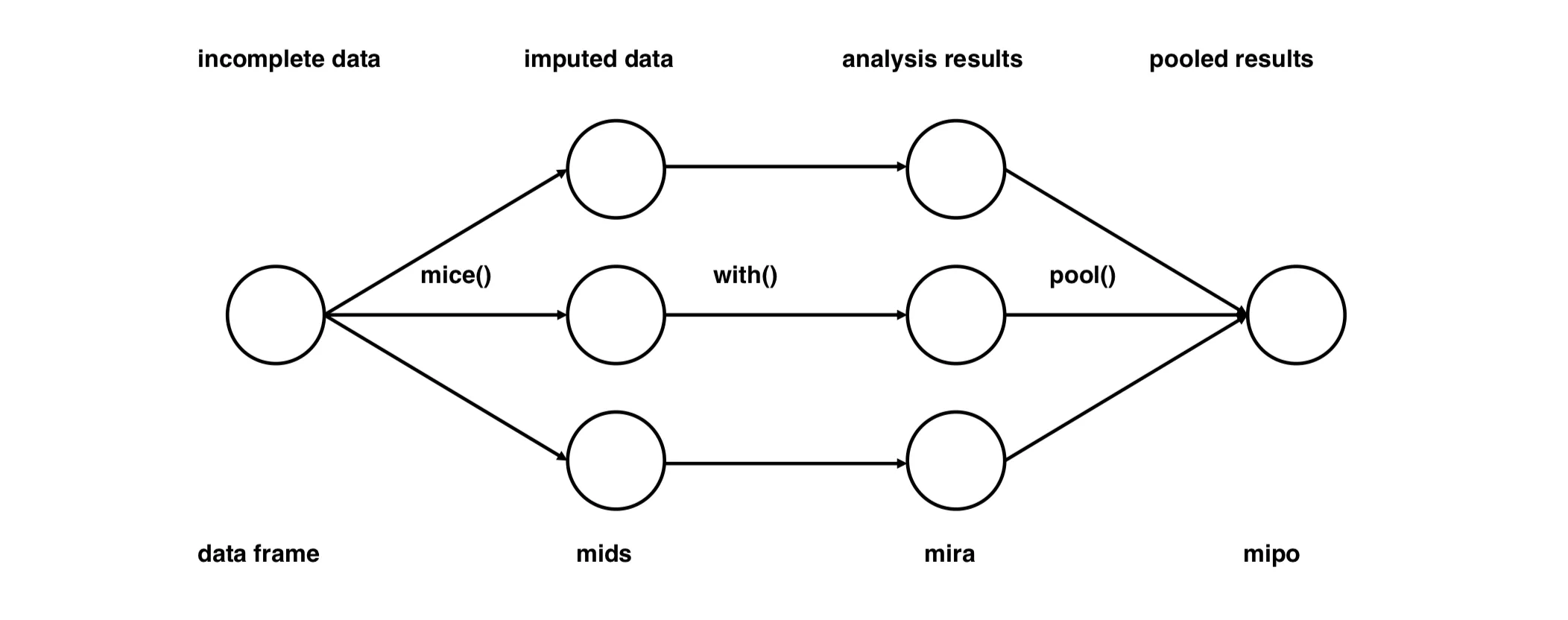
然后统计界可能最认可就是多重插补（Multiple Imputation），下面讲一下多重插补的比较经典的方法MICE（Multivariate Imputation by Chained Equations）。

MICE#

第一步：初始填补#

将有缺失的列先用一个初始值（比如均值、中位数、回归预测等）填上，使得整张表没有缺失值。

第二步：循环每一列（有缺失）进行建模（关键）#

对每一列 $X_j$ $X_{j}$ 有缺失的变量：
1. 把这一列作为目标变量 y；
2. 其余所有列作为特征变量 X；
3. 只用那些在 $X_j$ 上有观测值的行进行训练（因为 y 不能是 NaN）；
4. 用这个模型去预测 $X_j$ 上原来为缺失值的地方；
5. 用预测值填补这些缺失；
6. 然后进入下一列，重复这个过程。

第三步：迭代多轮更新#

上面这一过程会 循环进行多轮（如 10 次）：
- 每轮都重新建模、填补；
- 因为每轮填补后的数据更完整，所以后续预测也可能更准确。

第四步：多重插补（Multiple Imputation）#

上面步骤完成的是一次插补（single imputation）；
为了反映不确定性，MICE 会做 m 次独立的插补（每次加入随机性）：
- 用不同的 random_state 和 sample_posterior=True；
- 得到 m 组完整的数据集。

Rubin’s Rule#

这个衡量的是你的填补的结果的好坏

coef （平均系数）#

\bar{\beta} = \frac{1}{m} \sum_{i=1}^{m} \beta_i

它反映了变量对目标的平均影响程度。

当你用填充过后的数据进行一次回归预测的时候，你就得到每个特征对应的回归系数。比如

视力预测=0.8+(−0.02)⋅年龄+0.5⋅曲率+0.3⋅眼轴

0.3,0.5这些就是对应特征的回归系数。然后因为我们进行了m次插补，每次的数据不同，每次的回归系数也不一样。所以就平均一下每个特征的m次平均回归系数 $\bar{\beta}$

std_error（系数标准误）#

T = W + \left(1 + \frac{1}{m}\right)B

其中：

W：每个模型内部估计误差的平均（即原始的 bse**2）；
B：模型之间的回归系数差异（越大说明插补不确定性越大）；
T：总方差，反映了模型内部误差 + 插补不确定性；
std_error = sqrt(T)：总标准误，越大表示估计越不稳定。

W：Within-imputation variance（模型内部误差）#

每个插补数据集都会跑一次回归模型，每个模型都会给出自己的回归系数的标准误，比如第 iii 个模型中的第 j 个系数标准误为 $se_{ij}$ ，平方就是方差：

\mathrm{Var}(\beta_{ij})=se_{ij}^2

把每个模型里这个系数的标准误平方取平均，就是：

W_j=\frac{1}{m}\sum_{i=1}^mse_{ij}^2

这反映了：如果数据本来是完整的，我们模型预测值的方差是多少。

B：Between-imputation variance（模型间差异）#

你有 m 组回归系数 $\beta_{2j}, ..., \beta_{mj}$ ，表示多次插补后在同一个变量上的估计值。它们之间会有差异。所以我们计算这些系数之间的样本方差：

B_j = \frac{1}{m-1} \sum_{i=1}^{m} (\beta_{ij} - \bar{\beta_j})^2

为什么加上 $(1+\frac{1}{m})B$ ？#

这是 Rubin 提出的一个修正项，来源如下：

单纯的 B 是 样本方差；
要估计总体方差，需要一个偏差修正项；
$(1+\frac{1}{m})B$ 就是这个修正，考虑了：你只用了 m 个插补结果，样本不够多，所以要略放大不确定性。

t_value（t 统计量）#

t=\frac{\bar{\beta}}{\mathrm{std~error}}

用于做假设检验：

零假设 $H_0$ ：该变量对目标没有影响（即 $\beta = 0$ ）
如果 $|t|$ 很大（比如 > 2），说明这个变量对目标有显著影响。

前言#

概况#