这篇文章主要提出了一种像素级的自监督框架,感觉他摆脱了原本自监督正样本对和负样本对的思想,有点跳脱开来提出一种新的想法。原本的正负样本对属于二元对比学习,将正样本对拉近,然后将负样本对推开。但是论文指出这会有一个问题,over-dispersion(过度发散)。
模型在训练过程中,为了最大程度推开不同像素之间的特征,导致本来该相近、属于同一种结构/语义的像素(比如同一根血管、同一个区域),在特征空间里被拉得“彼此很远”,破坏了原有的空间或语义连续性。
本质上来说就是正样本对太少了,负样本对太多了。于是模型设法将除了正样本对其他的所有像素都当作负样本对,都推开。这样就会有问题,图像中有空间连续性和结构一致性,如果这样的话,正样本对周围原本具有连续性应该靠近的都被推开了,这样就会导致特征空间碎片化。
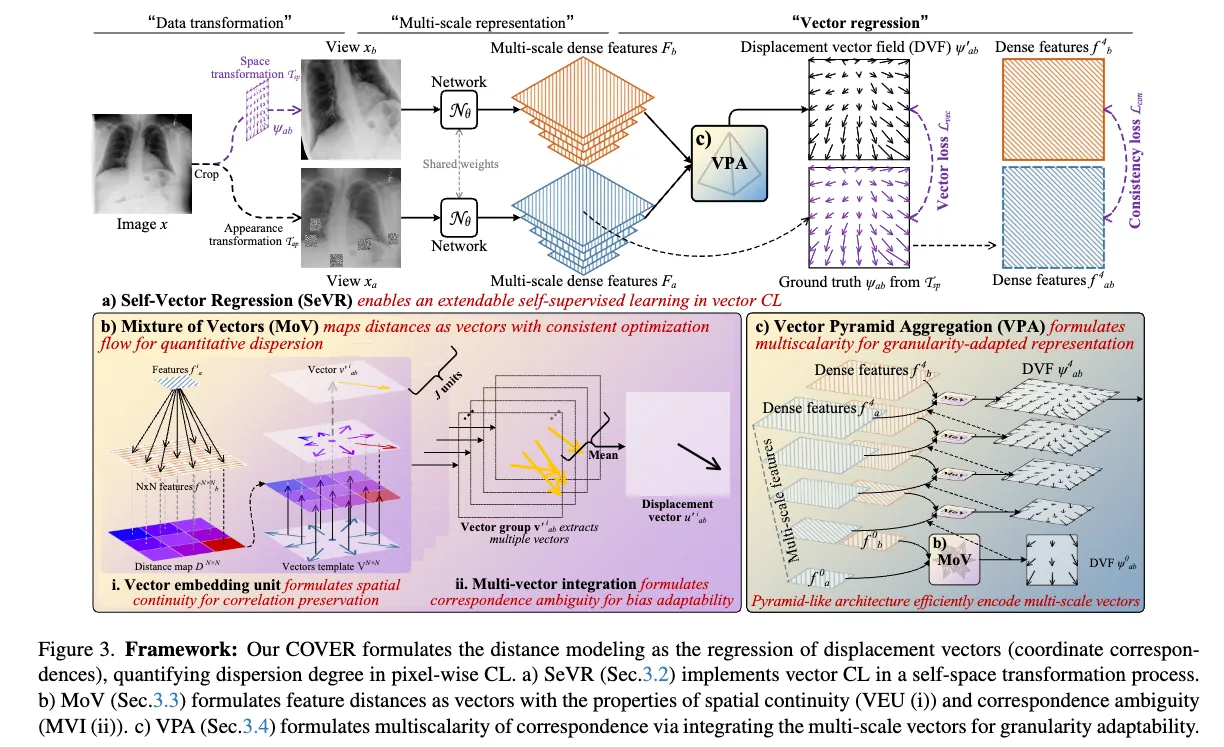
于是文章就提出一种思路,跳脱原本正负样本对的范式,他的想法是让模型学一个displacement vector field(DVF,位移矢量场)。想法就是我对图片进行空间变化,然后我让模型去预测这个矢量场,使得其中一张图片根据这个矢量场能够越来越接近另一个图片,预测的差异作为损失函数来训练模型。
Self-vector regression for extendable self-learning(SeVR)#
一开始的流程就是我从数据集中x∼D选一张图片。然后选两个图片增强方式,一个是颜色t∼Tap,另一个是空间ψab∼Tsp 。然后处理之后得到两张图xa=t(x),xb=ψab(x) 。经过同一个backbone提取特征之后,Fa={fal}l=0L=Nθ(xa) ,Fb={fbl}l=0L=Nθ(xb) 。他的想法就是我用经过空间增强后,我可以的到他的DVF,我用这个DVF作为ground truth ψabi,然后我用进行颜色增强的图片来预测这个DVF。想法就是我提取出特征向量之后,比较这两个图片的差异,然后为根据每一个像素转化成矢量。这就很神奇了,两个图片的差异或相似怎么得到一个矢量呢,后面会讲。
一部分的损失函数就是
Lvec(ψab,ψab′,ϵab)=i∈{ϵab=1}∑∣ψabi−ψab′i∣
其中ϵab=1 表示图像增强之后重叠有效的像素,一个mask。还有另一部分一致性损失
Lcon(fab4,fb4,ϵab)=−i∈{ϵab=1}∑∣∣fab4,i∣∣∣∣fb4,i∣∣fab4,i⋅fb4,i
其中fab4=ψab(fa4)
一致性损失也是很常见的概念,思想就是不管你对一幅图像做了什么变换(裁剪、旋转、空间扰动等),同一位置(或变换后位置)对应的像素/patch/区域,其表征特征应该不变或者尽可能相似。
文中意思就是我图a提取出来的特征fa4 经过ground truth的DVF处理之后fab4=ψab(fa4),他和图b的语义信息应该一样。计算他们的余弦相似度,然后作为损失函数。然后还有奇怪的地方在于fa4 这个4是什么意思,后面会讲。
所以总的就是LCOVER=Lcon+Lvec
Mixture of vectors with consistent optimization flow(MoV)#
Vector embedding unit (VEU)#
这里就是具体讲怎么从特征图到向量。
我们遍历图片中的所有像素,对于每一个像素,我们在另一张图上的相同位置取一个N×N的领域,然后我们用这个像素的特征向量去和这个领域里的特征向量做点积得到相似度矩阵,然后你用
这个和一个向量模版V去计算加权平均,得到最终这个像素的偏移矢量。以此类推,当遍历完一整个矩阵的时候最后得到DVF。
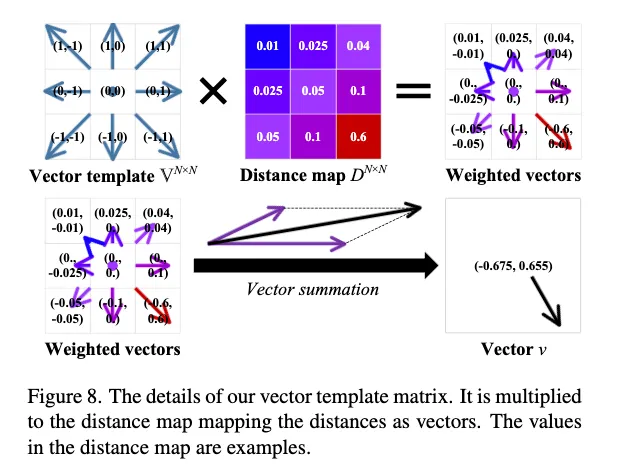 公式就是
公式就是
vab′i=U(fai,fbN×N)=softmax(τfaifbTN×N)VN×N
Multi-vector integration (MVI)#
这一段的目的就是我并没有直接处理整个特征向量,而是我讲他分割成 j 个组(小向量),然后每组跑一遍VEU,最后取平均。
u′=J1j=0∑Jv′j
为什么要多此一举呢,论文中解释由于语义连续性和特征多样性,像素的空间对应可能本身就是模糊/歧义/多样的,因此需要用多组特征分别“关注不同语义属性”给出多向量预测,再做融合。
Vector pyramid aggregation adapts granularity#
论文并没有只用一层的特征向量,他利用了backbone中的多层特征向量,从最顶层的特征向量开始逐步往下。
具体而言,例如
ψab′1=M(ψab′0(fa1),fb1)⨀ψab′0
我得到第0层的DVF ψab′0 然后我用这个去处理图a的第1层特征,然后我用处理后的特征向量来进行MoV,最后得到该层的初步DVF,然后再和前一层的DVF ψab′0 进行融合操作,最后得到这一层的DVF,以此类推,一直到最底层,精度越来越高。最终得到最后的DVF。
ψab′=V(Fa,Fb)=H({ψab′l}l=0L), whereψab′0=M(fa0,fb0)ψab′l=M(ψab′l−1(fal),fbl)⨀ψab′l−1,l=1,2,...,L−1,
那融合操作⨀ 是什么呢
ψab′1⨀ψab′0=ψab′1+Space alignmentψab′1(2∗IH×W(ψab′0))Scale alignmentVector fusion
(1) Scale alignment(尺度对齐)
- 把“上级层”(比如第 0 层)的 DVF 用双线性插值(bilinear interpolation)上采样到“下级层”——也就是让低分辨率的 DVF(向量场)和当前所处理的高分辨率 DVF 大小一致。
- 然后把所有向量的数值“放大一倍”(乘 2,或按比例缩放),这样空间单位也对齐到高分辨率那一层的格点范围。
(2) Space alignment(空间对齐)
- 即便分辨率对齐后,由于像素格点的排列逻辑不同,还要进一步对中心坐标调整(align),确保两个层级上每个像素/向量的几何对应关系完全对齐。
- 这些操作保证原本低分辨率的空间位移场被“正确映射”到高分辨率的坐标系。
(3) Vector fusion(向量融合)
- 最后把对齐好的两个层级的 DVF 逐元素相加,就得到了融合后的新一层 DVF。
- 直观上,就是“高分辨率细节+低分辨率全局趋势”既有整体又有细节的空间配准效果。
于是乎我们就得到了最后的DVF。



 公式就是
公式就是