
3D proxy task NeurIPS 2020 论文笔记
3D Self-Supervised Methods for Medical Imaging
前言#
 这篇文章的主要贡献就是提出3D领域的5个proxy task(代理任务),然后通过这些任务帮助预训练模型能更好的理解。
这篇文章的主要贡献就是提出3D领域的5个proxy task(代理任务),然后通过这些任务帮助预训练模型能更好的理解。
那为什么作者要以医学图像来作为背景呢,而不是传统的3D图像呢,因为医学影像3D数据的应用需求和挑战非常突出。 医学图像领域(如MRI、CT等)天生就是三维数据,且“人工标注难、标注昂贵、数据隐私敏感、样本规模有限”这些问题尤为严重。当然医学图像只是背景,本质上这些都可以迁移到任何3D图像领域里。
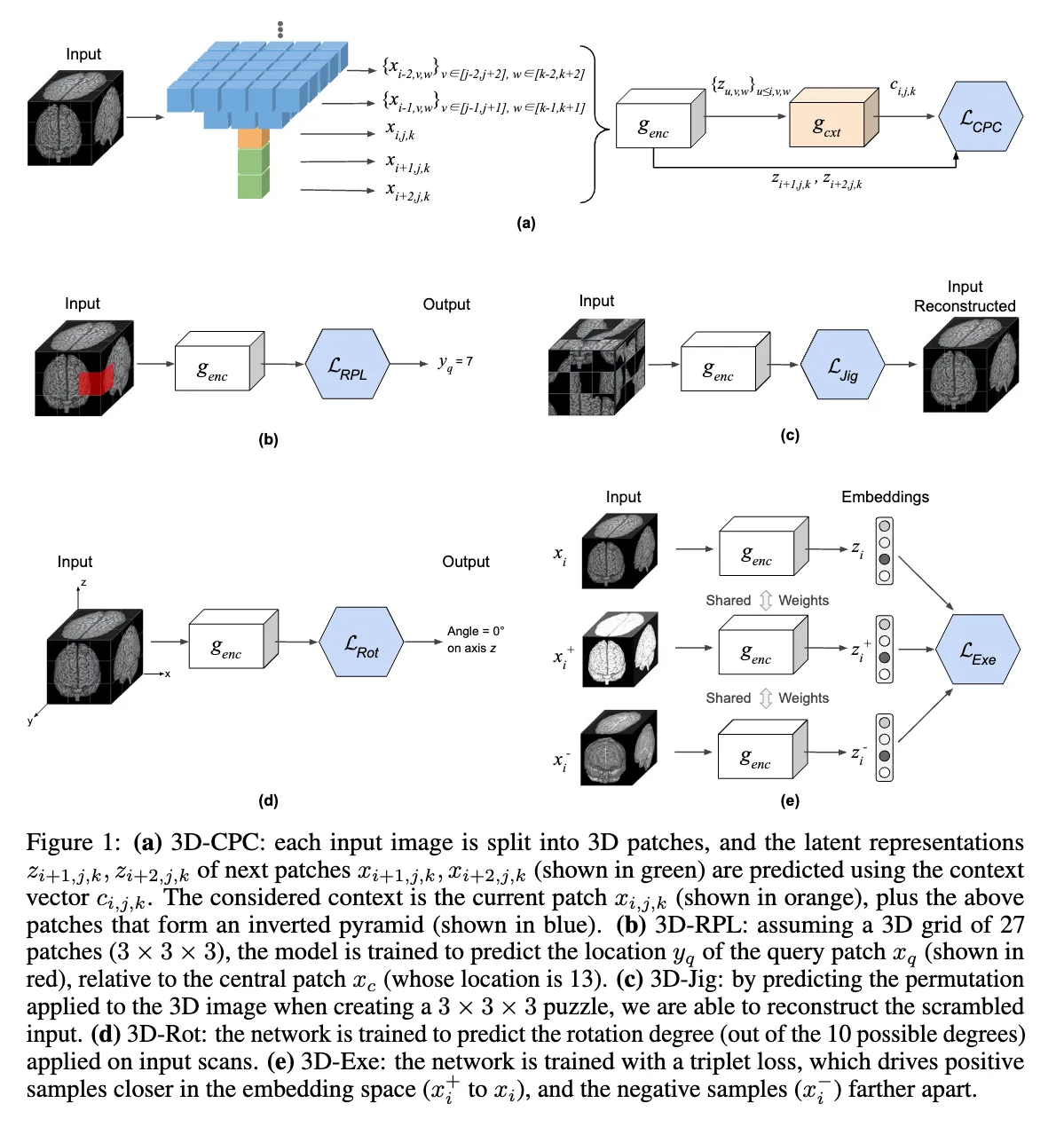
3D Contrastive Predictive Coding (3D-CPC)#
CPC是2018年就提出来的一个自监督学习方法,一开始是处理声音的,后续用到了2D图像领域,然后也影响了很多后来的自监督方法比如SimCLR,他的损失函数就是从这里提取灵感的。
一开始的CPC:
原始输入序列 被一个编码器 映射成潜在表示:
这些 是低维、压缩过的信息,代表输入的潜在特征。 上下文建模 使用一个自回归模型(如 GRU 或 Transformer)来聚合前面的信息形成上下文向量:
这个 表示“看到前 t 个输入后的理解”。 预测未来潜在表示 CPC 的目标不是直接预测未来的原始输入,而是预测未来的潜在表示 (通常 ):
然后,用一个 对比损失(InfoNCE) 来让预测的 和真实的 尽可能接近,并和其他负样本区分开来。 InfoNCE 损失 在每一个时间点 ,我们尝试从一堆样本(一个正样本,多个负样本)中分辨出哪一个是正确的 :
- 是正样本(未来的真实潜在表示)
- 是一组正负样本
- 是学习得到的变换矩阵
- 是上下文向量
本文提出的3D CPC:
先将3D图片分成同等大小,且有重叠的patch ,然后用encoder网络将它转化成latent representation(潜在表示) ,然后用另一个网络提取上文的信息 这个公式的意思就是第 i 层及其以前的所有块,按照倒金字塔来取,(可以看上面的图)用一个网络提取出信息来。没有全部取而是按照倒金字塔取的目的就是为了节省算力。
论文里面没有写,但实际上应该还有一个小的预测网络 ,用来预测下一个patch的特征向量。
损失函数长这样
但是有个很奇怪的点在于他的分母的求和为什么在exp的里面,而不是外面,常见的应该是在外面,不知道是不是笔误。
Relative 3D patch location (3D-RPL)#
这个任务就是将3D图片分为多块,然后取一个作为中间块,然后随机选一个块,预测他和中心块的相对位置。然后用预测结果分布和one hot的真实结果做交叉熵,然后多次预测求和。
这个公式其实跳了一下,对于第K个查询,他的交叉熵是
但是由于真实结果是one hot,所以这个只有一项,然后再求和一下多次查询求和,就是论文里的公式
3D Jigsaw puzzle Solving (3D-Jig)#
这个任务更像是进阶版的RPL,我们还是将3D图像分割成多个n*n*n个不重叠的块,然后总共有 种排列方式,然后我们选取其中的P种,然后随机从这P种里面挑一个打乱,然后让模型预测排列方式的概率分布,然后和one hot真实排列进行交叉熵计算。
值得注意的是,为什么我们不采用全部的 种排列方式,原因就是- 全部排列数太多(指数级增长),模型很难“记住”或判别。而且类别太多不仅带来巨大的参数和计算,最终训练时大多数类别都只出现一次,极其疏稀,不利于收敛。所以我们选P种,而且这P种使用最大化汉明距离(Hamming distance)得来的。
汉明距离衡量两组排列之间有多少位置不同(比如abcd和abdc,距离为1)。最大化汉明距离采样的目标是: 选择的每两个排列应尽可能多地不一样。这样做有几个好处:
- 每个类别之间显著不同,模型必须捕捉全局空间关系,不能偷懒记“细节小调整”。
- 提高了任务判别难度和特征鲁棒性。
- 减少类别混淆和标签不确定性。
3D Rotation prediction (3D-Rot)#
这个任务就是预测旋转了多少的角度,让3D图片沿着x,y,z三个坐标轴旋转,每个坐标轴可以旋转 ,然后论文里只考虑单独轴的旋转,不考虑组合旋转,所以总共有12种旋转方式。然后有3种是相同的(每个轴旋转0度),所以总共保留10种。还是预测旋转分布以及one hot的交叉熵。
3D Exemplar networks (3D-Exe)#
这个任务就是对图片进行不同的处理(比如随机翻转,随机旋转,随机亮度/对比度变化,缩放),然后对同一张图片的处理看作是正样本对,其他图片的处理看作负样本对。然后可以用交叉熵来作为损失函数。但是交叉熵的话,计算量就非常大,于是作者用了triplet loss。
D是欧氏距离(L2范数)。意思就是将图片x以及他对应的处理后的图片进行编码后得到z,然后他想让 之间的距离大于 且如果大于的距离大于的话,损失就为0。